【摘要】：图2.5.7多缝的夫琅和费衍射强度分布当干涉因子中分母为零时，分子也变为零，按洛比达法则可求得这时干涉因子取极大值N2，由此可得上式即是以空间频率fx表示的衍射强度取极大值所在的位置，称为多缝的傅里叶谱。
设此多缝由N个全同的狭缝构成，如图2.5.6所示，其透过率函数为
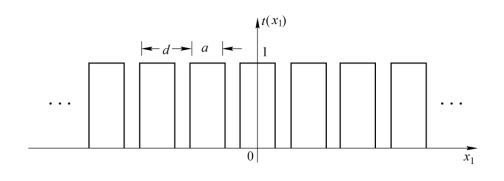
图2.5.6 多缝的透过率
①为简化计算，本题只讨论了图2.5.6中沿x1轴正方向各缝的衍射，沿x1轴负方向的衍射，也可类似计算。
式中，a为缝的宽度，d为各缝间的间距。当用单位振幅的单色平面波垂直照明时，其衍射光场分布为
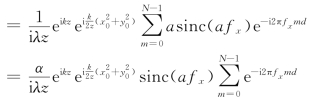
上式归结为求公比为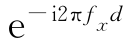
的等比级数的前N项和，其中
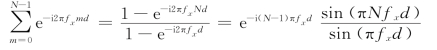
故得(www.xing528.com)
衍射光强分布为
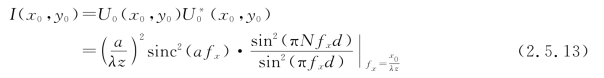
与式（2.5.3）比较可知，上式中的因子sinc2（afx）对应于单缝的衍射，而
代表各缝间多光束的干涉。因此，多缝的夫琅和费衍射花样是多光束干涉经单缝衍射调制后的结果，如图2.5.7所示。
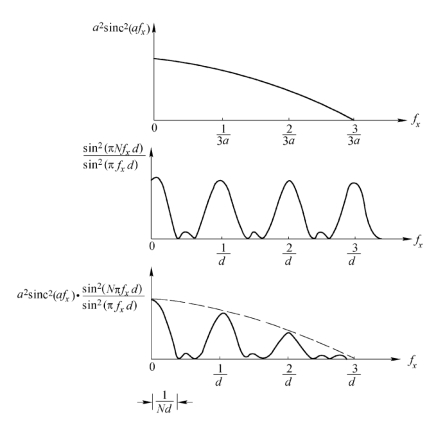
图2.5.7 多缝的夫琅和费衍射强度分布（d=3a）
当干涉因子中分母为零（即πfxd=mπ）时，分子也变为零，按洛比达法则可求得这时干涉因子取极大值N2，由此可得
上式即是以空间频率fx表示的衍射强度取极大值所在的位置，称为多缝（即线光栅）的傅里叶谱。
称为光栅沿x0方向的空间频率，又称为傅里叶谱的基频。d称为光栅沿x0方向的空间周期，又称光栅常数（Grating Constant）。
当干涉因子中的分子为零、分母不为零时，便得到衍射光强度的极小值。某一主极大相邻的两极小值间的空间频率宽度Δfx称为条纹主极大宽度，由πNfxd=±π求得Δfx=
。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
