菲涅耳近似在信息光学中的应用

由图2.4.1知，r01可表示成

按照下列公式对根号作二项式展开：

得到

由于只考虑z轴附近的区域，有z≫|x0-x1|2及z≫|y0-y1|2，故上式右端可只取前两项，则得

上式称为菲涅耳近似（Fresnel Approximation）。这个近似式成立的区域称为菲涅耳衍射区。

将式（2.4.5）代入式（2.4.2）得

上式称为菲涅耳衍射公式。现在对这个公式做如下讨论：

（1）近似程度估算

在导出衍射公式（2.4.6）时，略去了式（2.4.4）中的高次项，为了避免由此而导致明显的位相误差，则要求

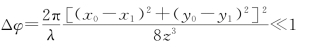
若允许（x0，y0）取观察区域内任何值，（x1，y1）取衍射孔径内任何值，则要求当[（x0-x1）2+（y0-y1）2]2取最大值时，Δφ仍远小于1个弧度，即(www.xing528.com)

当满足上式时，公式（2.4.6）肯定成立。但上式并不是菲涅耳近似的必要条件，而只是一个充分条件。事实上，要使菲涅耳近似成立，只要求展开式（2.4.4）中的高阶项不改变积分式（2.4.2）之值就行。由于k值很大，从而值也很大，故只要式（2.4.6）中的子波源坐标（x1，y1）与观察点坐标（x0，y0）有一定差异，其二次位相因子就将振荡很大，以致对积分的主要贡献仅仅来自（x0=x1，y0=y1）附近的点，那里的位相变化速度最小。在这些“稳相”点附近，次高阶位相项的大小往往可以完全忽略。在一般问题中，菲涅耳近似是很容易实现的。

（2）菲涅耳衍射的卷积表示

如果把衍射公式（2.4.6）写成叠加积分式（2.2.24）的形式，则显然有

上式称为菲涅耳衍射的卷积积分表达式。它表明：如果把菲涅耳衍射过程看作一个系统，则这个系统等效于一个线性空间不变系统，从而这种衍射过程必然存在一个相应的传递函数。根据2.3节的讨论，一般衍射过程的传递函数可由式（2.3.5）表示。对该式取菲涅耳近似可得

式中，eikz代表总体的位相延迟，这是任何空间频率成分在传播过距离z后都要产生的；而代表和空间频率平方有关的位相“色散”。

（3）菲涅耳衍射的傅里叶变换关系

将衍射公式（2.4.6）被积函数指数中的二项式展开，得到

令，则上式变为

上式可看作是傅里叶变换形式的菲涅耳衍射公式，亦即菲涅耳衍射可看成是乘积的傅里叶变换。稍后将会看到，在某些问题中，例如，当照明衍射屏的是会聚球面波时，U1（x1，y1）中将包含关于（x1，y1）的二次位相因子，在一定条件下可以与相消，使式（2.4.11）直接变成傅里叶变换形式，从而使菲涅耳衍射的计算得以简化。许多光学仪器像面上的衍射均属于这种情况。