信息光学理论应用：衍射规律频域描述

如图2.3.1所示，设有一单色光波沿z轴方向投射到衍射屏上，衍射屏后表面上的场用U（x，y，0）表示，观察屏上P0点的场记为U（x，y，z）。为了描述方便起见，在观察屏和衍射屏上都暂时采用同一种坐标系。又设G0（fx，fy）和Gz（fx，fy）分别代表U（x，y，0）和U（x，y，z）的频谱函数，根据傅里叶变换定义，有

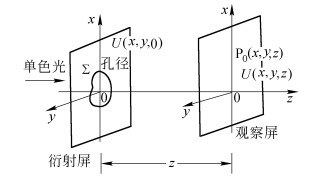
图2.3.1　计算角谱用的坐标系

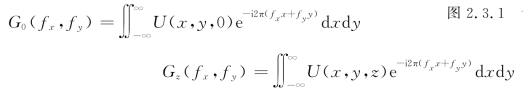
并且有

上式把U（x，y，z）分解成各种空间频率（fx，fy）的指数基元的集合，每个基元的权重密度为Gz（fx，fy）。前面已指出，频率为（fx，fy）的指数基元相当于以方向余弦cosα=λfx，cosβ=λfy和传播的平面波，这个平面波分量的复振幅就是Gz（fx，fy）dfxdfy在处的所求值。由于这个缘故，函数Gz（fx，fy）=称为扰动U（x，y，z）的角谱（Angular Spectrum）。同样，称为U（x，y，0）的角谱。另外，由于在所有无源点上，U（x，y，z）必须满足亥姆霍兹方程（2.2.4），故将式（2.3.1）代入式（2.2.4），并改变积分与微分的顺序，有

在对上式进行微分运算时，注意到Gz（fx，fy）在空域坐标系中仅仅是z的函数，经直接运算后，得到下列微分方程：

上式是一个二阶线性齐次常微分方程，其特征根r为

上式中取“+”号得到方程（2.3.2）的一个基本解（另一个解是倒退波，此处不予讨论）是

式中，A是积分常数，由初始条件决定。初始条件是：z=0时，A=G0（fx，fy）。最后得到方程（2.3.2）的一个基本解为

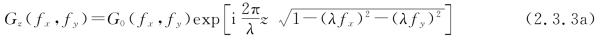(www.xing528.com)

或

公式（2.3.3a）和（2.3.3b）表现了频谱函数Gz（fx，fy）与G0（fx，fy）之间的联系，因此它就是衍射规律的频域表达式。该式表明，可以用频谱的语言来描述光波的衍射过程。光波从z=0的平面传播到z=z的平面时，相应的频谱函数由G0（fx，fy）转换成了Gz（fx，fy），并且P0点的频谱函数Gz（fx，fy）仍可用P1点处的频谱函数G0（fx，fy）表示，仅多了一个位相因子。因此，公式（2.3.3）又表示了角谱的传播。

下面对公式（2.3.3）的指数因子再做进一步讨论。

①(λfx)2+(λfy)2＜1

这时，频率为（fx，fy）的指数基元相当于方向余弦是cosα=λfx和cosβ=λfy的平面波，它在传播过程中既不会改变方向，也不会改变振幅，只是改变了不同平面上复振幅的相对位相。由于方向余弦必须满足cos2α+cos2β+cos2γ=1，故只有（fx，fy）满足（λfx）2+（λfy）2＜1的指数基元，才真正对应于沿空间某一确定方向传播的平面波。

②(λfx)2+(λfy)2＞1

这时，公式（2.3.3）中的平方根变为虚数，遂可写成

其中，μ是正实数，即

很显然，对于一切满足（λfx）2+（λfy）2＞1的（fx，fy），所对应的波动分量将随z的增加按指数e-μz急速衰减，在几个波长距离内很快衰减到零。这些角谱分量称为隐逝波（Evanescent Wave）。这些隐逝波并不把能量从孔径带走。

③(λfx)2+(λfy)2=1

这时，cosγ=0，即γ=90°。该频率对应的指数基元相当于传播方向垂直于z轴的平面波，它在z轴方向的净能流为零。