信息光学理论与应用：基尔霍夫衍射公式解析

现在应用基尔霍夫积分定理来考察无限大不透明屏上的一个小孔所引起的衍射问题。如图2.2.2所示，假定一个光扰动从左面投射到屏幕和孔径上，要计算孔径后面一点P0处的光扰动。

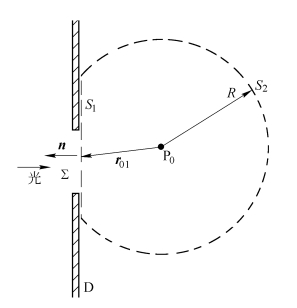
图2.2.2　平面屏衍射的基尔霍夫理论推导

选择的封闭面由两部分组成，即由正好位于孔径∑后且紧靠屏幕的平面S1与一个半径为R、中心在观察点P0的大球形罩S2组成。显然，只要球面半径R比P0点到屏的距离长，球面S2总会与无限大屏D相交，构成平面S1。遂由积分定理（2.2.11）有

其中，G仍由定义式（2.2.6）给定。

先看在S2面上的积分值：当R增大时，S2趋于一个大的半球壳，并且在S2面上有

于是，式（2.2.12）中S2面上的积分可化为

式中，Ω是S2对P0点所张的立体角，它是小于4π的一个常量。又由式（2.2.13）中第一个等式显见，|RG|=|eikR|=1，这个量在S2上是一致有界的。所以，只要满足下列条件：

(www.xing528.com)

则S2面上的整个积分将随着R趋于无穷大而消失。条件式（2.2.14）称为索末菲辐射条件（Sommerfeld Radiation Condition）。此条件是否被满足，必须对各种情况进行检验，但若扰动趋于零的速度至少像发散球面波一样快，则此条件满足。因为这时有，把它们代入式（2.2.14）便得

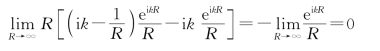
由于投射到孔径上的光扰动总由各个球面波或球面波的线性组合所构成，故可确信这个条件实际总会满足，于是S2面上的积分正好为零。

现在P0点的扰动可以只用紧靠屏幕后方的无穷大平面S1上的扰动及其法向导数表示，即

屏幕D上除了敞开着的孔径∑之外，其余部分是不透明的，所以从直观上看来，对积分式（2.2.15）的贡献应该主要来自S1面上位于孔径∑内的那些点。可以预期，被积函数在那里最大。因此，基尔霍夫采用了下述假设：①在孔径∑上，光场分布U及其导数与没有屏幕时完全相同；

②在S1面上位于屏幕几何阴影区内的那一部分上，光场分布U及其导数恒等于零。

这两条假设称为基尔霍夫边界条件（Kirchhoff’s Boundary Condition）。于是，式（2.2.15）简化为

上式与式（2.2.15）不同，它必须在基尔霍夫边界条件得到满足的前提下才成立。但是应该认识到，这两个边界条件中没有一条是严格成立的。首先，同时对光场及其法向导数施加了边界条件，这使得基尔霍夫衍射公式本身还存在着内在的不自洽性（Incompatibility）；其次，屏幕的存在必然会在一定程度上干扰孔径上的光场分布，并且屏幕后的阴影处光场也不可能完全为零，因为光场总是要扩展到屏幕后孔径区域之外几个光波长的距离。但是，如果孔径的线度比光波长大得多，或观察点离孔径∑较远，那么这些边缘上的精细效应尽可忽略不计，并且用这两个边界条件能得出与实验符合得很好的结果。

附带指出，选择换用别的格林函数，可以对基尔霍夫边界条件做进一步改善，从而消除衍射理论中的内在不自洽性。有关这方面的讨论留在本章习题中进行（见习题2.1，2.2）。