数学预备知识：信息光学理论与应用

在着手讨论衍射问题之前，首先介绍一些数学预备知识，以便为推导衍射公式打下基础。

1.亥姆霍兹方程

设用标量函数u（P，t）表示空间某点P在时刻t的光扰动，对于线偏振波的情形，可以认为这个函数代表电场强度。暂时先只限于讨论频率为ν的单色光波，则有

式中

称为光扰动的复振幅或相幅矢量（Phasor）。

u（P，t）在每一个无源点上必须满足标量波动方程：

式中，是拉普拉斯算子（Laplacian Operator），在直角坐标系中为

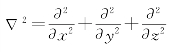
对于单色光波场，由于频率ν恒定，从而对时间的函数关系ei2πνt已经预先知道，故复振幅U（P）已足以描述空间某点的光扰动，它基本上包含了所需要的光波空间结构的信息。将式（2.2.1）代入式（2.2.3），可得复振幅必须满足的方程：

式中，k=，k称为波数（Wave Number）。式（2.2.4）称为亥姆霍兹方程（Helmholtz Equation）。对于在自由空间或均匀介质中传播的所有单色光扰动，其复振幅都必须满足这一方程。

2.格林定理

令U（P）和G（P）是空间位置坐标的两个任意复函数，S为包围空间某体积V的封闭曲面。若在S面内和S面上，U（P）和G（P）均单值连续，并且具有单值连续的一阶、二阶偏导数，则有

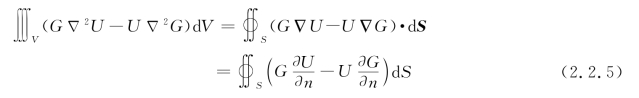
关系式（2.2.5）即称为格林定理（Green’s Theorem）。其中dS=ndS，n是面元dS上指向S外的法向单位矢量，表示在曲面S上每一点沿向外法线方向的偏导数。

格林定理的证明是比较简单的。由矢量分析中的高斯散度定理公式知，对于任一矢量场F，在任意体积V内其散度的体积分，等于V的闭合边界面S上该矢量场的面积分，即

现令，并利用矢量恒等式：

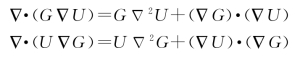
便可证明公式（2.2.5）。

格林定理是标量衍射理论的主要基础。但是，只有慎重地选择作为辅助函数的格林函数G和封闭曲面S后，才能将该定理直接应用到衍射问题上来。

3.基尔霍夫积分定理(www.xing528.com)

基尔霍夫衍射理论是建立在一个积分定理基础上的。这个积分定理把齐次波动方程在任意一点的解，用包围该点的任意封闭曲面上方程的解及其一阶导数之值表示出来。

令观察点为P0，并令S代表包围P0点的任一封闭曲面，如图2.2.1所示。问题是要用封闭曲面S上的光扰动值来表示在P0的光扰动。为此，首先将格林定理表达式作一些简化。令U（P）为单色光场的复振幅，并选择函数G（P）为由P0点向外发散的同频率的单位振幅的球面波（称为自由空间格林函数），即

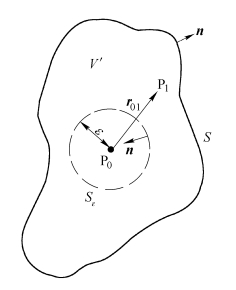
图2.2.1　积分曲面的选择

式中，r01表示从P0点指向P1点的矢量r01的长度。前面已指出，函数U（P）和G（P）及其一阶、二阶导数在被包围的体积V内必须是连续的，才能运用格林定理。但在P0点，G（P0）出现了不连续的情况。为了排除在P0点处的不连续性，可以P0点为球心，用半径为ε的小球面Sε嵌在P0点周围，然后应用格林定理。这时积分体积V′为介于S面和Sε面之间的那部分空间，面积分曲面是复合曲面S′=S+Sε。而在曲面S和Sε上的“外向”法线方向如图2.2.1所示。

在体积V′内，扰动G（P）只是一个向外扩展的球面波，它必然满足亥姆霍兹方程：

将式（2.2.4）和式（2.2.7）代入格林定理表达式（2.2.5）左端，得到

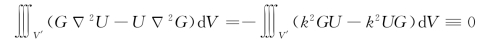
于是，格林定理（2.2.5）简化成

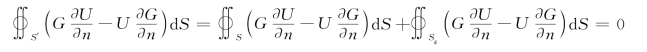
或

现在，再由上述简化的格林定理表达式导出基尔霍夫积分定理。对于在S上的任一点P1，有

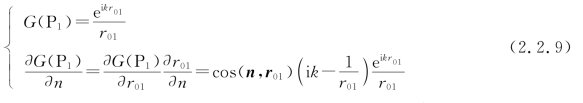
式中，cos（n，r01）代表外向法线n与由P0点至P1点的矢量r01之间夹角的余弦。

对于Sε上的P1点的特殊情况：r01=ε，则cos（n，r01）=-1，这时式（2.2.9）变为

令ε→0，则由U及其导数在P0点的连续性，利用微积分学里的中值定理，U和用P0点的值代替，而Sε=4πε2，便得

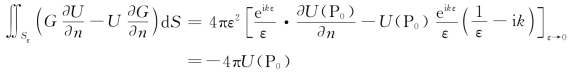
将上述结果代入式（2.2.8），得到

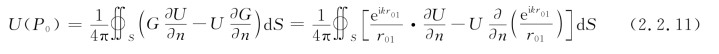
这个结果称为基尔霍夫积分定理（Kirchhoff’s Integral Theorem）。其意义是：衍射光场中任意点P0的复振幅分布U（P0）可以用包围P0点的任意封闭曲面S上各点的波动边界值U和求得。显然，这是一个根据边界值求解波动方程的问题。这一定理在标量衍射理论的发展中起着重要作用。公式中积分面的选取有着很大的灵活性，在求解具体问题时完全可以根据具体情况选择适当的封闭面，而使问题变得简单。