图像函数的采样表示法

采样过程在数学上是通过原函数与一个采样函数相乘来实现的。显然，对于图像函数f（x，y）来说，用它在（x，y）平面内的一个分立点集上的采样值阵列来表示往往是方便的，因此，比较理想的是采用二维梳状函数作为采样函数。从直观上能清楚看出，如果这些采样点间隔取得相当小时，那么可以说采样数据就很接近原图像函数的精确表示。

函数f（x，y）的采样由下式定义：

其中

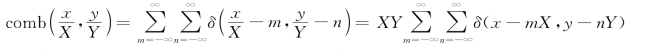
因此，采样值函数fS（x，y）由δ函数的阵列组成，各个δ函数之间的相互间隔在x方向上的宽度为X，而在y方向上的宽度为Y。

为了分析方便，可以研究fS（x，y）的频谱。应用卷积定理，由式（1.10.1）有

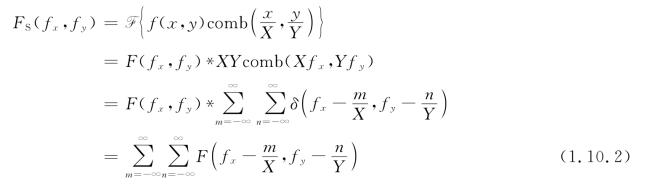(www.xing528.com)

上式表明，采样值函数的频谱由频率平面上无限重复的原函数的频谱所构成，形成排列有序的“频谱岛”，其重复间距分别为，如图1.10.1（a）所示。

从式（1.10.2）可以看出，如果令m=n=0，则FS（fx，fy）=F（fx，fy），即从采样值函数的周期性重复的频谱中可绝对准确地恢复出原函数的频谱。方法是让采样值函数的频谱FS（fx，fy）通过一个能够无畸变地传递式（1.10.2）中的m=n=0项，并同时能完全阻挡所有其他各项的线性滤波器。这样，在这个滤波器的输出端，就会得到原始函数f（x，y）的绝对准确的复现。

但是，从图1.10.1（a）可以看出，要能从采样值函数的周期性重复的频谱中恢复原函数的频谱，必须使各重复的频谱彼此分得开，为此，原函数的频谱宽度应是有限的。这样的函数称为带限函数（Bandlimited Function），其定义如下：

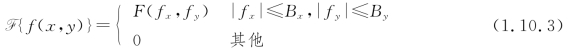
即要求f（x，y）的频谱只在频域中一个有限区域R内不为0。图1.10.1（b）表示某二维带限函数的频谱分布。

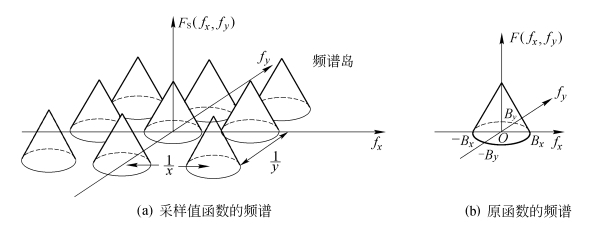
图1.10.1　函数的频谱