线性空间不变系统传递函数-信息光学理论与应用

线性系统中有一个重要的子类，即线性空间不变系统，它具有很特别的性质和重要应用。下面首先给出这种特殊线性系统的定义。

设线性系统对输入信号f1（x，y）和f2（x，y）分别产生输出信号g1（x，y）=S{f1（x，y）}和g2（x，y）=S{f2（x，y）}，若输入函数在空间发生了平移，且对任意复常数a1和a2，有

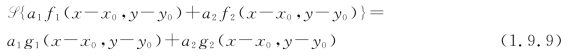
则称此系统为线性空间不变系统（Linear Space Invariant System，LSI）。上式表明：LSI系统对输入信号空间位置的平移所产生的唯一效应是：其输出信号也产生了同样的位置平移。

对于线性空间不变系统的含义，还可以结合一个理想成像系统来理解。设在此系统中，物函数f（x1，y1）对应像函数g（x2，y2），当物分布形式不变，仅在物平面上发生一位移，即f（x1，y1）变为f（x1-x0，y1-y0）时，对应的像函数形式不变，也只在像平面上有一个相应的位移，即g（x2，y2）变成了g（x2-Mx0，y2-My0），其中M代表成像系统的横向放大率，不失一般性可令M=1。按照LSI定义式（1.9.9）知，理想成像系统就是一个线性空间不变系统。空间不变特性是理想成像系统必备的。图1.9.2以一维形式表示了这一平移不变性质。

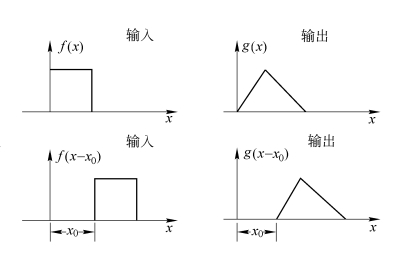
图1.9.2　LSI系统对一维函数的平移不变效应

线性空间不变系统具有一些重要的特性，现分析如下：

（1）脉冲响应具有比较简单的形式。在LSI系统中，其脉冲响应函数h（x2，y2；ξ，η）只依赖于坐标差（x2-ξ）和（y2-η），可以写成

即，当点光源在物场中移动时，其像斑只改变位置，而不改变其函数形式。这一特性称为等晕性（Isoplanatism）。当然，把实际的成像系统当作线性空间不变系统，只是一种理想化，事实上，由于实际成像系统存在像差，而像差大小与物点位置有关，故成像系统很少能在它的整个物场上是等晕的。但只要像差大小随物点位置的变化比较缓慢，往往有可能把物场分成许多小的等晕区（Isoplanatic Region），在每个这样的小区域中系统是近似空间不变的。为了完备地描写成像系统，应当给出适用于每个等晕区的脉冲响应。但是，如果所关心的那一部分物场相当小，通常只要考虑系统轴上的等晕区就够了。(www.xing528.com)

（2）叠加积分式（1.9.7）具有特别形式，即

上式表明，LSI系统的输出函数（像）可以表示为输入函数（物函数）与系统脉冲响应在输出平面上的一个二维卷积。这一特殊形式的叠加积分又称为卷积积分，我们在1.3节早已熟悉。由此可见，脉冲响应函数h完全描述了LSI系统的性态，故也称h为LSI系统输入-输出关系的空域描述。

（3）傅里叶变换形式特别简单。对式（1.9.11）进行傅里叶变换，并利用卷积定理得

式中

H（fx，fy）称为系统的传递函数（Transfer Function），它表示系统在频域中对信号的传递能力。

从式（1.9.11）和式（1.9.12）可以看到，用脉冲响应函数和传递函数来描述线性空间不变系统对输入函数的变换作用时，两种方法是等效的，只不过前者是在空域中描述，后者是在频域中描述。利用后一种方法时，可将求系统输出时需要的比较冗繁的卷积运算（1.9.11），变成更简单的一系列运算，即先作傅里叶变换，再将变换式相乘，最后进行傅里叶逆变换。从表面上看，这种方法包括正、反两次变换和一次乘积运算，似乎比前一种方法复杂、烦琐，然而事实并非如此，因为利用傅里叶变换的各种性质，常常可以使傅里叶变换、乘积和逆变换这些运算过程远比卷积运算方便，因此，从频域来考察线性空间不变系统，不仅具有重要的理论意义，还具有很高的实用价值。

当然，对频域中的这种描述只是对线性空间不变系统才成立。