【摘要】：由此可见，广义傅里叶变换就是极限意义下的普通傅里叶变换。因此，可采用同样的算符F{·}和F-1{·}表示广义傅里叶变换。广义傅里叶变换可以按照普通傅里叶变换相同的规则进行演算，二者之间的差别一般可以不计。为了说明广义傅里叶变换的计算，下面列举两个例子。求符号函数sgn的傅里叶变换。由式取极限得上式就是符号函数的广义傅里叶变换。
假定有一个函数序列gN（x，y），其中的每一个函数都存在傅里叶变换，对应的频谱函数为GN（fx，fy）。函数g（x，y）虽然不存在傅里叶变换，但g（x，y）却是gN（x，y）在N→∞时的极限，则定义N→∞时GN（fx，fy）的极限为g（x，y）的广义傅里叶变换（Generalized Fourier Transform）。由此可见，广义傅里叶变换就是极限意义下的普通傅里叶变换。因此，可采用同样的算符F{·}和F-1{·}表示广义傅里叶变换。
广义傅里叶变换可以按照普通傅里叶变换相同的规则进行演算，二者之间的差别一般可以不计。为了说明广义傅里叶变换的计算，下面列举两个例子。为简洁起见，这里只讨论一维情况，二维情况按可分离变量函数的变换求解。
【例1】求符号函数sgn（x）的傅里叶变换。
【解】计算过程可分为3个步骤。
（1）选择适当的函数序列。例如，取
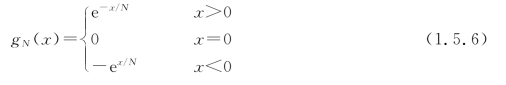
由式（1.1.7），显然有
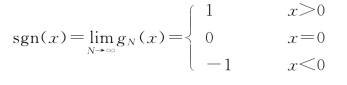
（2）求F{gN（x）}。
（3）求
。
由式（1.5.7）取极限得
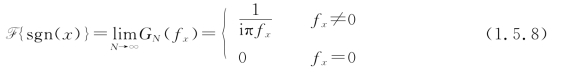
上式就是符号函数的广义傅里叶变换。
【例2】求δ（x）的傅里叶变换。(www.xing528.com)
【解】（1）选择适当的函数序列。
例如，从表1.2.1中选取
显然有
（2）求F{fN（x）}。
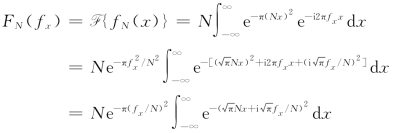
令
，并利用积分公式[2]，得
容易算得
（3）求
。
由上式取极限最后得
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
