信息光学理论与应用：卷积运算实例

由于卷积运算过程比较麻烦，初学者常感到难以操作，为此特列举几个运算示例。为了简洁起见，只讨论一维情形。

【例1】设有二函数，分别为

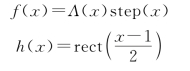
试求它们的卷积：g（x）=f（x）*h（x）。

【解】这两个函数对应的曲线如图1.3.3所示。按照前面介绍的卷积运算过程，首先将两个函数的自变量x换成积分变量ξ，接着将h（ξ）翻转成h（-ξ），再沿x轴将h（-ξ）平移x得到h（x-ξ），最后将两个函数进行乘积、积分。这里采用的图解分析将有助于确定卷积运算中的积分限。同时，根据x的可能取值范围，即x≤0、0＜x≤1、1＜x≤2、2＜x＜3和x≥3等几种情形，分别画出f（ξ）h（x-ξ）乘积曲线下的面积，如图1.3.4（a）～（h）中的阴影区域（重叠面积部分）所示。

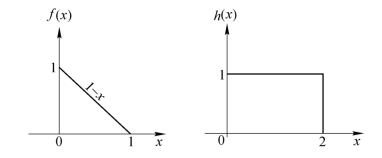
图1.3.3　例1中两个函数的图形

图1.3.4　例1一维卷积过程

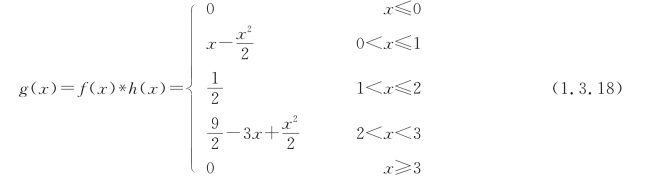
综合上述各式，可知所求二函数的卷积为根据上述计算结果画出了g（x）=f（x）*h（x）的完整曲线，如图1.3.4（i）所示。

【例2】求下面的卷积。

【解】由卷积定义式和矩形函数表达式，有

其中，rect经翻转并平移x后，有

(www.xing528.com)

由式（1.3.19）的积分限知，-2≤ξ≤0，再结合式（1.3.20）中矩形函数的表达式可以看出：当ξ=-2时，有-2≤x≤0；当ξ=0时，有0≤x≤2。故只有当-2≤x≤0和0≤x≤2时，函数乘积曲线下的积分面积不等于0，而当x超出上述界限时，积分面积都为0，如图1.3.5所示。

图1.3.5　例2卷积运算过程

遂有

故最后结果可表示成

其函数图形如图1.3.6所示。

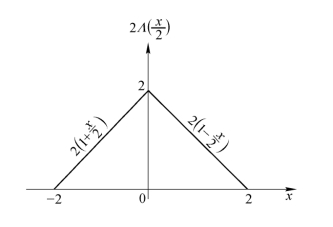
图1.3.6　例2卷积运算结果

【例3】求下面的卷积。

【解】由卷积定义式和梳状函数表达式，有

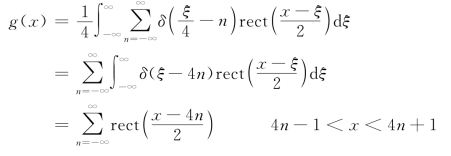
其函数图形如图1.3.7所示。该结果可用来表示罗奇（Ronchi）光栅的强度透过率。

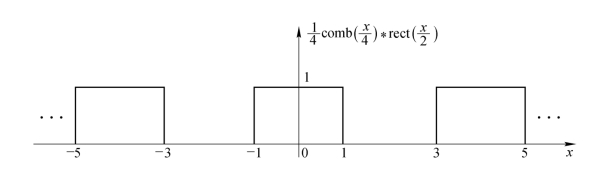
图1.3.7　例3卷积运算结果