函数在信息光学中的物理意义

δ函数常用来描述脉冲状态这类物理现象。时间变量的δ函数用来描写单位能量的瞬间电脉冲；空间变量的δ函数可以描写诸如单位质量的质点的质量密度，单位电量的点电荷的电荷密度，单位光通量的点光源的面发光度等。作为例子，考察平行光束通过透镜后会聚于焦点时的照度分布，如图1.2.3所示。图中，L是一个理想会聚透镜，平行光束通过透镜后会聚于焦点F′，在L与焦平面之间放置一个与透镜轴线垂直的屏P，假设透镜孔径的衍射可以忽略，这时屏上得到一个界限清晰的圆形亮斑，随着屏P向后焦面趋近，亮斑的直径越来越小，屏上的照度A（x，y）（投射到单位面积上的光通量）越来越大，在屏与后焦面完全重合，这种极限情况下，屏上F′点的照度已无法用普通函数来描述了，它在焦点处的值为无限大，在焦点以外为0。换言之，后焦面上的照度分布A（x，y）满足以下两个方程：

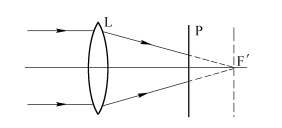
图1.2.3　用δ函数表示后焦面上的照度分布

(www.xing528.com)

如果将通过透镜的光通量归一化，则上式与式（1.2.1）相同，即后焦面上的照度分布可用δ（x，y）描述。类似地，也可分析由空间任一点P（ra）处的点光源所发出的面发光度La（r）（通过单位面积所传送的光通量）。当包围该点的封闭面无限缩小时，其面发光度达到无穷大，而总光通量是有限的，故有

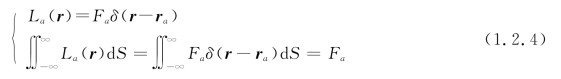
式中，Fa表示由点光源发出的全部光通量。所以，一般在光学中用δ（x-x0，y-y0）来直接表示平面上点（x0，y0）处的点光源。在一维情况下，δ（x-x0）表示在x=x0处的一个线光源（或无限细的狭缝光源）。