海南环岛高速铁路风荷载计算方法研究与应用

《建筑结构荷载规范》（GB 50009）、《轨道交通地面装置电力牵引架空接触网》（GB/T 32578）、《铁路电力牵引供电设计规范》（TB 10009）中均规定了建筑结构在风荷载作用下的计算方法，规范中规定的计算公式及各参数的含义如表7.1-1所示。

表7.1-1　风荷载计算公式及各参数含义

从上表可看出，规范对结构风荷载的计算方法基本一致，但是参数取值差异较大，同时该计算方法仅适用于正常工况情况下进行接触网结构设计时承载能力极限状态的风荷载计算。而海南岛地处我国台风高发地区，当发生台风时，接触网结构处于非工作状态，此时接触网结构仅需保证不破坏或倒塌，即当发生强台风时，接触网结构可不考虑安全系数，仅需进行强台风作用下的强度校验即可，校验公式如下：

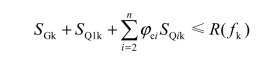
其中：SGk为恒载标准值；SQ1k为台风校核荷载标准值；　φci为第i个活载组合值系数；SQik为第i个活载标准值。

综上，对海南环岛接触网结构在强台风作用下进行设计时需按照极限状态法考虑接触网结构风荷载，同时还应按照历史记录的最大台风进行破坏校核，从而保证接触网结构在强台风下的安全性，因此需通过深入研究确定海南环岛风荷载计算方法中的各输入参数取值，为后一步的分析打下基础。

1.基本风速

关于基本风速在IEC 60826 A.4.2、《建筑结构荷载规范》（GB 50009）中有详细的规定，但二者有略有区别，现将二者规定对比如下：

（1）IEC 60826 A.4.2。

风的作用是以基本风速（离地 10 m 高、平均时距 10 min 的平均风速）来评价的。vR为重现期T年的基本风速（对于不同的可靠性等级1级、2级、3级，T 分别取 50 年、150 年、500 年）。通常，气象站（除那些沿海岸线或城市区域外）放置于B类地形。B类地形的基准风速为vRB。然而气象学的风速可能是在 x 类地形离地 10 m 高、平均时距 t 的速度vx，t（如果不是在离地 10 m 高测的数据，该数据应首先调整到10m高）。

图7.1-1为各种地面粗糙度类型下平均时距t下风速的关系vx，t/vx，10：

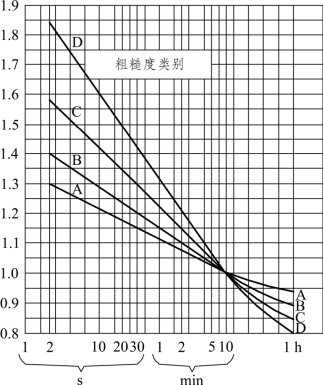
图7.1-1　不同时距风速关系

在仅有B类地形的基本设计风速vRB的情况下，其他地形基本风速vR可由公式vR=KRvRB确定，其中KR为粗糙度系数。

不同高度风速间的关系为：

不同地形：

其中：α对不同类别地形取值如表7.1-2。

表7.1-2　α的取值

注：在气象台站观测中，一般是取 2 min 的平均风速；自记仪器是取 10 min 的平均风速。

（2）《建筑结构荷载规范》（GB 50009）。

E.2.4：基本风速v0应按该规范 E.3 中规定的方法进行统计计算，重现期应取50年，v0取重现期为50年的最大风速。

E.3.1：对风速的统计样本均应采用年最大值 x，并采用极值Ⅰ型的概率分布，其分布函数为：

分布的参数与均值μ和标准差σ的关系按下述确定：

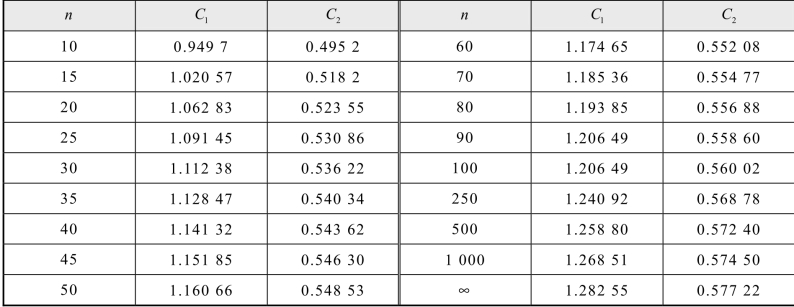
E.3.2：当由有限样本n的均值和标准差σ1作为μ和σ的近似估计时，取

系数C1、C2取值见表7.1-3。

表7.1-3　系数C1和C2取值

2.基本风压

（1）IEC 60826。

基本风压：

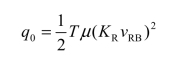
其中：q0为基本风压；T为空气密度修正系数；μ为空气密度，在海平面及气压101.3 kPa条件下等于 1.225 kg/m3；KR为粗糙度系数；vRB为B类地形的粗糙度系数。

（2）美国现行规范ASCE/SEI 7 Minimum Design Loads for Building and other Strucrures（《建筑物和其他结构的最小设计负荷》）中规定基本风速为离地 10 m 高，地面粗糙度为C，3s阵风风速，无飓风为地区重现期50年，飓风地区为重现期500年。其设计风压公式为：

式中：qz——速压（N/m2）；

　　　Kz——与高度和地形条件有关的地形影响系数；

　　　Kzt——与局部地形条件有关的影响系数；

　　　Kd——风向系数；

　　　v——根据空旷平坦地面上离地高度10 m处统计的50年一遇的3 s阵风风速。

（3）英国现行规范BS6399对于风压计算较为复杂，需考虑海拔、方向、季节、概率、地形。其计算公式为：

式中：qz为动态风压。

（4）《建筑结构荷载规范》（GB 50009—2012）。

基本风压：

其中：ρ——空气密度（t/m3）；

　　　v0——基本风速，基本风速重现期应取50年。

3.基本风速（压）选取

（1）《建筑结构荷载规范》（GB 50009）。

基本风压应按《建筑结构荷载规范》（GB 50009）规定的方法确定的50年重现期的风压取值，但不得小于 0.3 kN/m2。对于高层建筑、高耸结构以及对风荷载比较敏感的其他结构，基本风压的取值应适当提高，并应符合有关结构设计规范的规定。

全国各城市的基本风压值应按《建筑结构荷载规范》（GB 50009）附录E中表E.5重现期R为50年的值采用。当城市或建设地点的基本风压值在该规范表E.5中没有给出时，基本风压值应按该规范附录E规定的方法，根据基本风压的定义和当地年最大风速资料，通过统计分析确定，分析时应考虑样本数量的影响。当地没有风速资料时，根据附近地区规定的基本风压或长期资料，通过气象和地形条件的对比分析确定；也可以比照该规范附录E中附图E.6.3全国基本风压分布图近似确定。

（2）《轨道交通地面装置电力牵引架空接触网》（GB/T 32578）。

计算架空接触网设计用的基本风荷载时，应根据《建筑结构荷载规范》（GB 50009）规定，采用在规定重现期内、相对开阔的地形上、平均 10 min 期间内距离地面 10 m 处测量获得的环境风速作为基本风速。对于支持结构的设计，应采用《建筑结构荷载规范》（GB 50009）规定的50年一遇的最大风速。

（3）《高速铁路设计规范》（TB 10621—2014）。

运行基本风速应按正常行车风速确定，无确切资料时应按《铁路电力牵引供电设计规范》（TB 10009）确定。结构基本风速应根据《建筑结构荷载规范》（GB 50009），按50年一遇基本风压计算确定。

（4）《铁路电力牵引供电设计规范》（TB 10009—2016）。

接触网设计的气象条件，应根据最近记录年限不少于20年的沿线气象资料计算，并结合既有电气化铁路或高压架空送电线路的运行经验确定。

接触网的最大设计风速，应采用空旷地区、离地面 10 m 高处的 10 min 自动记录 15 年发生一次的平均最大值；接触网的结构设计风速，应采用空旷地区、离地面 10 m 高处的 10 min自动记录 50 年发生一次的平均最大值。如气象台（站）的记录值不满足上述要求，则应按规定进行换算。

4.风压高度变化系数

大气边界层内风速沿高度而增大，变化规律与地面粗糙度和温度垂直梯度及其他风气候有关。风速随着高度的增大逐渐变大，到达一定高度后高度再增加风速也不再增大，这个高度叫梯度风高度，一般为 300～500 m。我国相关规范认为在建筑结构关注的近地面范围，风速剖面基本符合指数律。

我国规范对于风压高度变化系数给出了不同离地面或海平面高度与之对应的地面粗糙度的类别，根据实际的设计情况进行选取。我国规范分为A、B、C、D四种类别。《建筑结构荷载规范》（GB 5009—2012）中将风压高度变化系数如下：

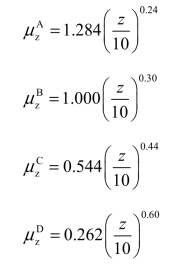
IEC规范与GB规范对于风压高度变化系数的规定是有区别的，首先对于地面粗糙度都分为A、B、C、D四类。GB规范对于地面粗糙度分类如下：

——A类指近海海面和海岛、海岸、湖岸及沙漠地区；

——B类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇和城市郊区；

——C类指有密集建筑群的城市市区；

——D类指有密集建筑群且房屋较高的城市市区。

IEC对于地面粗糙度分类如下：

——A类指广阔的水域或平坦的沿海地区；

——B类指只有少量障碍物的空旷野外，如机场或少量数目和建筑的耕地；

——C类指有很多低矮障碍物的地区，如围栏、树木、房屋；

——D类指近郊地区或有很多高大树木的地区。

表7.1-4、表7.1-5和图7.1-2所示为IEC规范以及国标规范对于风压高度变化系数的对比。

表7.1-4　风压高度变化系数计算公式对比

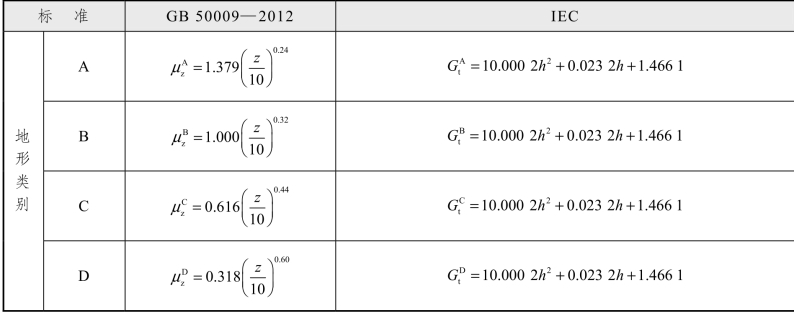
表7.1-5　风压高度变化系数对比

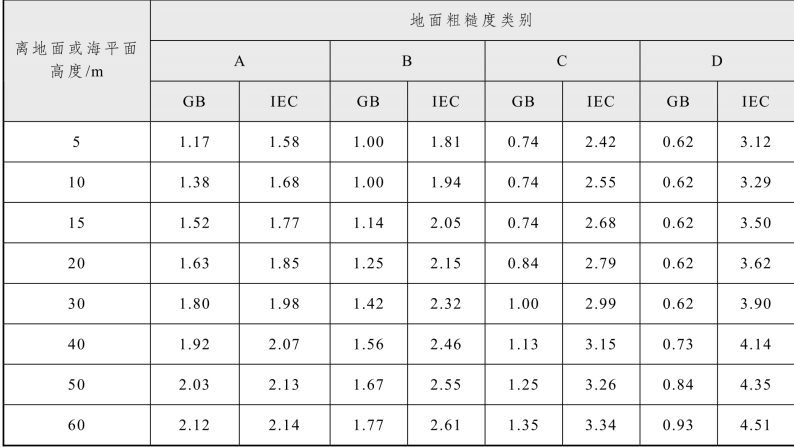
注：以上GB代表GB 500019—2012。

图7.1-2　GB规范与IEC规范风压高度变化系数对比(www.xing528.com)

从图表中可以看出，随着离地面或海平面高度的增加，在GB规范以及IEC规范中，风压高度变化系数都是从小增大的。这说明，两个规范对于风速沿高度变化的认知是一样的，即从低到高，风速是逐渐增大的，是呈现梯度分布的。但横向比较，地面粗糙度类别从A类到D类，GB规范中风压高度变化系数是逐渐减小的。说明GB规范认为，随着地面粗糙度类别的增加，风与地面的摩擦是增大的，相同高度下风速是要减小的。而IEC规范中地面粗糙度类别从A类到D类，风压高度变化系数是增大的。

美国规范对于风压高度变化系数采用的是风速压力暴露系数、风振系数和阵风影响系数。规范中也是规定不同离地面或海平面高度与之对应的地面粗糙度的类别，它们分为三类，与中国B、C、D相似，分别为：

（1）对于屋面平均高度小于等于 9.1 m 的建筑，暴露类别B适用于地面粗糙类为 B 类的地形应为在迎风方向大于 457 m；对于屋面平均高度大于等于 9.1 m的建筑，暴露类别B适用于地面粗糙类为B类的地形应为在迎风方向大于 792 m或建筑物高度的20倍以远处。

（2）暴露类别C用于暴露类别B或D不适用的所有情况。

（3）暴露类别 D 适用于地面粗糙类为 D 类的地形应为在迎风方向大于1 524 m或建筑物高度的20倍以远处，也适用于在迎风方向先经过之前定义的暴露类别 D 的地形，建筑物场地附近的地形粗糙度类别为 B 或 C，且该地形在 183 m 内或建筑物高度的 20 倍以内，取最大值。

5.风振系数

风振系数反映了结构在脉动风作用下的动力增大效应，一般通过随机振动方法或谱方法求解。对于工程结构，风荷载可采用以下两种方式：

方式一：风荷载＝平均风压＋等效风压，后者为脉动风引起的结构风振的等效效应。

方式二：风荷载＝平均风压×风振系数βz，通过风振系数来综合考虑结构在风荷载作用下的动力响应。

有关风振系数的相关规定主要有：

（1）《建筑结构荷载规范》（GB 50009）。

风振系数是为了综合考虑结构在风荷载作用下的动力响应，其中包括风速随时间、空间的变异性和结构的阻尼特性等因素。规范规定：对于高度大于 30 m且高宽比大于 1.5 的房屋，以及基本自振周期 T1大于0.25 s的各种高耸结构，应考虑风压脉动对结构产生顺风向风振的影响。采用风振系数法计算顺风向风荷载时，其取值应根据结构的自振周期、高度、基本风压等计算确定。目前常用的接触网钢柱采用 Midas Civil 2015 进行有限元建模分析，得出Gg220/10.5的自振周期为 0.5 s，GHT240/10.5 的自振周期为 0.6 s，格构式钢柱 G120/12 的自振周期为0.35 s，三种支柱的自振周期均大于 0.25 s，根据规范规定均需要考虑风振系数。当取基本风压为0.45 kN/m2时计算得到接触网支柱的风振系数约为1.6～2.2。

（2）《轨道交通 地面装置 电力牵引架空接触网》（GB/T 32578）考虑风振系数，其值取2.05。

（3）《铁路电力牵引供电设计规范》（TB 10009）不考虑风振系数，其值取1.0。

综上，《建筑结构荷载规范》（GB 50009）及《轨道交通 地面装置 电力牵引架空接触网》（GB/T 32578）均需考虑风振系数，两本规范计算得到的数值基本接近，其中《建筑结构荷载规范》（GB 50009—2012）的数值偏小。

6.体型系数

（1）规范及规定。

我国《架空输电线路杆塔结构设计技术规定》（DL/T 5154）中对角钢铁塔的阻力系数有明确规定。日本 JEC 规范中，根据角钢输电塔的风洞试验分别给出了不同结构类型阻力系数与挡风系数之间的关系。另根据我国《建筑荷载设计规范》GB 50009表8.3.1第35项，方形角钢塔架整体体型系数μs分别取2.6（0°）和2.9（45°）。

《建筑结构荷载规范》（GB 50009）中取格构式钢柱的体型系数为φ·1.3·（1+η），其中φ为挡风系数（φ=An/A，An为受风面有效面积，A 受风面投影面积），因此体型系数与计算面积的乘积为φ·1.3·（1+η）·A=1.3·（1+η）·An，η为根据桁架的挡风面积及宽高比计算确定的参数。

《轨道交通地面装置电力牵引架空接触网》（GB/T 32578）中格构式钢柱体型系数与计算面积的乘积为2.8An。

《铁路电力牵引供电设计规范》（TB 10009）中格构式钢柱的体型系数取值为 0.8 或φ·1.3·（1+η），具体取值以φ·1.3·（1+η）为准，即与《建筑结构荷载规范》（GB 50009）的取值相同。

（2）CFD数值分析。

接触网格构式桥钢柱属柔性体系，在正常运营阶段易发生多种类型风致振动响应，影响接触网的正常使用和结构安全，因此抗风性能是桥钢柱最重要的控制因素。目前，结构风工程的主要研究手段包括风洞试验、数值模拟和现场测试，其中风洞模型试验是主要研究手段。但随着钝体空气动力学理论和计算机硬件水平的进步，基于计算流体力学（CFD）技术的计算风工程（CWE）已取得令人瞩目的成绩，在桥梁气动选型、风振机理分析和抗风性能评估等研究中发挥着重要作用。

相对于物理风洞试验，数值模拟具有其诸多优点和良好的发展前景，费用低、效率高，便于进行抗风性能参数化分析，而且不受模型尺度影响，可较全面地考虑大气边界层风以及结构局部构造细节等的影响。

接触网支柱气动力数值计算：

① 计算方法。

使用计算流体力学程序 aFLOW 计算接触网角钢格构式钢柱的体型系数，该程序基于高性能的介观流体物理学方法——LatticeBoltzmann方程开发。

② 计算参数。

建立接触网格构桥钢柱的三维模型，并导入αFLOW前处理程序中，在直腿底部选取一个节段作为代表节段，如图7.1-3。

该节段高 1.8 m，顶宽 0.52 m，底宽 0.62 m，相应流向宽度为 0.42 m 和0.465 m。

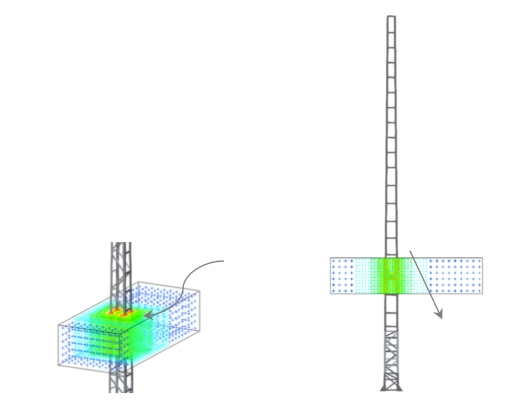
图7.1-3　角钢格构式钢柱体型系数的数值模拟模型

风偏角α=0°，顺线路方向。

流场离散最小尺寸：0.001 25 m，远场流场尺寸0.2 m。

边界条件：

入口：均匀流，流速40 m/s；

出口：压强边界，流场梯度为0；

上下左右：为固壁边界，模拟风洞边界墙体。

计算工况：

分别计算5个风偏角工况：0°、30°、45°、60°和90° 风偏角下非定常流场。通过对结构节段的表面进行流场压强积分，计算结构所承受的气动合力。

③ 数值计算结果。

a.0°风偏角工况。

图 7.1-4 是 0° 偏角下流场的速度剖面，可见杆件周围最大绕流流速为 69.6 m/s，且由于雷诺数约为1.7×105，故杆件尾流中旋涡尺度很小。

图7.1-5为该节段在0° 偏角下的体型系数的数值模拟结果，其时均值：

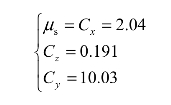
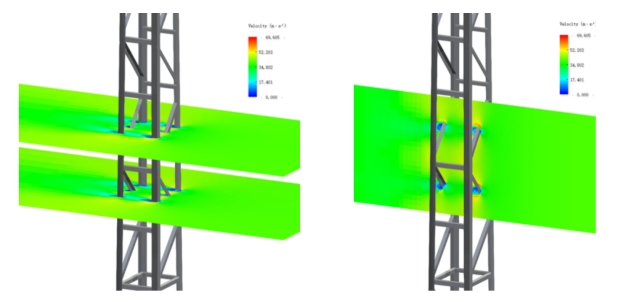
图7.1-4　流场速度剖面，风偏角α=0°顺线路方向

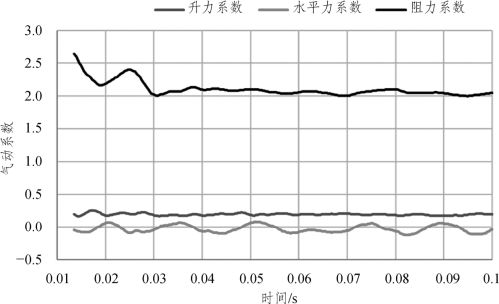
图7.1-5　角钢格构式钢柱节段体型系数，风偏角α=0°顺线路方向

b.30° 风偏角工况。

图7.1-6、图7.1-7和图7.1-8是30° 偏角下流场的速度剖面和涡量分布，可见杆件周围最大绕流流速为 73.3 m/s，且由于雷诺数约为 1.7×105，故杆件尾流中旋涡尺度很小。

图7.1-6　30° 风偏角流场速度剖面

图7.1-7　30° 风偏角支柱周围流场涡量分布

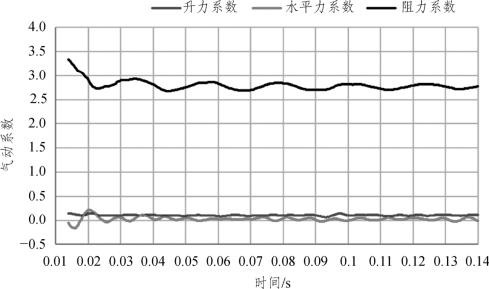
图7.1-8　30° 风偏角气动力数值计算时程

c.45° 风偏角工况。

图7.1-9是45° 偏角下流场的速度剖面，此工况阻风面积最大，可见杆件周围最大绕流流速为 73.3 m/s，且由于雷诺数约为 1.7×105，故杆件尾流中旋涡尺度很小。

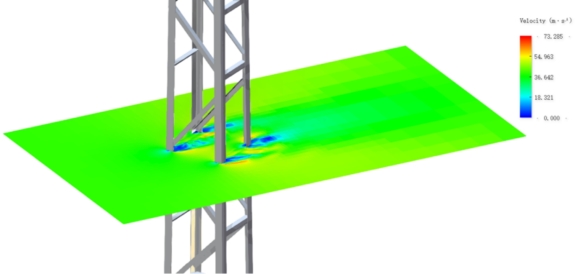
图7.1-9　45° 风偏角流场速度剖面

从气动力时程可见，因为采样时间较短，时程曲线中可见有规律的涡脱波动（图7.1-10）。

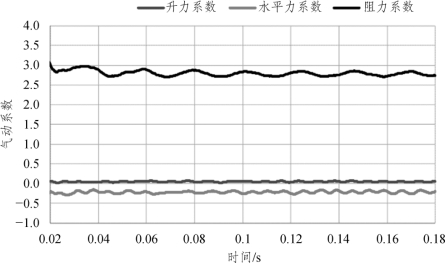
图7.1-10　45° 风偏角气动力数值计算时程

d.60° 风偏角工况。

图 7.1-11 是60° 偏角下流场的速度剖面和涡量分布，可见杆件周围最大绕流流速为68.7 m/s，且由于雷诺数约为1.7×105，故杆件尾流中旋涡尺度很小。

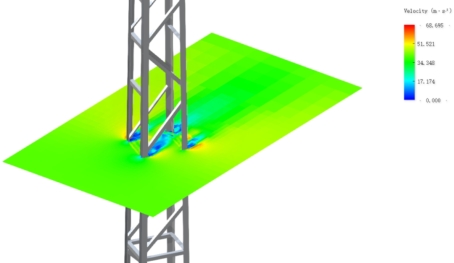
图7.1-11　60° 风偏角流场速度剖面

从气动力时程可见，因为采样时间较短，时程曲线中可见有规律的涡脱波动（图7.1-12）。

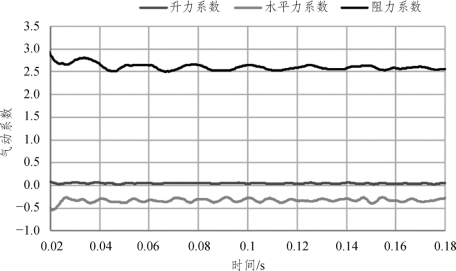
图7.1-12　60° 风偏角气动力数值计算时程

e.90° 风偏角工况。

图 7.1-13 是 90° 偏角下流场的速度剖面，可见杆件周围最大绕流流速为71.6 m/s，且由于雷诺数约为 1.7×105，故下游杆件处在上游杆件的尾流中，未见大尺度涡脱。

图7.1-13　90° 风偏角流场速度剖面

从气动力时程可见，由于杆件尺寸小，因此时程曲线包含了丰富的高频小尺度涡脱（图7.1-14）。

图7.1-14　90° 风偏角气动力数值计算时程

④ 气动力汇总。

不同风偏角气动力系数如表7.1-6。

表7.1-6　不同风偏角桥钢柱体型系数

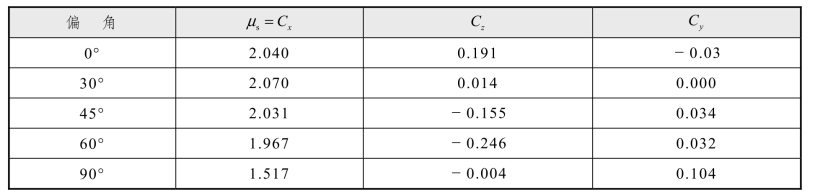
从表中可看出，数值模拟水平和竖向气动力的数值均较小，且波动较大。根据《建筑结构荷载规范》（GB 50009—2012）表8.3.1第35项：角钢塔架体型系数为2.27，略大于数值计算结果，因此采用规范给出的体型系数偏保守，在设计时可按照规范进行选取。

7.结论

（1）海南环岛铁路接触网结构在强台风环境下可采用《建筑结构荷载规范》（GB 50009）中的计算方法，其中基本风压应根据海南环岛沿线气象台站重现期最大风速或《建筑结构荷载规范》（GB 50009）中 50 年重现期基本风压综合确定，并相应对海拔、地形、高度、温度、体型等进行修正；同时还应进行历史记录的最大台风风速下强度破坏校核。

（2）海南环岛铁路接触网结构在强台风环境下风荷载计算应考虑风振系数，在设计时可选用《轨道交通地面装置电力牵引架空接触网》（GB/T 32578）中规定的2.05进行计算。