1.桥上无缝道岔分析理论与方法
(1)道岔-桥梁相互作用原理。
桥上铺设无缝道岔后,道岔与桥梁之间的相互作用与桥上无缝线路的梁轨相互作用既有共性又存在差异。道岔与桥梁之间的相互作用更加复杂,梁体随温度变化的伸缩、在竖向荷载作用下的挠曲、列车的制动/加速会引起桥梁与道岔的相互作用,另外,道岔里轨由于温度变化引起的伸缩不仅造成里轨与基本轨的相互作用,而且通过扣件、桥面系引起道岔与桥梁的相互作用,道岔-桥梁相互作用是这两种作用相互耦合与相互叠加后的综合效果。道岔-桥梁相互作用原理可以定义如下:在梁体温度变化、列车荷载、列车制动/加速以及道岔里轨随温度变化伸缩的作用下,梁和桥上轨道(包括道岔)之间产生相对位移,桥上轨道(包括道岔)产生钢轨纵向附加力,对桥面系作用大小相等、方向相反的反作用力,此力通过梁、支座传递至墩台,在桥上轨道(包括道岔)与桥梁之间形成一个相互作用的力学平衡体系。道岔-桥梁相互作用原理是桥上无缝道岔纵向力和位移计算的理论基础。道岔与桥梁之间的相互作用如图5.2-8所示。
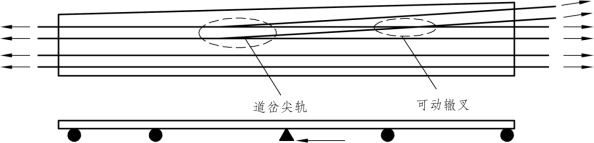
图5.2-8 道岔与桥梁之间的相互作用
道岔与桥梁之间相互作用力包括伸缩力、挠曲力、断轨力和制动力。
(2)道岔-桥梁相互作用非线性有限元模型计算假定:
① 道岔尖轨与可动心轨前端可自由伸缩。尖轨或可动心轨尖端位移为其跟端位移与自由段伸缩位移之和。
② 不考虑辙叉角大小的影响,假设导轨与长轨条平行。
③ 钢轨按支承节点划分有限杆单元,只发生纵向位移;岔枕按钢轨支承点划分有限杆单元,可发生纵向位移和转角。
④ 扣件纵向阻力模拟为纵向弹簧,作用于钢轨节点和岔枕节点上,方向为阻止钢轨相对岔枕位移。扣件阻力可分别按常量和变量输入。
⑤ 不考虑钢轨与岔枕间的相对扭转。桥上无缝道岔若设置有伸缩调节器,假定其纵向约束阻力为零;若设置有普通接头,假设接头阻力为定值;若考虑伸缩调节器的纵向阻力时,视其为普通接头。
⑥ 道床阻力以单位岔枕长度的阻力计,道床阻力沿岔枕长度方向均匀分布。道床阻力可分别按常量和变量输入。
⑦ 考虑间隔铁阻力对钢轨伸缩位移的影响。间隔铁阻力以弹簧单元模拟,可分别按常量和变量输入。岔枕与桥梁、钢轨与路基间的纵向约束阻力均假定为纵向弹簧约束。
⑧ 考虑辙跟限位器在基本轨与导轨间所传递的作用力,设道岔铺设时限位器子母块位置居中,间隔为 7 mm。当子母块贴靠时,限位器子母块接触刚度按常量和变量输入。桥梁墩台顶纵向刚度假定为线性,包含在支座顶面纵向水平力作用下的墩身弯曲、基础倾斜、基础平移及橡胶支座剪切变形等引起的支座顶面位移。桥梁墩台及基础的竖向刚度即为桥梁支座竖向刚度。
⑨ 假设桥梁固定支座能完全阻止梁的伸缩,活动支座抵抗伸缩的阻力可略而不计,暂不考虑支座本身的纵向变形,固定支座承受的纵向力全部传递至墩台上。梁在支座外的悬出部分,计算伸缩量时不考虑。其他支座形式,需根据其受力特点另外进行数学简化。有砟桥上假设道床所承受的纵向阻力全部传递至桥梁墩台上。
⑩ 在计算伸缩力时,梁的温度变化仅为单纯的升温或降温,不考虑梁温升降的交替变化,一般取一天之内的最大梁温差计算梁的伸缩量。桥上无缝道岔的伸缩力、挠曲力、断轨力均以最大轨温变化幅度作为计算条件;对挠曲力、伸缩力、断轨力、制动力分别计算,不考虑叠加影响。
(3)岔梁墩一体化计算模型。
岔梁墩一体化计算模型如图5.2-9~图5.2-11所示。
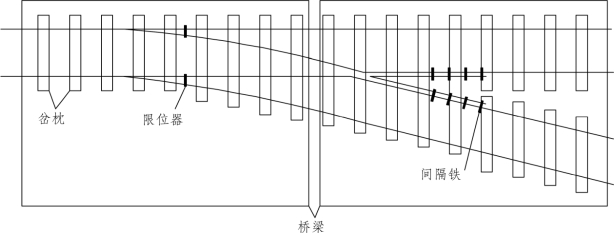
图5.2-9 桥上无缝道岔模型平面图
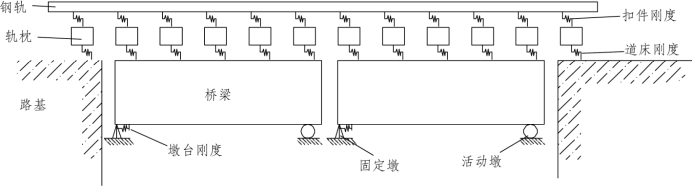
图5.2-10 有砟桥上无缝道岔模型立面图
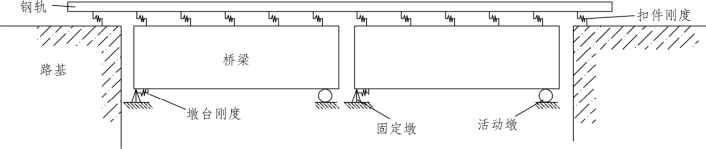
图5.2-11 无砟桥上无缝道岔模型立面图
在有砟桥上无缝道岔计算模型中,道岔里轨发生伸缩位移后,带动岔枕纵向移动和偏转,一部分作用力通过扣件传递给基本轨,一部分作用力通过岔枕传给道床再传递给桥梁。桥梁因伸缩或挠曲在梁面上产生纵向位移,墩台因道岔上传下来的力在墩顶产生纵向位移,并带动桥梁产生纵向位移。同时,梁的位移通过道床传到道岔上,会导致钢轨中的纵向力重新分布,进而再影响桥梁的受力与变形。
在无砟桥上无缝道岔计算模型中,道岔里轨发生伸缩位移后,通过无砟轨道传递作用力到桥梁上,限位器子母块接触后,一部分作用力通过限位器传递给基本轨,一部分作用力通过无砟轨道再传递给桥梁。桥梁因伸缩或挠曲在梁面上产生纵向位移,墩台因道岔上传下来的力在墩顶产生纵向位移,并带动桥梁产生纵向位移。同时,梁的位移通过无砟轨道传到道岔上,会导致钢轨中的纵向力重新分布,进而再影响桥梁的受力与变形。
(4)程序编制。
通用有限元软件在非线性分析方面技术已非常成熟,计算功能也强大,计算效率和可靠度很高。本节利用通用有限元软件开放的体系结构,基于通用有限元软件二次开发技术编制了梁轨相互作用非线性有限元程序DCWTB,它采用命令流技术来控制程序流程,自动完成有限元建模、荷载的施加、方程的求解,极大地提高了计算精度和工作效率。图5.2-12为通用有限元中建立的桥上无缝道岔有限元模型(一组单渡线)。
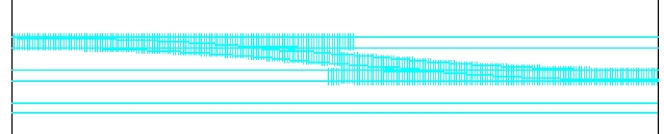
图5.2-12 桥上无缝道岔有限元模型
2.桥上12号无砟无缝交叉渡线纵向受力研究
(1)桥上岔区无砟轨道系统的组成:
① 凸台式结构:台式无砟道岔结构主要以Rheda无砟轨道为代表,采用轨枕埋入式结构,轨枕配置外露的桁架筋加强与现浇混凝土道床的联结。预制混凝土枕现场浇筑于道床板内,并通过纵向钢筋和双块式轨枕的桁架筋确保轨枕与道板的可靠联结。现浇道床板较好地保证了结构的整体性,不需要设置专门的调整层,随着道床的施工完成,轨道空间几何状态也就调整就位。桥上岔区Rheda轨道结构如图5.2-13所示,由道岔、混凝土桁架岔枕、混凝土道床板、隔离层、凸台、保护层等组成。

图5.2-13 无砟桥上岔区轨道结构
② 道岔板:桥上无缝道岔的道岔板被分块浇筑,分块长度是根据道岔要求确定的。道床板之间的接缝还可以用作桥面的排水。轨道板的宽度随着道岔的几何尺寸而有所不同。轨道板的高度由于桥梁横向坡度的不同而有变化,并取决于轨道板的宽度。道岔板典型的构造如图5.2-14所示。
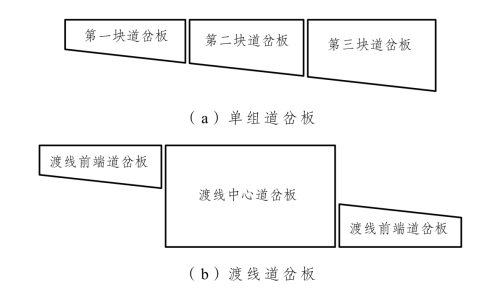
图5.2-14 道岔板布置示意
③ 凸台:沿着轨道板长度方向保护层上有一个纵向的凸台,而沿着轨道板整个宽度方向上大约有三个横向的凸台固定道岔板。纵横向水平力通过一个纵向的和三个或四个横向凸台从道岔板上传递到保护层。纵向凸台采用钢筋混凝土结构,高 60 mm,宽800 mm,间距为13 000 mm;横向凸台采用钢筋混凝土结构,高 60 mm,宽 500 mm,横向凸台的长度则取决于道岔的几何尺寸。凸台的边缘有角钢保护,这些预制的角钢焊接在锚杆和连接筋上。凸台采用箍筋进行加固,道岔板的凸台边缘也采用角钢进行保护。
④ 隔离层:混凝土保护层的水平面和凸台上覆盖着连续隔离层。隔离层旨在把无砟轨道混凝土和保护层混凝土分离开。隔离层由一层厚 1.3 mm 的EPDM橡胶垫片和一层 0.4 mm厚的 PE 垫片组合而成,这种垫片允许由于无砟轨道结构的温度梯度变化等引起的各种伸缩和滑动。为确保转移荷载的安全性,在凸台的垂直面上要安装弹性支座。支座材料为CalenbergS70 型弹性支座,按不同的弹性要求,分为D、E、F等三个规格。有3个横向凹台和4个横向凸台的两种情况,如图5.2-15所示。
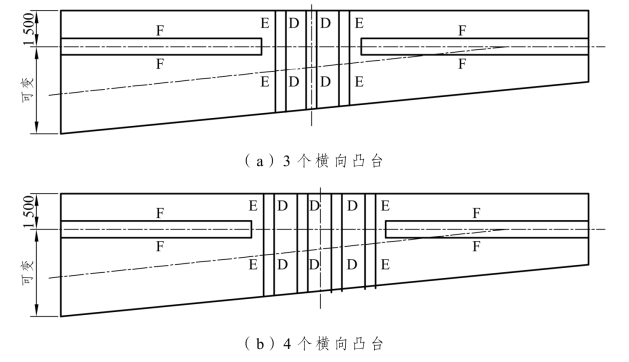
图5.2-15 横向凸台的弹性支座分布示意图(单位:mm)
⑤ 保护层:保护层是在梁上连续浇筑、覆盖整个梁面的混凝土轨道板,只有在梁缝处保护层才是断开的。荷载通过防护层与桥面板之间的摩擦以及保护层与脱轨防撞墙之间的连接钢筋传递到梁上。
⑥ 门型钢筋结构:地铁工程中,桥上岔区无砟轨道经常采用钢筋混凝土短岔枕埋入式结构。根据铺设位置不同,短岔枕可分为不同长度,但应尽量减少类型,短岔枕内预埋塑料套管,用螺栓将垫板与短岔枕连接,短岔枕底部伸出钢筋与整体道床相连接。整体道床伸缩缝应尽量避开转辙器、辙叉和护轨部分。道岔整体道床范围应尽量避开结构沉降缝。桥上道岔道床应做好排水处理,并与桥梁本身排水设施相匹配,道床表面适当设排水横坡。通过在桥梁保护层中预埋门型钢筋的形式将道床板和桥梁进行连接,门型钢筋采用φ 16HRB335钢筋,沿线路纵向每隔 650 mm 布置一排,尖轨、里轨和辙叉所在道床每排根数不相同。在门型钢筋两侧设置分布定位钢筋。道床板断面如图5.2-16所示。
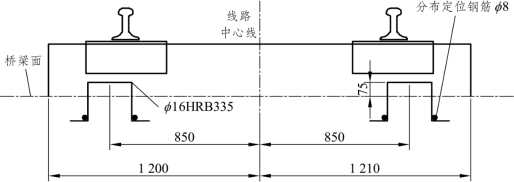
图5.2-16 地铁道岔区道床板断面图(单位:mm)
(2)计算模型及参数。
桥上无缝道岔和路基无缝道岔的区别主要在基础上:路基上无缝道岔两边都位于固定区,只有道床阻力在纵向上对其产生影响;而桥上无缝道岔存在基础的纵向变形,即使钢轨没有温度变化而桥梁有温度变化也存在温度附加力和位移。但是桥上无缝道岔基础竖向位移比较小,主要包括墩台的沉降和桥梁的挠曲;而路基上无缝道岔基础不发生比较大的沉降,而且沿线路方向沉降差异很大。
为了研究无砟轨道桥上无缝道岔交叉渡线受力和变形情况,课题组从整个线桥系统出发,基于非线性有限单元法建立了“轨-枕-板-桥-墩”空间一体化纵向力计算模型,考虑了线路纵向阻力、桥梁纵向水平刚度以及轨道和桥梁本身变形,如图5.2-17所示。

图5.2-17 有限元计算模型
① 钢轨:交叉渡线(混凝土岔枕、60 kg/m钢轨、92改进型12号可动心轨辙叉、5 m间距)的平面示意图及有关说明如图5.2-18所示。
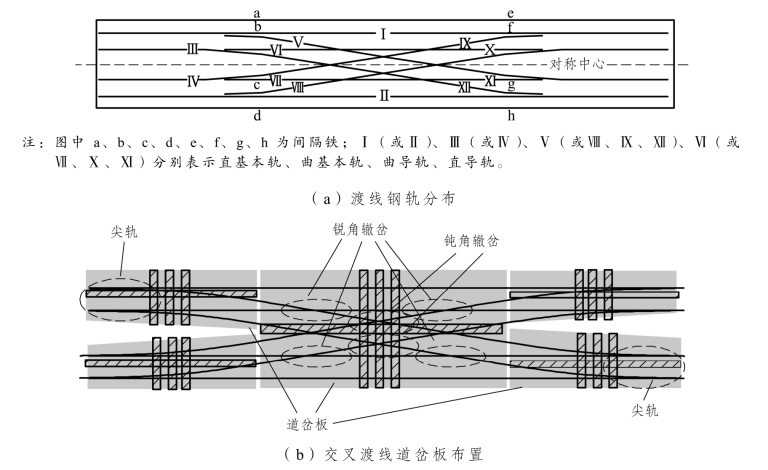
图5.2-18 交叉渡线平面示意
混凝土岔枕、60 kg/m钢轨、92改进型12号可动心轨辙叉、5 m间距交叉渡线,道岔总长155个枕跨,导曲线半径350.717 m,岔枕间距为0.6 m。道岔直侧股均焊接。
② 轨枕:轨枕采用梁单元模拟,截面积 A=61 600 mm2,竖直轴的惯性矩Izz=4.05×108 mm4,横轴的惯性矩 Ixx=2.48×108 mm4,混凝土岔枕弹性模量E=3.25×107 N/mm2,泊松比0.2。
③ 区间扣件阻力:扣件纵向阻力由钢轨与垫板之间的摩阻力和扣板与轨底扣着面之间的摩阻力组成,摩擦阻力大小取决于扣压力和摩擦系数的大小。当扣件螺母扭矩一定时,扣件纵向阻力随着钢轨纵向位移增加而增大,当位移达到某一程度之后,钢轨开始滑移,其阻力不再增加。在相同的位移下,扣件螺母扭矩越大,扣件纵向阻力越大。北京交通大学对我国Ⅰ、Ⅱ、Ⅲ型扣件的扣件纵向阻力进行了测试,得出了扣件纵向阻力与位移关系曲线。由测试结果可知,对于小于 1 mm 的位移,有弹性位移的性质,而 1 mm 之后,钢轨开始有滑移趋势。北京交通大学建议,Ⅰ、Ⅱ、Ⅲ型扣件的阻力可采用表5.2-2的取值。
表5.2-2 扣件纵向阻力

④ 岔区扣件阻力:扣件为Ⅲ型,扭矩为 70~90 N·m 时,其纵向阻力是非线性的,故模拟扣件时采用非线性弹簧单元模拟。由室内试验得出扣件阻力和位移的关系,确定非线性弹簧的参数,Ⅲ型扣件纵向阻力测试值见表 5.2-3,计算中扣件阻力若取为常值,则取为16 kN。
表5.2-3 扣件阻力

⑤ 桥上小阻力扣件:借鉴桥上无缝线路的经验,桥上部分采用小阻力扣件,桥上小阻力单轨扣件极限阻力值为66.7 kN/cm,其拟合公式为:
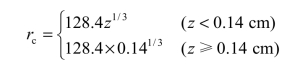
对于小阻力扣件,在混凝土桥梁无砟轨道线路伸缩力计算中,中国“暂规”规定纵向阻力取值以小阻力为准。对无载工况,线路纵向阻力取值为小阻力扣件极限纵向阻力的 0.75倍;对有载工况,机车、车辆下纵向阻力分别取小阻力扣件极限纵向力的1倍和0.75倍。
⑥ 限位器、间隔铁阻力:限位器子母块在不同荷载条件下的测试位移如表5.2-4所示。
表5.2-4 限位器子母块位移

间隔铁阻力计算中采用常量阻力时,可取为5×104 kN/m。
⑦ 凸台及弹性支座参数:凸台与轨道板之间的约束关系用弹簧单元模拟。参考《RHEDA2000无砟轨道技术转让》的相关内容,推导出支座的刚度。分析得出:10 mm厚D胶垫和15 mm厚E胶垫刚度在250~300 kN/mm成线性变化;5 mm厚 F 胶垫在 1.74 mm 以内成线性变化,刚度值为 270~300 kN/mm,超出1.74mm以后成非线性变化,刚度值为350 kN/mm~无穷大。如图5.2-19所示。
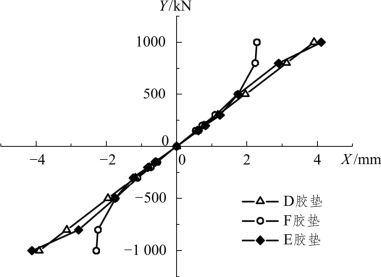
图5.2-19 凸台胶垫支座刚度变化曲线
⑧ 门型筋:根据国内城市轨道交通桥上道岔建设经验,为了在相同条件下比较两种不同的基础连接形式,在本计算模型中,门型钢筋用线性弹簧单元进行模拟,刚度取为无穷大,如图5.2-20所示。

图5.2-20 道岔板门型钢筋布置
通过在桥梁保护层中预埋门型钢筋的形式将道床板和桥梁进行连接,门型钢筋沿线路纵向布置,纵向间距 600 mm,第一块渡线板、第二块渡线板每排设置两组,渡线中心板每排设置五组,在门型钢筋两边设置定位钢筋。
⑨ 轨道板:轨道板采用实体单元模拟,轨道板高 0.37 m,渡线中心板宽7.8 m,渡线板宽有2.8~3.5 m,材料参数按C40混凝土取值。
⑩ 保护层和桥梁板:保护层和桥梁板为一体,采用实体单元模拟,保护层和桥梁板高度为0.5 m,宽为13.2 m,其余参数取与轨道板参数相同。
(3)岔桥位置及相关参数。
交叉渡线平面如图5.2-21所示,铺设在一座(32+48+32)m的混凝土连续梁上,两边为32 m简支梁,桥梁两边各考虑了 65 m 的路基影响范围,道岔菱形对称中心布置在连续梁中间部位,其桥跨长度及支座布置如图5.2-22所示。渡线辙跟设两个限位器,间隙值为 7 mm。道岔总长 155 个枕跨,导曲线半径350.717 m,岔枕间距为 0.6 m。道岔直侧股均焊接。以菱形对称中轴位置表示坐标零点,钢轨及桥墩位移向右为正,向左为负。
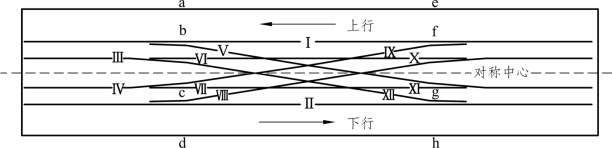
图5.2-21 交叉渡线平面示意
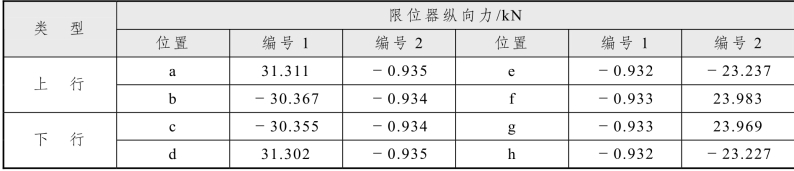
注:图中a、b、c、d、e、f、g、h为间隔铁或限位器,同时也代表尖轨编号;Ⅰ(或Ⅱ)、Ⅲ(或Ⅳ)、Ⅴ(或Ⅷ、Ⅸ、Ⅻ)、Ⅵ(或Ⅶ、Ⅹ、Ⅺ)分别表示直基本轨、曲基本轨、曲导轨、直导轨。

图5.2-22 桥跨及支座布置(单位:m)
连续梁固定支座纵向刚度 200 kN/mm,简支梁固定支座纵向刚度100 kN/mm,左右桥台纵向刚度300 kN/mm。
3.桥上12号无砟无缝交叉渡线温度力分析
设钢轨升降温幅度 50 °C、轨道板升降温幅度 30 °C、桥梁升降温幅度 15 °C,进行岔、桥温度力作用分析。计算、分析结果如下:
(1)直基本轨纵向附加力和纵向位移。
图5.2-23所示为无砟桥上无缝交叉渡线在伸缩力作用下,直基本轨附加纵向力。直基本轨最大附加温度拉力为 485 kN,出现在:在①菱形对称中轴处,远离对称中轴;在②连续梁上道岔板伸缩缝处附加伸缩力减小;在③一方面是由于限位器处附加伸缩力增大,曲基本轨通过传力部件(限位器),把纵向力传递给了直基本轨,导致在辙跟处附加伸缩力增大,另一方面是由于钢轨和道岔板升降幅度不一致,在道岔板中部受拉;在④连续梁上道岔板与小板的伸缩缝处出现附加温度拉力;在⑤连续梁与简支梁梁缝处出现最大附加温度压力;在⑥简支梁与简支梁梁缝处又出现附加温度压力峰值;在⑦简支梁与路基接壤的墩台处,又再次出现附加温度压力峰值。在简支梁上的单元板,在单元板的伸缩缝处出现小的附加伸缩力。道岔两边以菱形对称中轴对称,左边的变化趋势与右边相同。但左右的峰值却有差异,因为连续梁固定支座布置在菱形对称中轴的右侧,可见固定支座的布置方式对桥上道岔直基本轨的受力影响明显。
直基本轨的伸缩位移见图 5.2-24。直基本轨最大纵向位移 8.12 mm,发生在尖轨尖端后不远处,这是因为:桥梁在伸缩力作用下发生变形,带动轨道板整体移动,轨道板在扣件的作用下带动钢轨伸缩,钢轨因为桥梁的伸缩和其自身在伸缩力作用下伸缩,两种方式其位移的不同主要是由于轨道板和桥梁降温幅度不一致,凸台形式因为降温幅度不同而使轨道板和桥梁之间有相对位移。
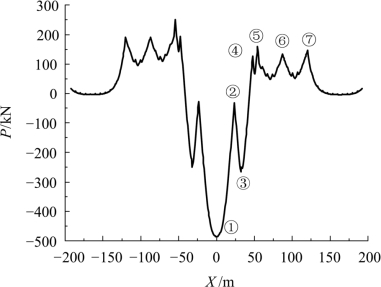
图5.2-23 直基本轨附加伸缩力
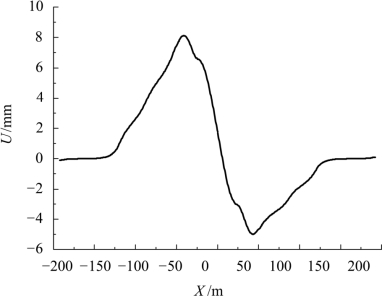
图5.2-24 直基本轨纵向位移
(2)道岔传力部件纵向力。
道岔传力部件的受力见表5.2-5所示。
计算表明,当设置两个限位器时,只有两边的限位器跟基本轨发生相互作用关系,内侧的限位器钢轨还没有贴靠(设置当纵向力为1kN时发生贴靠)。
表5.2-5 传力部件受力
(3)道岔尖轨位移。
在伸缩力作用下,尖轨绝对位移和板轨相对位移见表 5.2-6 所示,从中可以看出,道岔尖轨板轨相对位移均未超出转辙机的允许范围 15 mm,转辙机可以正常运转。
表5.2-6 尖轨位移

(4)凸台纵向力。
桥梁板与轨道板之间的约束关系是通过凸台来实现的,凸台上的弹性支座可以缓冲单一形式凸台上的荷载,有利于在收缩和温度荷载情况下凸台的受力。其凸台和弹性支座共同作用下的受力情况见图5.2-25所示。
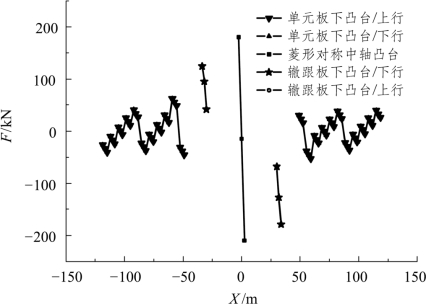
图5.2-25 凸台纵向力
由图可知,简支梁上的 5 块单元板下凸台纵向力的变化范围为-52.69~62.808 kN,其中在左边连续梁与简支梁连接处,出现简支梁上凸台的最大值,单个简支梁上的5块单元板,以中间单元板为对称中心,两边一边承受压力,一边承受拉力;菱形对称中心板下的凸台的纵向力变化范围为 180.01~-209.81 kN,以中间凸台为中心,一侧承受压力,一侧承受拉力;辙跟下的凸台纵向力的变化范围,左边为-41.1~124.45 kN,单边受拉,右边为-68.13~-178.94 kN,单边受压。可见在右边辙跟下凸台承受的纵向力要比左边的大,原因是连续梁固定支座布置的影响,固定支座限制了连续梁的位移,进而通过凸台限制了轨道板和钢轨的位移,所以在此处凸台与轨道板作用力大。
(5)桥墩纵向力。
桥梁固定支座所在墩台纵向力见表 5.2-7。由表可知,连续梁固定支座的纵向力最大,其值为365 kN。与连续梁相邻的简支梁固定支座纵向力也较大,尤其是连续梁温度跨度较大一侧的3号墩,纵向力达到242 kN。
表5.2-7 桥墩纵向力

(6)轨道板应力和位移。
① 轨道板应力。
道岔板和单元板的等效应力云图如图5.2-26 所示。由应力云图可以得知:桥上道岔板和单元板第一主应力的主要变化范围为-1.15~1.539 MPa,在菱形对称中心和菱形道岔板的中间部分出现部件6.916 MPa的应力,是因为该处轨枕的影响,在该处岔枕是断开的;桥上道岔板和单元板的等效应力的变化范围为1.162~9.226 MPa,其中板上表面的应力变化比较均匀,因为轨枕和混凝土共同作用,而板下的应力变化在凸台的地方应力较没有凸台的地方大,可见凸台对轨道板的受力影响是很明显的。由于整个模型成对称分布,右半部分应力分布同上所述。

图5.2-26 道岔板和单元板上表面等效应力云图
② 轨道板纵向位移。
道岔板和单元板的位移云图如图5.2-27所示。由位移云图可以得知,道岔板和单元板的纵向位移的变化范围为-12.403~8.86 mm。在连续梁上,辙跟下道岔板的左端和右端出现最大纵向负位移和最大纵向正位移,因为此处的道岔板和桥梁板的长度最长,受连续梁上固定支座的影响,使左端较右端的伸缩位移大;在简支梁上,在简支梁的两端单元板的纵向位移较简支梁中间部位的道岔板位移大,因为在温度力作用下,简支梁由中间向两边伸缩,通过凸台带动轨道板发生伸缩位移,在两端形成较中间大的纵向伸缩位移。可见相对升降温幅度对道岔板的伸缩位移影响是十分明显的。

图5.2-27 道岔板和单元板左边纵向位移云图
4.轨道结构参数影响分析
无缝道岔交叉渡线部件众多,其受力和变形比较复杂,而桥上铺设无缝道岔,桥梁的伸缩对道岔产生作用,而道岔的温度力又反作用于桥梁,这样,无缝道岔的受力和变形就变得更加复杂。弄清各种因素对桥上无缝道岔的影响,是桥上无缝道岔的设计、施工以及养护维修的核心内容。根据理论分析,轨道结构中对桥上无砟轨道无缝道岔受力与变形的影响因素有很多,下面就以下几种关键参数的影响进行分析:轨温变化幅度、扣件阻力、凸台刚度和岔区轨道板分块布置影响。
(1)轨温变化幅度的影响分析。
① 直基本轨附加温度力和位移。
直基本轨附加温度力和位移的变化如图5.2-28、图5.2-29所示。
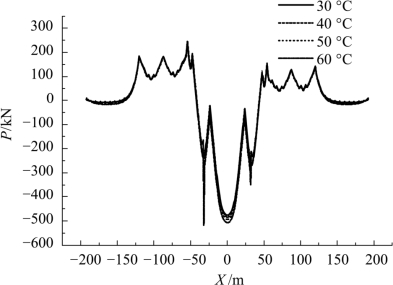
图5.2-28 直基本轨附加纵向力
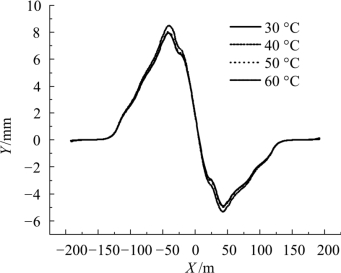
图5.2-29 直基本轨位移
上图表明:随着轨温变化幅度的增加,基本轨附加温度拉力和位移都逐渐增加,但增幅不大。
② 凸台纵向力。
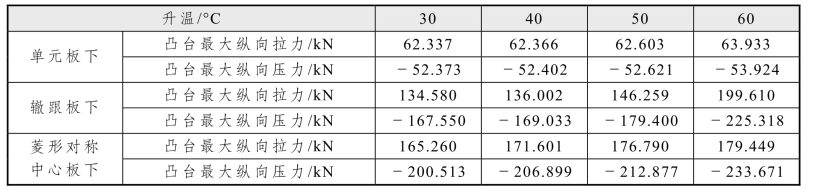
表 5.2-8 所列为凸台所受纵向力,随着轨温变化幅度的增加,单元板下凸台纵向力增加不是很明显,原因是单元板的长度比较短,轨道板和桥梁板之间通过凸台传递纵向力,凸台上的弹性胶垫能够有效地释放部分纵向力,减小轨道板和梁之间的作用力。辙跟板下凸台受力增加幅度比较明显,因为辙跟板处在梁伸缩位移和钢轨伸缩位移比较大的部位,轨道板和梁的相对位移大,纵向作用力增加幅度就大。菱形对称中心板下,凸台的纵向作用力增幅不大,原因是菱形对称中心部位是轨道板和桥梁板伸缩位移最小的地方,相对位移较小,作用力增幅不大。
表5.2-8 凸台纵向力
③ 其他。
计算同时表明,当升温 46 °C时,限位器子母块发生贴靠,随着轨温幅度的增加,限位器作用力增幅比较明显,导致基本轨纵向力增加幅度比较大,见表5.2-9。
表5.2-9 不同升温幅度下有关部件计算结果
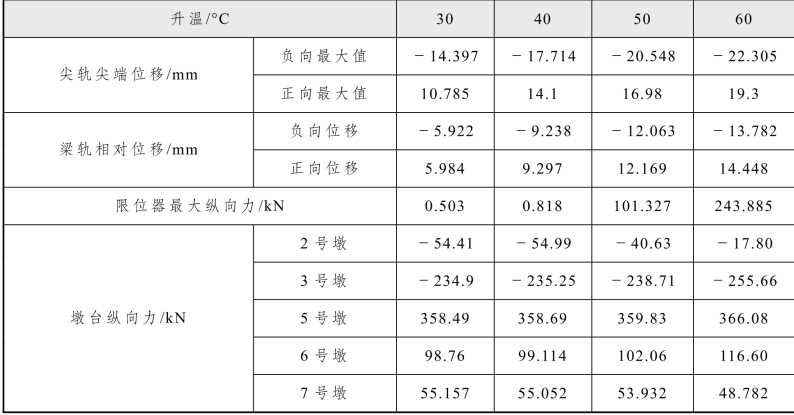
随着轨温幅度的增加,尖轨尖端的位移不断增大,梁轨的温差为45℃时,梁轨相对位移仍然没有超出 15 mm 转辙器要求的检算范围,可见转辙器放在桥上可以正常运转。
随着轨温变化幅度的增加,连续梁固定支座纵向力变化不大,对简支梁固定支座纵向力影响也不大。
从以上分析可知:轨温变化幅度的增加,对直基本轨附加温度拉力、道岔传力部件纵向力、道岔尖轨位移、梁轨相对位移和辙跟板下凸台纵向力影响明显,而对直基本轨附加温度压力、单元板下凸台纵向力、菱形对称中轴板下凸台纵向力和桥墩纵向力影响不大。可见,在轨道板和桥梁温差保持不变的条件下,随着轨温变化幅度的增加,虽然梁、轨温差不断增加,但梁轨相互影响并不大,所以对直基本股附加温度压力的影响也不大。由此可见,由于交叉渡线和梁跨均为对称布置,仅固定支座偏离对称中心,因此,在只有钢轨温度变化的条件下,桥梁和轨道结构受影响不大,钢轨和传力部件受影响较大。
(2)扣件阻力影响。
扣件是梁轨之间作用的重要传力部件,其阻力值对轨道结构的受力和位移影响很大,下面就改变扣件阻力参数进行比较分析。
荷载工况:钢轨升降温幅度 50 °C、轨道板升降温幅度 30 °C、桥梁升降温幅度15 °C。
① 简支梁桥上扣件阻力影响。(https://www.xing528.com)
改变简支梁上轨道扣件阻力,选取三种扣件作研究:弹条Ⅰ型扣件,滑移阻力为 5 kN/mm;弹条Ⅱ型扣件,滑移阻力为 16.1 kN/mm;弹条Ⅲ型扣件,滑移阻力为 23 kN/mm。岔区仍然采用非线性扣件阻力,对轨道结构进行对比分析,计算结果见表5.2-10。
表5.2-10 简支梁扣件阻力变化的计算结果
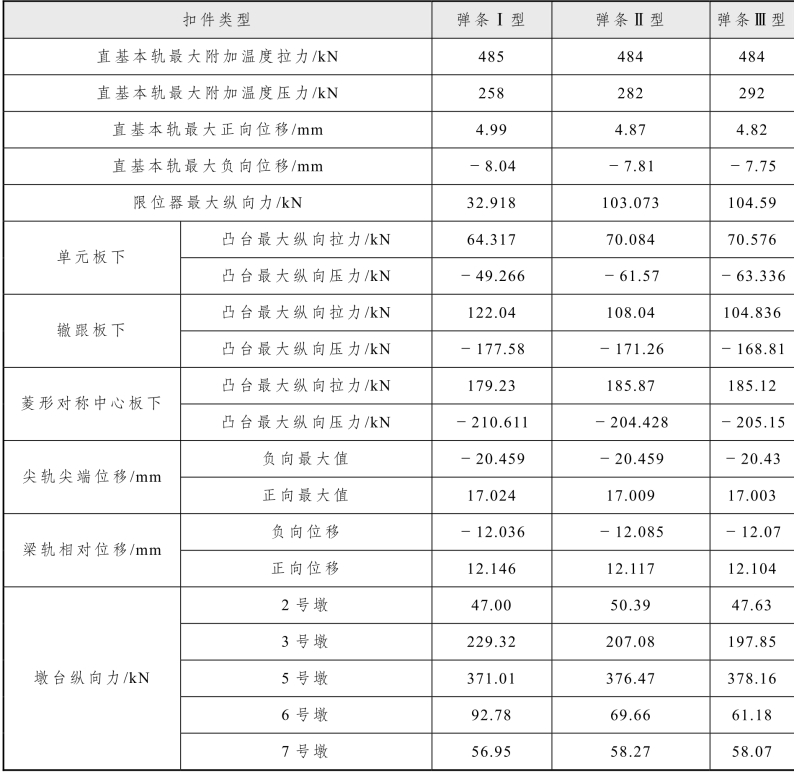
由计算结果可知:随着简支梁上轨道扣件阻力增加,连续梁上钢轨纵向力和钢轨位移变化不大,简支梁上在单元板伸缩缝处钢轨纵向力增加明显,钢轨纵向位移变化不大。直基本轨最大附加温度拉力变化不大,梁端附加温度压力增加明显,基本轨位移逐渐减小。
随着简支梁上轨道扣件阻力增加,道岔传力部件作用力增加,尖轨尖端位移和梁轨相对位移有所减小,连续梁上岔板下的凸台纵向力有所减小,简支梁上单元板下凸台影响比较明显。墩台纵向力受影响较小。
② 连续梁桥上扣件阻力影响。
改变连续梁上轨道扣件阻力,选取三种扣件刚度作研究:刚度一为 5 kN/mm,刚度二为16 kN/mm,刚度三为滑移阻力 30 kN/mm。简支梁上仍采用非线性扣件阻力,对轨道结构进行对比分析,计算结果见表5.2-11。
表5.2-11 连续梁上扣件阻力变化的计算结果
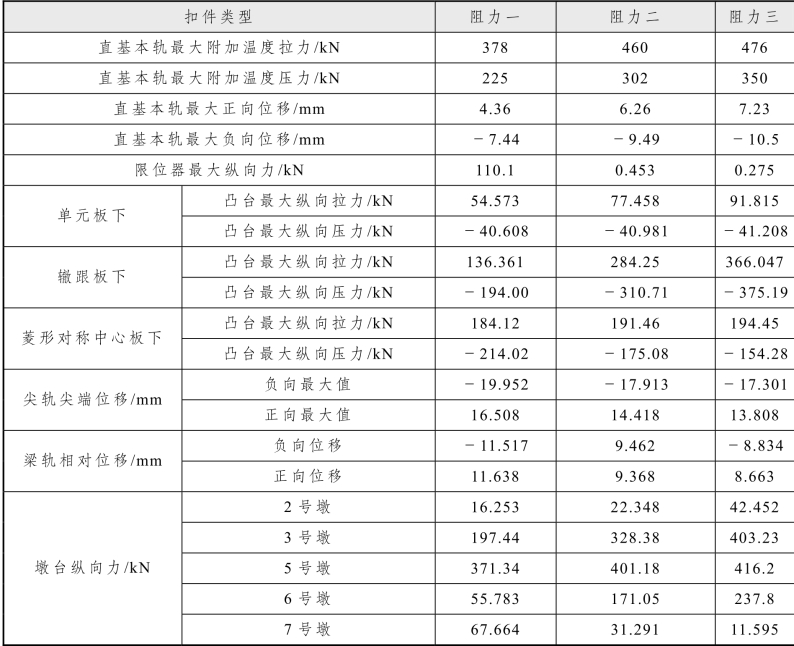
由上表可知:随着连续梁上轨道扣件阻力增加,直基本轨附加纵向力和钢轨位移逐渐增加,其中在轨道板伸缩缝处影响最明显。可见,连续梁上岔区的扣件阻力对钢轨附加纵向力和位移影响很大。
随着连续梁上轨道扣件阻力增加,直基本轨最大附加温度力和位移逐渐增大;限位器纵向力逐渐减小,大部分的纵向力由扣件传递给轨道板,轨道板传递给桥梁,在梁端桥梁把大部分的纵向力传递给钢轨,导致梁端钢轨纵向力增加,限位器纵向力减小;尖轨尖端位移和梁轨相对位移逐渐减小;单元板和辙跟板下凸台的纵向力增加明显,菱形对称中心板下凸台纵向力受影响不大。
随着连续梁上轨道扣件阻力增加,连续梁桥墩纵向力和连续梁相邻的简支梁桥墩纵向力逐渐增加,左边第一跨简支梁固定支座纵向力逐渐增加,右边第5跨简支梁固定支座纵向力逐渐减小。随着连续梁上轨道扣件阻力增加,大部分的纵向力由扣件传递给轨道板,再由轨道板传递给桥梁固定支座,导致桥梁固定支座纵向力增加,其中由于连续梁固定支座布置的影响,左边桥梁固定支座所承受的纵向力较右边的大。
从上述分析可知:改变简支梁上轨道扣件阻力,对简支梁上轨道结构影响明显,而对连续梁上轨道结构影响不大。改变连续梁上轨道扣件阻力,随着连续梁上轨道扣件阻力增加,限位器纵向力逐渐减小,大部分的纵向力由扣件传递给轨道板,再由轨道板传递给桥梁,桥梁把大部分的纵向力传递给钢轨,把小部分的力传递给固定支座,导致梁端钢轨纵向力增加,限位器纵向力减小,固定支座作用力增加。
(3)凸台刚度影响分析。
凸台在德国的无砟轨道技术中得到了广泛的应用。本节改变凸台的纵向阻力,选取 4 种凸台刚度作研究:刚度一为 150 kN/mm,刚度二为 250 kN/mm,刚度三为 600 kN/mm,刚度四为 1 000 kN/mm。其他参数不变,对轨道结构进行对比分析,计算结果见表5.2-12。
表5.2-12 凸台刚度变化的计算结果
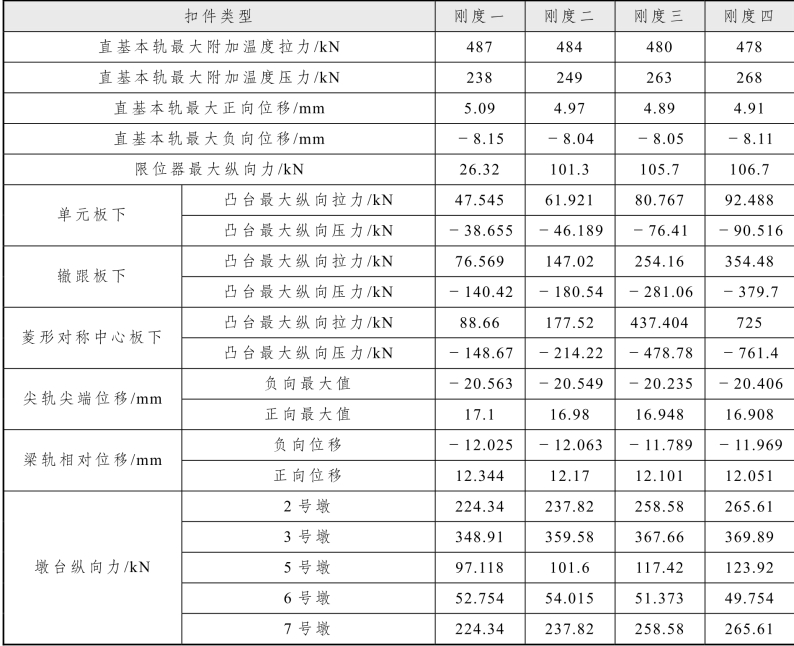
由计算结果可以看出,凸台刚度变化对道岔和桥梁影响不大,仅对凸台纵向力影响较大。凸台胶垫刚度越大,凸台上的纵向力也越大。因此在满足轨道结构设计和胶垫强度的前提下,凸台上胶垫刚度越小越好。
(4)岔区轨道板分块布置影响分析。
桥上岔区轨道板采用凸台基础连接形式,岔区纵向轨道板长度无疑对轨道和桥梁结构会有很大的影响。岔区轨道板的长度及凸台的布置详见图 5.2-30和图5.2-31,荷载工况为钢轨升降温幅度 50 °C、轨道板升降温幅度 30 °C、桥梁升降温幅度20 °C,其他参数不变,对轨道结构进行对比分析。

图5.2-30 布置形式一

图5.2-31 布置形式二
① 直基本轨附加纵向力和位移。
由图5.2-32、图5.2-33可以得知,简支梁上钢轨附加温度力变化不大;连续梁和简支梁的梁缝处,附加温度压力布置形式一较布置形式二大,可见连续梁桥上轨道板长度直接影响钢轨附加温度力和位移的大小,轨道板的长度越长,在轨道板的中部钢轨附加纵向力越大,对钢轨的受力越不利,减小轨道板的长度能有效地增加轨道的稳定性,减小轨道板上钢轨附加力并减小力钢轨位移。
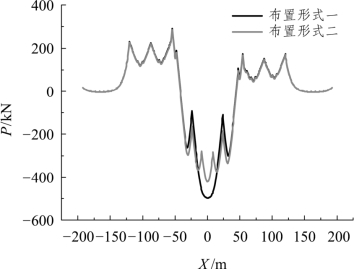
图5.2-32 直基本轨附加纵向力
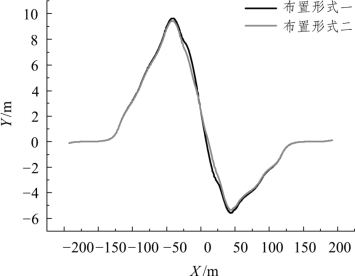
图5.2-33 直基本轨纵向位移
② 道岔传力部件纵向力及可动部分位移。
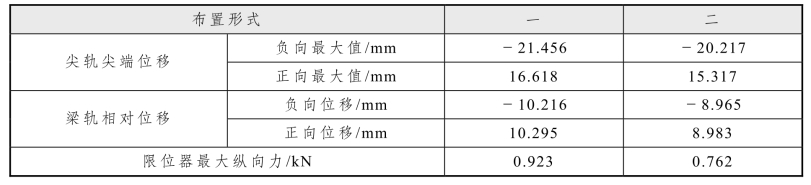
道岔传力部件纵向力和可动部分位移见表 5.2-13。由表可知,布置形式一的道岔传力部件纵向力和道岔可动部分位移较大。可见布置形式二对转辙器更有利。
表5.2-13 尖轨尖端位移和梁轨相对位移
③ 凸台纵向力。
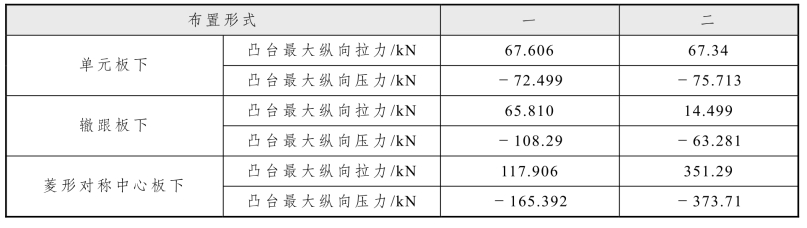
板下凸台纵向力见表 5.2-14,由表可知,改变菱形对称中轴轨道板长度,单元板下凸台纵向力变化不大,菱形对称中心板下凸台纵向力增加明显,辙跟板下凸台纵向力减小。可见,适当减小中轴轨道板的长度,增加中轴轨道板下横向凸台数量,大部分纵向力由中间三块轨道板下凸台承受,能有效减小辙跟板下凸台的受力,减小辙跟轨道板和梁板的相对位移,有利于保证转辙器在桥上正常运转。
表5.2-14 凸台纵向力
④ 桥墩纵向力。
两种道岔板分块方式下墩台纵向力见表5.2-15。由表可知:布置形式一和布置形式二桥墩纵向力相差不大。
表5.2-15 桥墩纵向力/kN

从以上的分析可以得出:采用布置形式二时,菱形对称中轴轨道板长度46.2 m被平均分为三块(每块约 15 m),一定程度上减小了轨道板长度对钢轨附加温度力的影响;中轴轨道板下横向凸台数目的增加,限制了轨道板的位移,有利于控制钢轨爬行;但凸台最大纵向拉压力将明显增加。采用布置形式一钢轨附加温度力及爬行虽较布置形式二略大,但仍在控制范围内,而凸台受力较小。综合理论分析,两种布置方案均可实施,但综合考虑桥梁支座布置方式及施工的便利性,推荐采用布置形式一作为设计实施方案。
5.桥梁结构参数影响分析
桥梁结构的变化对桥上无砟轨道无缝道岔的影响也相当显著,主要的影响因素有桥墩刚度、支座布置形式和桥跨长度。
(1)桥墩刚度影响分析。
桥墩刚度的变化影响着桥梁的伸缩位移,进而影响着桥上无缝道岔的受力和变形。为研究不同桥墩刚度对桥上无缝道岔受力和变形的影响,对简支梁和连续梁分别改变参数,进而对结构进行对比分析。
① 简支梁桥墩刚度影响。
改变简支梁桥墩纵向水平线刚度,分别取刚度一为 40 kN/mm、刚度二为100 kN/mm、刚度三为200 kN/mm进行分析,计算结果见表5.2-16。
表5.2-16 不同简支梁桥墩刚度计算结果
由计算结果可知,随着简支梁桥墩纵向水平线刚度的增加,简支梁固定支座纵向力增加幅度较大,简支梁桥墩纵向水平线刚度增大除对简支梁桥墩纵向力影响较大外,对其他结果影响很小。
② 连续梁桥墩刚度影响。
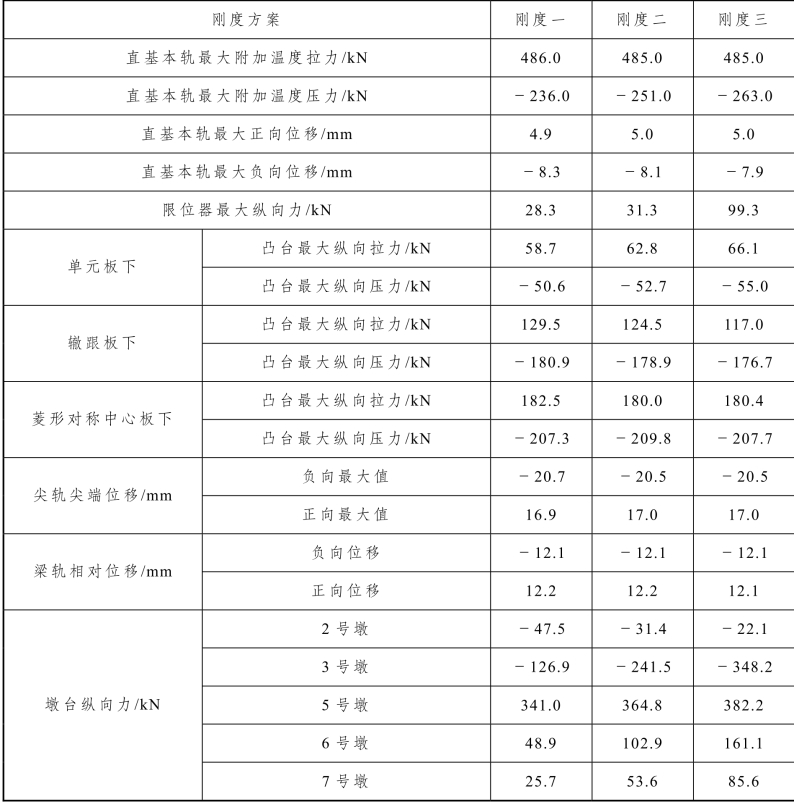
改变连续梁桥墩纵向水平线刚度,分别取刚度一为 100 kN/mm、刚度二为200 kN/mm、刚度三为 500 kN/mm对轨道结构进行对比分析,计算结果见表5.2-17。
表5.2-17 不同连续梁桥墩刚度计算结果
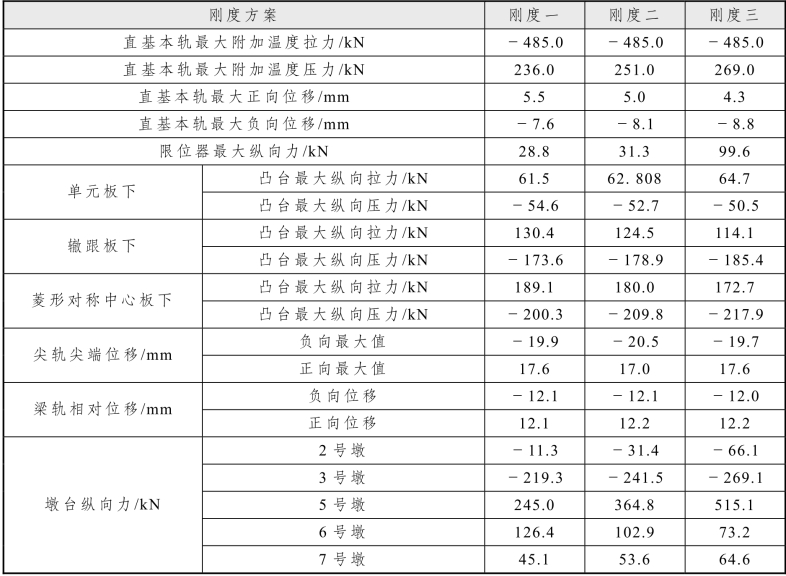
由计算结果可知,随着连续梁桥墩纵向水平线刚度的增加,连续梁固定支座纵向力增加幅度较大,限位器的纵向阻力也随之增大,对其他计算结果影响很小。
③ 支座布置形式影响分析。
桥跨结构支座布置形式的不同,对桥上无缝道岔各部件受力和位移影响也会有差异。由于整个交叉渡线布置在连续梁桥上,连续梁两边为对称结构,所以在讨论过程中,连续梁固定支座位置不变,只改变简支梁上固定支座的位置,其中固定支座的布置形式如图5.2-34~图5.2-37所示,其他参数不变,对轨道结构进行对比分析。

图5.2-34 布置形式一(原定方案)(单位:m)

图5.2-35 布置形式二(单位:m)

图5.2-36 布置形式三(单位:m)

图5.2-37 布置形式四(单位:m)
直基本轨附加纵向力和纵向位移分别见图 5.2-38、图 5.2-39。由图可知,固定支座的布置形式,直接影响直基本轨附加温度力和位移的大小,如布置形式一和布置形式三,布置形式二和布置形式四在连续梁固定支座的左边布置形式是相同的,其附加温度力和位移的变化曲线也是相同的;布置形式二和布置形式三,布置形式一和布置形式四在连续梁固定支座的右边布置形式是相同的,其附加温度力和位移的变化曲线也是相同的。其他计算结果见表5.2-18。

图5.2-38 直基本轨纵向附加力
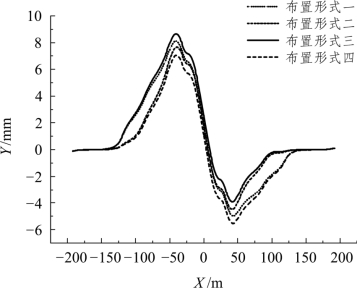
图5.2-39 直基本轨纵向位移
表5.2-18 不同连续支梁桥墩刚度计算结果
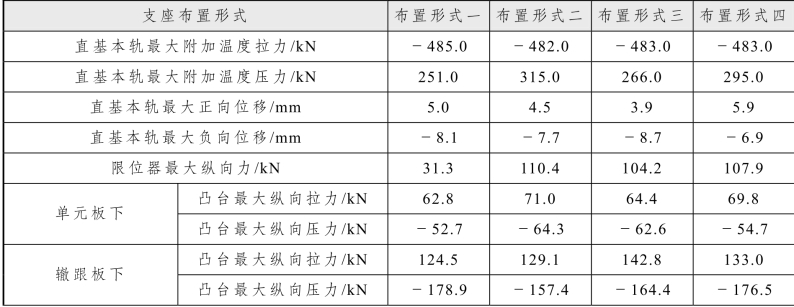
续表
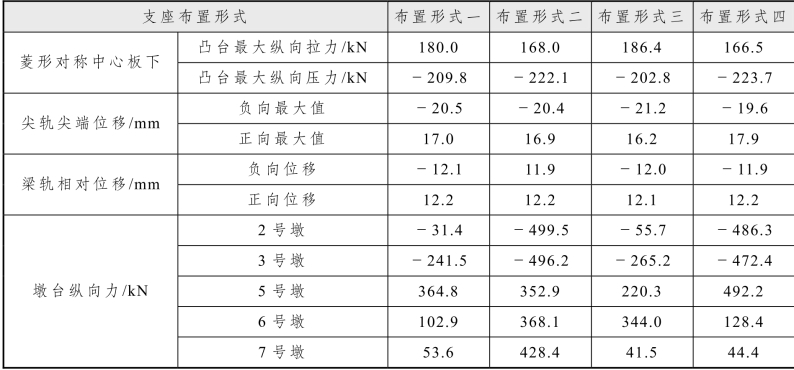
从以上的分析可以得出,改变固定支座的布置方式,对连续梁上道岔尖轨尖端位移、传力部件和凸台受力的影响不大,而对桥墩纵向力影响很大,其中布置方式一和布置方式三的纵向力较布置方式二和布置方式四小很多,而布置方式一较布置方式三整体受力上看更加合理一些。可见选择合理的支座布置方式,对钢轨和桥墩的受力至关重要。
(2)桥跨长度影响分析。
桥梁的伸缩位移随每跨桥梁长度的增加而增加,桥上无缝道岔的受力会产生变化,下面采用两种桥跨布置方式分别进行计算,其桥跨长度和固定支座布置位置如图 5.2-40、图 5.2-41所示,轨道板升温幅度 20 °C,其他参数不变,对轨道结构进行对比分析。

图5.2-40 布置形式一(原定方案)(单位:m)

图5.2-41 布置形式二(单位:m)
直基本轨附加纵向力和位移的变化如图5.2-42所示。由图可知,桥跨长度直接影响钢轨附加温度力和位移的大小,在菱形对称轴左端,布置形式一较布置形式二附加纵向力和钢轨位移大,因为布置形式一连续梁上有效跨度长(32+48)m较布置形式二连续梁上有效跨度(32+32)m要长,所以钢轨的附加温度力和钢轨位移大;在菱形对称轴右端,布置形式一较布置形式二附加纵向力和钢轨位移小,因为布置形式一连续梁上有效跨度长 32 m 较布置形式二连续梁上有效跨度(32+32)m要短,所以钢轨的附加温度力和钢轨位移小。由于受固定支座的影响,布置形式一在菱形对称中轴左边,纵向力和钢轨位移较大;布置形式二纵向力和钢轨位移,以菱形对称中轴为中心成对称分布。
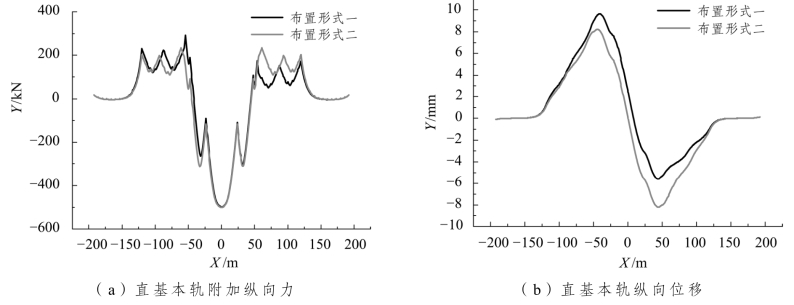
图5.2-42 直基本轨附加纵向力和纵向位移变化
其他计算结果见表5.2-19。
表5.2-19 不同桥梁形式计算结果
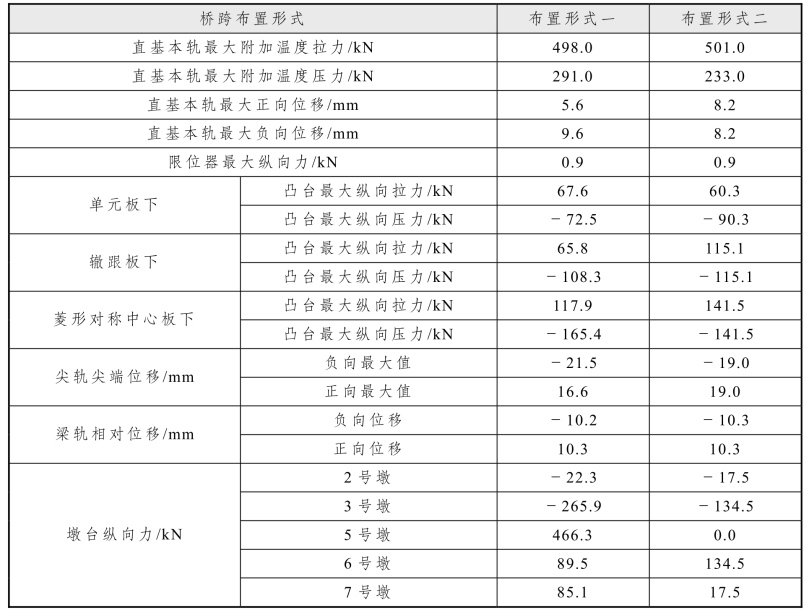
从以上的分析可以得出,改变桥跨长度和固定支座的布置,由于道岔区结构没有发生变化,所以对基本轨最大拉应力、传力部件、尖轨尖端位移和凸台的影响并不大,而对梁端钢轨附加温度力和钢轨位移、桥墩纵向力和支座处桥梁伸缩位移的影响很大。由于交叉渡线轨道结构比较特殊,呈现一种对称式分布,如果采用对称式布置,桥上无缝道岔交叉渡线整体受力更加均匀,其优点体现如下:
① 桥跨长度加长,延长了尖轨尖端至连续梁梁端的距离。桥跨长度由原来的(32+48+32)m 增加到 4×32 m,尖轨尖端至连续梁梁端的距离由原来的13.86 m增加到20.367 m。
② 有效减小了连续梁上温度跨度的长度。温度跨度由原来的(32+48)m减小到(32+32)m,能有效减小钢轨的受力和变形。
由于交叉渡线轨道结构比较特殊,合理选择桥跨长度和支座的布置方式,能有效消除温度跨度的影响,使桥上无缝道岔交叉渡线整体受力更加均匀,有利于桥上无缝道岔交叉渡线长时间地运行。
6.不同基础连接形式对比分析
桥上铺设无砟轨道无缝道岔交叉渡线,桥梁与无缝道岔间的基础连接形式会影响桥梁结构形式、支座布置和无缝道岔的结构设计。由于道岔本身是列车限速的关键设备,存在着较大的结构不平顺,车-岔-桥的耦合作用无疑会增大岔区内轮轨动力响应,严重情况下还有可能引起尖轨及心轨强度储备不足、列车运行平稳性与安全性降低,进而引起列车直侧向过岔时限速,这就要求桥梁结构形式和无缝道岔基础连接形式能够保证桥上无缝道岔的安全运转。根据国内城市轨道交通桥上道岔建设经验,在相同条件下,基础连接形式采用门型钢筋布置和凸台布置,分析桥上无缝道岔交叉渡线无砟轨道受力和变形,并对比分析两种基础连接形式优缺点。
建立计算模型,确定各计算参数以后,对两种不同基础形式的计算模型施加温度荷载。荷载工况:钢轨升降温幅度 50 °C、轨道板升降温幅度 30 °C、桥梁升降温幅度 20 °C。经过计算,得出轨道和桥梁各部件受力和位移情况。
(1)基本轨纵向附加力和纵向位移。
两种不同基础连接形式桥上无缝道岔基本轨纵向力如图5.2-43(a)所示。若采用凸台形式,由于轨道板局部受凸台的约束,大部分可以自由伸缩,基本轨附加力受轨道板的自由伸缩影响比较大。采用门型筋形式,由于轨道板通过门型筋与桥梁牢固地连接在一起,基本轨纵向附加力受桥梁的自由伸缩影响比较大,所以在桥梁板中部呈现一种平缓的变化趋势。由图可知,凸台和门型筋的基本轨最大纵向附加力分别为 309 kN、334 kN。在桥梁的中部,凸台形式钢轨附加纵向力较门型筋形式钢轨附加纵向力大,而在梁端凸台钢轨附加纵向力较门型筋形式钢轨附加纵向力小。从钢轨附加力的角度来看,凸台基础连接形式较门型筋基础连接形式有利。
基本轨纵向位移如图5.2-43(b)所示。由图可知,当基础连接形式为凸台时,基本轨负向最大纵向位移 10.41 mm,正向最大纵向位移 6.2 mm。当基础连接形式为门型筋时,基本轨负向最大纵向位移 11.56 mm,正向最大纵向位移 6.42 mm。通过比较可以得出,凸台形式钢轨纵向位移较门型筋形式钢轨纵向位移小,所以从钢轨伸缩位移的角度来看,凸台基础连接形式较门型筋基础连接形式有利。
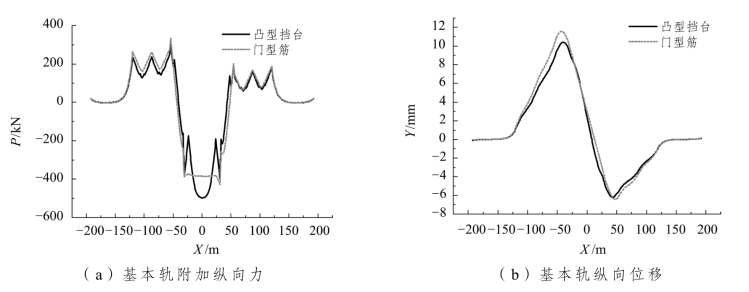
图5.2-43 基本轨附加纵向力和纵向位移变化
(2)道岔传力部件纵向力。
道岔传力部件的受力见表5.2-20所示。
表5.2-20 传力部件受力

由上表可知,当设置两个间隔铁时,凸台形式间隔铁所承受的纵向力较门型筋形式间隔铁所承受的纵向力大。这是因为,凸台形式基础连接形式轨道板受梁约束较门型筋形式基础连接形式轨道板受梁的约束小,轨道板位移较小,导致传力部件的纵向力增加。所以,从传力部件所受纵向力的角度来看,门型筋基础连接形式较凸台基础连接形式有利。
(3)道岔尖轨位移和梁轨相对位移。
尖轨绝对位移和板轨相对位移见表 5.2-21 所示。由表可以看出,凸台形式钢轨尖轨尖端位移较门型筋形式尖轨尖端位移大,凸台形式梁轨相对位移较门型筋形式梁轨相对位移大。在桥上无缝道岔检算过程中,梁轨相对位移是我们所关注的,关系到转辙机在桥上是否能够正常运转。所以,从梁轨相对位移的角度来看,门型筋基础连接形式较凸台基础连接形式有利。
表5.2-21 尖轨位移和梁轨相对位移
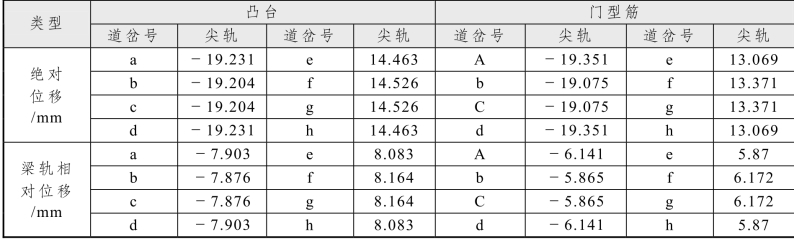
(4)基础连接纵向力和位移。
凸台纵向力分布如图5.2-44所示,当基础连接形式为凸台时,简支梁单元板下凸台纵向力变化范围为-59.222~68.95 kN,连续梁上菱形对称中轴板下凸台纵向力变化范围为-165.39~117.903 kN,辙跟板下凸台纵向力变化范围为-108.29~65.81 kN。单个轨道板下中间凸台纵向力较小,两边凸台所承受纵向力较大。
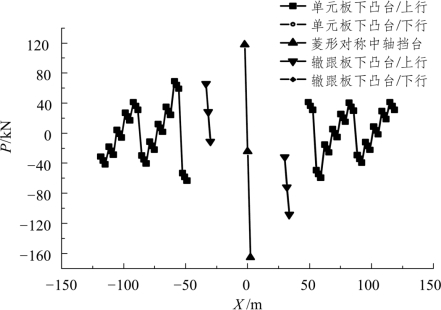
图5.2-44 凸台纵向力
门型筋纵向力分布如图5.2-45所示。当基础连接是门型筋结构时,轨道板下门型筋纵向力变化范围为-625~625 kN,在温度力作用下,轨道板和梁板共同运动,在连续梁上门型筋所承受纵向力较大值出现在轨道板伸缩缝处,在简支梁梁端伸缩缝处门型筋纵向力较桥上轨道板伸缩缝处门型筋纵向力小。

图5.2-45 门型筋纵向力
由于门型筋形式的基础将轨道和桥梁固结,因此在温度变化时,钢筋约束板的位移,梁、板间的相互作用力较大;凸台形式的轨道板的大部分区域可以在桥梁上自由伸缩,可以缓解轨道板和桥梁之间的作用关系。
(5)桥梁支座纵向力和纵向位移。
不同基础连接形式的桥墩纵向力对比见图 5.2-46。由图可知,凸台基础连接形式的墩台纵向力和墩顶纵向位移为门型筋基础连接形式的墩台纵向力和墩顶纵向位移的 83% 左右。从桥梁墩台固定支座所承受的纵向力和墩顶纵向位移的角度来看,凸台基础连接形式较门型筋基础连接形式有利。
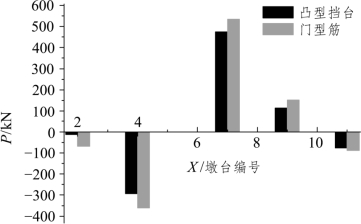
图5.2-46 墩台纵向力
(6)轨道板应力。
凸台和门型筋结构的轨道板应力分别如图5.2-47、图5.2-48所示。由图可知,凸台基础连接形式道岔板和单元板大部分区域第一主应力变化范围为-1.152~1.538 MPa,门型筋基础连接形式道岔板和单元板大部分区域第一主应力变化范围为-1.06~1.728 MPa。

图5.2-47 凸台道岔板和单元板第一主应力云图

图5.2-48 门型筋道岔板和单元板第一主应力云图
由计算结果可知:凸台基础连接形式道岔板和单元板大部分区域上表面等效应力变化范围为7.207~9.223 MPa,门型筋基础连接形式道岔板和单元板大部分区域上表面应力变化范围为 7.333~9.737 MPa;凸台基础连接形式道岔板和单元板下表面凸台区域等效应力变化范围为 7.207~9.223 MPa,门型筋基础连接形式道岔板和单元板大部分区域下表面应力变化范围为2.526~9.737 MPa。
由以上的应力云图可以得知,由于凸台基础连接形式道岔板和单元大部分区域可以在桥梁上自由伸缩,门型筋基础连接形式道岔板和单元板与桥梁固结,所以凸台基础连接形式道岔板和单元板第一主应力和等效应力较门型筋基础连接形式道岔板和单元板第一主应力和等效应力略小。从道岔板和单元板应力的角度来看,凸台基础连接形式较门型筋基础连接形式有利。
综上所述,采用凸台的基础连接形式和门型筋基础连接形式各有优点和缺点,有关受力与位移均满足要求,可结合工程接口情况等优选一种方案作为设计方案。
7.小结
经计算分析,得到以下结论:
(1)直基本轨最大附加温度力出现在连续梁与简支梁梁缝处,桥上道岔板的伸缩缝处会也会出现纵向力峰值,左右的峰值由于固定支座布置的影响存在差异,固定支座的布置方式、桥梁长度和道岔板长度对钢轨的纵向力影响很大。
(2)轨温变化幅度的增加,对直基本轨附加温度拉力、道岔传力部件纵向力、道岔尖轨位移、梁轨相对位移和辙跟板下凸台纵向力影响明显,而对直基本轨附加温度压力、单元板下凸台纵向力、菱形对称中轴板下凸台纵向力和桥墩纵向力影响不大。其中梁轨的温差ΔT=45 °C时,梁轨相对位移仍然没有超出 15 mm 转辙器要求的检算范围,可见转辙器放在轨温变化幅度比较大的地区,仍可以保证其在桥上正常运转。
(3)改变扣件阻力,对简支梁上轨道结构影响明显,而对连续梁上轨道结构影响不大;增大岔区扣件阻力,会减小限位器纵向力,对其他计算结果影响不大,有利于道岔的受力和位移。
(4)凸台刚度变化对凸台纵向力影响较大,但对其他计算结果影响较小,应根据轨道结构强度和凸台周围橡胶强度确定凸台纵向刚度。
(5)桥梁刚度变化对桥墩纵向力影响较大,对其他计算结果影响较小,应综合制动力的影响,设置合理的桥墩纵向刚度。
(6)桥梁温度跨度越小,越有利于道岔和桥梁受力,因此在布置简支梁和连续梁的固定支座时,应尽量选择较小的温度跨度布置方案。
(7)由于交叉渡线是轴对称结构,因此,桥梁布置也应尽量对称,且两者的对称中心相重合最为有利。
(8)桥上岔区轨道板分块布置,菱形对称中轴轨道板长度 46.2 m 被平均分为三块(每块约 15 m),可一定程度上减小轨道板长度对钢轨附加温度力的影响,但凸台所受纵向力较大,设计中应综合考虑。
(9)桥上无缝道岔无砟轨道采用凸台的基础连接形式和门型筋基础连接形式各有优点和缺点,有关受力与位移均满足要求,可择其一实施。
综合分析,建议设计时重点考虑以下方案:
(1)扣件是梁轨之间作用的重要传力部件,其阻力值对轨道结构受力和位移影响很大。经分析,建议岔区扣件阻力采用Ⅲ型扣件,有利于控制轨道结构位移和传力部件受力。
(2)桥上无砟道岔采用门型筋或凸台均可,可根据需要灵活采用。
(3)由于交叉渡线轨道结构对称性很强,结构采用对称式布置对结构的受力和变形很有优势,所以把整个交叉渡线轨道结构布置在 4×32 m 连续梁上较为有利。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




