流体流动阻力的计算方法

( 一) 直管阻力

1.范宁公式 直管阻力，也叫沿程阻力。直管阻力通常由范宁公式计算，其表达式为:

式中:hf——直管阻力，J/kg;

λ——摩擦系数，也称摩擦因数，无量纲;

l——直管的长度，m;

d——直管的内径，m;

u——体在管内的流速，m/s。

范宁公式中的摩擦因数是确定直管阻力损失的重要参数。λ 的值与反映流体湍动程度的Re 及管内壁粗糙程度ε 的大小有关。

2.管壁粗糙程度 工业生产上所使用的管道，按其材料的性质和加工情况，大致可分为光滑管与粗糙管。通常把玻璃管、铜管和塑料管等列为光滑管，把钢管和铸铁管等列为粗糙管。实际上，即使是同一种材质的管子，由于使用时间的长短与腐蚀结垢的程度不同，管壁的粗糙度也会发生很大的变化。

(1) 绝对粗糙度。绝对粗糙度是指管壁突出部分的平均高度，以ε 表示，如图1 -22 所示。表1 -6 中列出了某些工业管道的绝对粗糙度数值。

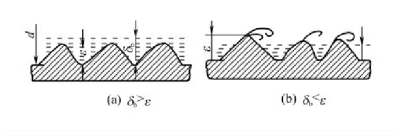
图1-22　管壁粗糙程度对流体流动的影响

表1-6　某些工业管道的绝对粗糙度

(2) 相对粗糙度。相对粗糙度是指绝对粗糙度与管道内径的比值，即ε/d。管壁粗糙度对摩擦系数λ 的影响程度与管径的大小有关，所以在流动阻力的计算中，要考虑相对粗糙度的大小。

3.摩擦系数

(1) 层流时摩擦系数。流体作层流流动时，管壁上凹凸不平的地方都被有规则的流体层所覆盖，λ 与ε/d 无关，摩擦系数λ 只是雷诺数的函数。

上式为哈根—伯稷叶方程，是流体在圆直管内作层流流动时的阻力计算式。

(2) 湍流时摩擦系数。由于湍流时流体质点运动情况比较复杂，目前还不能完全用理论分析方法求算湍流时摩擦系数λ 的公式，而是通过实验测定，获得经验计算式。各种经验公式，均有一定的适用范围，可参阅有关资料。

为了计算方便，通常将摩擦系数λ 对Re 与ε/d 的关系曲线描绘在双对数坐标图上，如图1 -23 所示，该图称为莫狄( Moody) 图。这样就可以方便地根据Re 与ε/d 值从图中查得各种情况下的λ 值。

图1-23　λ 与Re、ε/d 的关系

根据雷诺数的不同，可在图中分出四个不同的区域:

①层流区。当Re ＜2000 时，λ 与Re 为一直线关系，与相对粗糙度无关。

②过渡区。当2000 ＜Re ＜4000 时，管内流动类型随外界条件影响而变化，λ 也随之波动。工程上一般按湍流处理，λ 可从相应的湍流时的曲线延伸查取。

③湍流区。当Re ＞4000 且在图中虚线以下区域时，λ = f( Re，ε/d) 。对于一定的ε/d，λ 随Re 数值的增大而减小。

④完全湍流区。即图中虚线以上的区域，λ 与Re 的数值无关，只取决于ε/d。λ—Re 曲线几乎成水平线，当管子的ε/d 一定时，λ 为定值。在这个区域内，阻力损失与u2 成正比，故又称为阻力平方区。由图可见，ε/d 值越大，达到阻力平方区的Re 值越低。

【例1 -10】20℃的水，以1m/s 速度在钢管中流动，钢管规格为φ60mm×3.5mm，试求水通过100m 长的直管时，阻力损失为多少?

解:从附录三中查得水在20℃时的ρ=998.2kg/m3，μ=1.005 ×10-3Pa·s

d=60 -3.5 ×2 =53mm，l =100m，u=1m/s

取钢管的管壁绝对粗糙度ε =0.2mm，则:

据Re 与ε/d 值，可以从图1 -22 上查出摩擦系数λ=0.03。

( 二) 局部阻力

局部阻力是流体流经管路中的管件、阀门及截面的突然扩大和突然缩小等局部地方所产生的阻力。(www.xing528.com)

流体在管路的进口、出口、弯头、阀门、突然扩大、突然缩小或流量计等局部流过时，必然发生流体的流速和流动方向的突然变化，流动受到干扰、冲击，产生旋涡并加剧湍动，使流动阻力显著增加，如图1 -24 所示。局部阻力一般有两种计算方法，即阻力系数法和当量长度法。

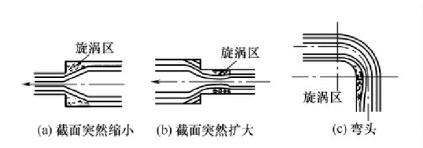
图1-24　不同情况下的流动干扰

1.当量长度法 当量长度法是将流体通过局部障碍时的局部阻力计算转化为直管阻力损失的计算方法。所谓当量长度是与某局部障碍具有相同能量损失的同直径直管长度，用le 表示，单位为m，可按下式计算:

式中:u——管内流体的平均流速，m/s。

le——当量长度，m，

当局部流通截面发生变化时，u 应该采用较小截面处的流体流速。le 数值由实验测定，在湍流情况下，某些管件与阀门的当量长度也可以从图1 -25 查得。

图1-25　管件与阀件的当量长度共线图

2.阻力系数法 将局部阻力表示为动能的一个倍数，则:

式中:ζ——局部阻力系数，无单位，其值由实验测定。

常见的局部阻力系数见表1 -7。

表1-7　常见局部障碍的阻力系数

( 三) 总阻力

管路系统的总阻力等于通过所有直管的阻力和所有局部阻力之和。

1.当量长度法 当用当量长度法计算局部阻力时，其总阻力∑hf 计算式为:

式中: ∑le——管路全部管件与阀门等的当量长度之和，m。

2.阻力系数法 当用阻力系数法计算局部阻力时，其总阻力计算式为:

式中: ∑ζ——管路全部的局部阻力系数之和。

应当注意，当管路由若干直径不同的管段组成时，管路的总能量损失应分段计算，然后再求和。

【例1 -11】20℃的水以16m3/h 的流量流过某一管路，管子规格为φ57mm ×3.5mm。管路上装有90°的标准弯头两个、闸阀(1/2 开) 一个，直管段长度为30m。试计算流体流经该管路的总阻力损失。

解:由附录三查得20℃下水的密度为998.2kg/m3，黏度为1.005mPa·s。

管子内径为d=57 -2 ×3.5 =50mm=0.05m。

水在管内的流速为

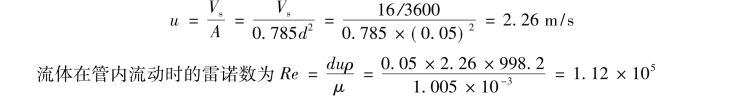
查表取管壁的绝对粗糙度ε =0.2mm，则ε/d =0.2/50 =0.004，由Re 值及ε/d 值查图得λ=0.0285。

(1) 用阻力系数法计算。

查表1 -7 得:90°标准弯头，ζ=0.75;闸阀(1/2 开度) ，ζ=4.5。所以

(2) 用当量长度法计算。

从有关手册查得:90°标准弯头，l/d=30;闸阀(1/2 开度) ，l/d=200。

从以上计算可以看出，用两种局部阻力计算方法的计算结果差别不大，在工程计算中是允许的。

活动建议 分析产生流动阻力的原因，明确计算流动阻力的必要性，取一实际输水管路，进行阻力计算。