现代有轨电车纵向动力学分析模型

（1）列车纵向动力学模型 以一节车辆为例，车辆前后轮轴在同一个平面上并与地面平行。假设列车行驶在一个倾角为β的坡道上。图5-10为车辆动力学模型。

图5-10中，g=9.81m/s²为重力加速度，m为列车质量，v_x为列车纵向速度，F_xf与F_xr分别为前后轮的轮周与地面接触点处的纵向牵引力。

列车运动是列车受到的力与转矩共同作用的结果。轮周的纵向力使其前进或后退。

列车的重力始终作用在车身重心（CG）上。车辆动力学方程为

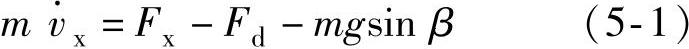
纵向牵引力为前、后轮轴力之和

阻力F_d分为基本阻力和附加阻力，在后文中将详细介绍。

列车的位移为

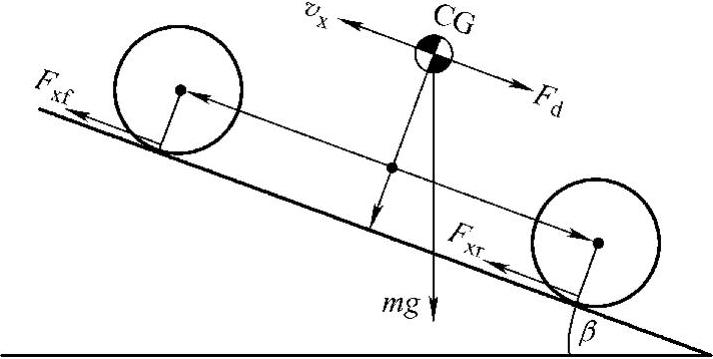
图5-10 车辆纵向动力学模型

（2）列车阻力的计算 阻力分为基本阻力和附加阻力，二者之和为有轨电车受到的总阻力。

1）基本阻力。常用单位基本阻力公式为

列车受到的基本阻力为

其中质量m的单位为t。

公式（5-4）中的常数项“A”与速度无关，可认为是与最大静摩擦力有关。当列车的速度为0时，列车受到的最大静摩擦力为

根据以上分析，可得列车静止与运动时的通用基本阻力公式为

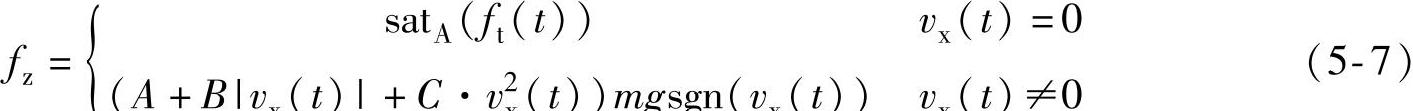
其中，sgn（·）为标准符号函数，sat_A（·）为饱和函数。

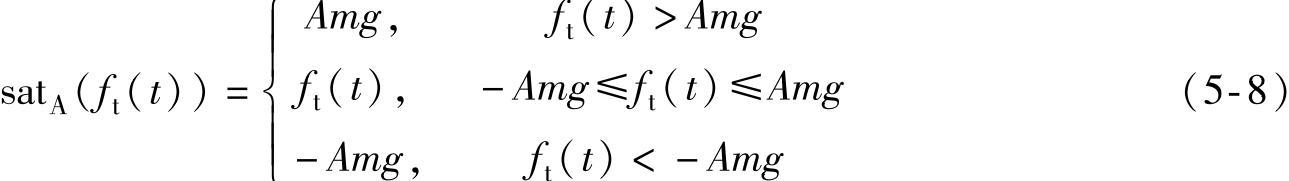
列车的基本阻力是经验公式，它包含了各种因素造成的阻力。

2）附加阻力

①风阻。正面迎风时列车受到的阻力可以用下式表示

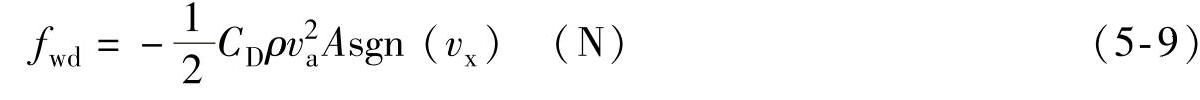
式中C_D——风阻系数；

ρ——空气密度，在20℃以及一个标准大气压下的值大约为1.205kg/m³；

A——列车正面投影面积，m²；

v_a——风速在垂直指向列车正面方向的分量，m/s。(www.xing528.com)

②坡道阻力。列车在坡道上时，重力沿坡道下坡方向的分力形成坡道阻力。根据上、下坡情况的不同，坡道阻力有正负之分。理论上来说负坡道阻力实际上起牵引力的作用。

当列车位于坡度角为β的斜坡上时，重力G可以分为两个分量：垂直分量Gcosβ与平行分量Gsinβ。垂直分量垂直于轨道，并被轨道的反作用力抵消；平行分量与列车运行方向平行，成为由坡道产生的附加阻力。

由于坡道阻力mgsinβ已经在列车运动方程式（5-1）中有描述，因此附加阻力的计算中去除了坡道阻力项。

工程上一般用“坡度”来定义坡道的倾斜程度。通常把坡面的铅直高度和水平宽度的比值叫做坡度，通常用百分数表示。比如，坡度30%是指水平距离上前进了100m的情况下，垂直高度上升了30m。

坡度角与坡度的关系是

式中β——坡度角；

θ——坡度，%。

（3）传动系统 列车采用变频控制策略，牵引电机与轮轴的齿轮齿数比（变速器传动比）为一固定常数。牵引力与牵引电机转矩的关系为

式中F_t——列车轮周牵引力，N；

T_motor——牵引电机转矩，N·m；

i₀——变速器传动比；

r——列车轮周半径，m。

（4）速度控制器 速度控制器的作用是控制牵引电机的转速。它的输入是期望转速和实测转速，通过PI调节器调节，输出牵引电机的期望转矩指令值。电机控制系统作为执行机构根据期望转矩指令值输出相应的牵引转矩，牵引转矩作用于列车，列车开始运行。

速度控制器的输出期望转矩指令值由PI控制器获得

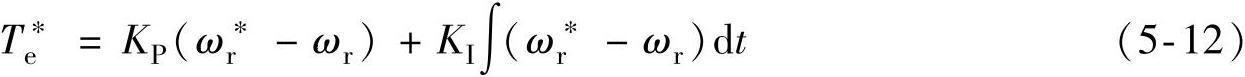
式中K_P、K_I——PI参数；

ω_r^∗、ω_r——分别为期望转速和实测转速，r/m。

期望转速按照列车自动控制系统计算得到的运行曲线查表得到。由运行曲线得到的速度为列车速度（km/h），而速度控制器中的输入速度为电机转速。它们之间的关系为

式中v_x^∗——列车期望速度，km/h。

有轨电车电力牵引系统的电气装置有一定的功率限制，当功率达到最高限制—P时，列车功率将不能再升高。由于功率等于牵引电机转速与转矩的乘积，此时列车如果仍需加速，则需要降低转矩。于是输出转矩等于

其中，

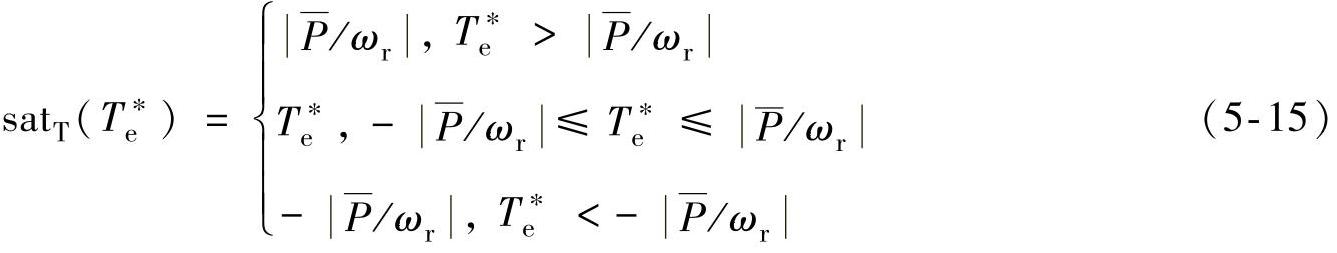
图5-11所示为牵引电机转矩随时间的变化情况，图5-12所示为转矩与列车速度的对应关系。由图中可以看出，列车在36km/h左右进入恒功区，随着列车行驶速度的增加，牵引转矩开始减小。

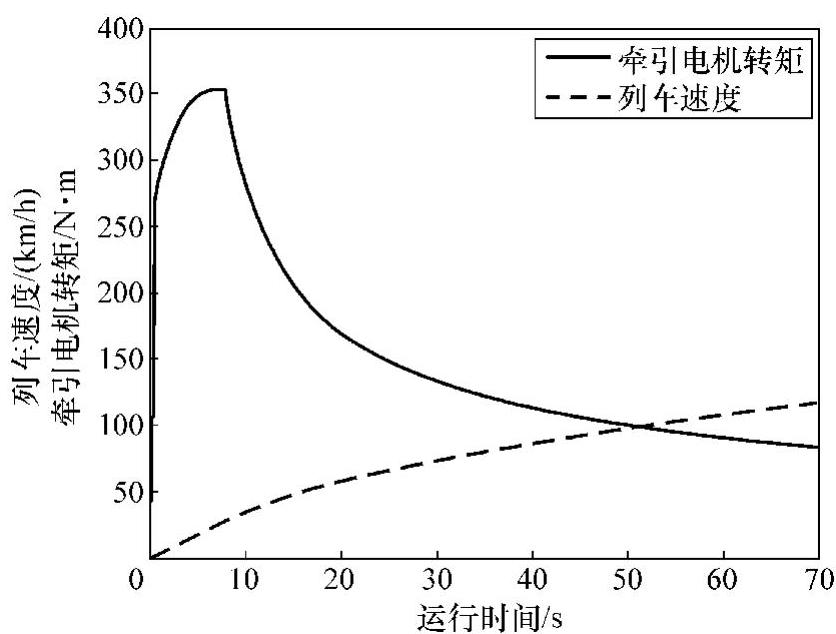
图5-11 牵引电机转矩、列车速度的响应曲线

图5-12 牵引电机转矩—列车速度关系曲线