给排水管道计算-水力规划

1.6.5.1　枝状网水力计算

枝状网的计算比较简单，主要原因是枝状网中每一管段的流量容易确定，只要在每一节点应用节点流量平衡条件qi+∑qij=0，无论从二级泵站起顺水流方向推算，或是从控制点起向二级泵站方向推算，只能得到唯一的管段流量，或者说枝状网只有唯一的流量分配。任一管段的流量确定后，即可按经济流速求出管径，并求得水头损失。此后，选定一条干线，例如，从二级泵站到控制点的任一条干管线，将此干线上各管段的水头损失相加，求出干线的总水头损失，由该水头损失即可求出二级泵站的水泵扬程或水塔高度。这里，控制点的选择很重要，在保证该点水压达到最小服务水头时，整个管网不会出现水压不足的地区。如果控制点选择不当而出现某些地区水压不足时，应重新选定控制点进行计算。

干线计算完成以后，可得出干线上各节点包括接出支线处节点的水压标高（等于节点处地面标高加服务水头）。因此，在计算枝状网的支线时，起点的水压标高已知，而支线终点的水压标高等于终点地面标高与服务水头之和。支线起点和终点的水压标高之差除以支线长度，即得支线的水力坡度，再从支线每一管段的流量并参照此水力坡度，选定相应的管径。

【例题1.6.1】 某城市供水区最高日最高时用水量为0.09375m3/s，要求最小服务水头为157kPa（15.7m）。节点4接某工厂，工业用水量为400m3/d，两班制，均匀使用。城市地形平坦，地面标高5.00m，水管管材按旧钢管考虑。管网布置如图1.6.14所示，试求水塔高度和水泵扬程。

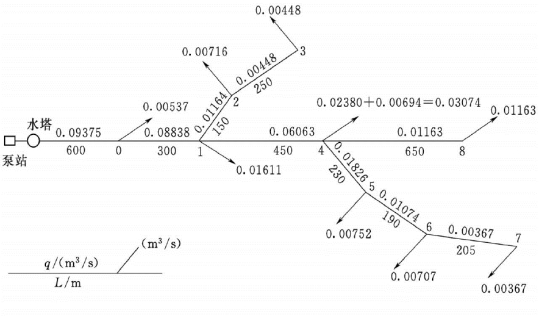
图1.6.14　枝状网计算图

【解】 （1）最高日最高时设计水量：

（2）管线总长度：∑L=3025m，其中水塔到节点0的管段两侧无用户。

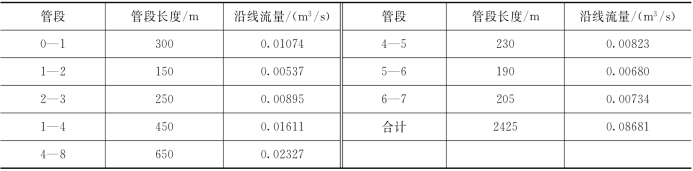
（4）沿线流量Q沿=Lqs见表1.6.3。

表1.6.3　沿线流量计算

（5）节点流量见表1.6.4。

（6）因城市用水区地形平坦，控制点选在离泵站最远的节点8。干管各管段的水力计算见表1.6.5。管径按平均经济流速（表1.6.1）选用。

表1.6.4　节点流量计算

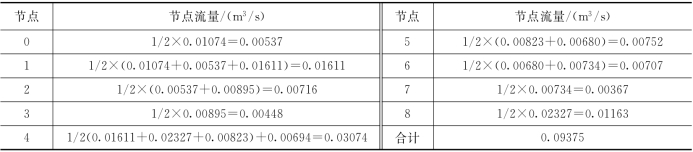
表1.6.5　干管水力计算

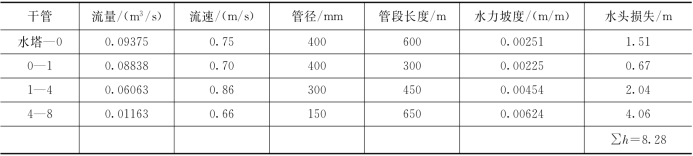
表1.6.5中的水头损失是按海澄威廉公式（1.6.24）计算得到水力坡度i后，乘以管段长度得到的。由表1.6.2查得旧钢管Ch为90～100，本题取95。

（7）干管上各支管接出处节点的水压标高：

节点4：15.70+5.00+4.06=24.76（m）

节点1：24.76+2.04=26.80（m）

节点0：26.80+0.67=27.47（m）

水塔：27.47+1.51=28.98（m）

各支线的允许水力坡度为

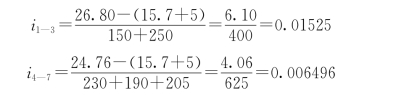
参照水力坡度和流量选定支线各管段的管径和流速，并以此计算管段的水头损失，计算结果见表1.6.6。

表1.6.6　支线水力计算

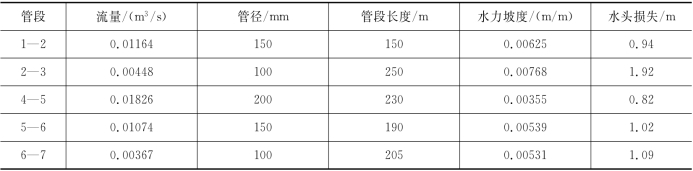
表中管径是参照水力坡度和流量，按照式（1.6.24）计算得到的。参照水力坡度和流量选定支线各管段的管径时，应注意市售标准管径的规格，还应注意支线各管段水头损失之和不得大于允许的水头，例如，支线4—5—6—7的总水头损失为2.93m，而允许的水头损失按支线起点和终点的水压标高差计算为4.06m，符合要求，否则须调整管径重新计算，直到满足要求为止。由于标准管径的规格不多，可供选择的管径有限，所以调整的次数不多。

（8）求水塔高度和水泵扬程。

按水塔高度计算公式：Ht=Hc+hn-（Zt-Zc）得到水塔水柜底高于地面的高度：

水塔建于水厂内，靠近泵站，因此水泵扬程为

上式中3.00m为水塔的水深，4.70m为泵站吸水井最低水位标高，3.00m为泵站内和到水塔的管线总水头损失。

1.6.5.2　环状网水力计算

1.环状网水力计算原理

管网计算目的在于求出各水源节点（如泵采站、水塔等）的供水量、各管段中的流量和管径以及全部节点的水压。

首先分析环状网水力计算的条件。对于任何环状网，管段数P、节点J（包括泵站、水塔等水源节点）和环数L之间存在下列关系：

管网计算时，节点流量、管段长度、管径和阻力系数等已知，需要求解的是管网各管段的流量或水压，所以P个管段就有P个未知数。由式（1.6.25）可知，环状网计算时必须列出J+L-1个方程，才能求出P个流量。

管网计算的原理是基于质量守恒和能量守恒，由此得出连续性方程和能量方程。

所谓连续性方程，就是对于任一节点来说，流向该节点的流量必须等于从该节点流出的流量，如式（1.6.6）所示。式（1.6.6）中的qij值的符号可以任意假定，这里假设离开节点的流量为正，流向节点的流量为负。连续性方程是和流量成一次方关系的线性方程。如管网有J个节点，只可写出类似于式（1.6.6）的独立方程J-1个。因为其中任一方程可从其余方程导出：

能量方程表示管网每一环中各管段的水头损失总和等于零的关系。这里采用水流顺时针方向的管段，水头损失为正，逆时针方向的为负。由此得

式中 Ⅰ，Ⅱ，…，L——管网各环的编号。

如果水头损失用指数公式h=sqn表示时，则式（1.6.27）可写成：

表示管段流量和水头损失的关系，可由h=sqn导出：

式中 下标i、j——表示从节点i到节点j的管段；

Hi、Hj——节点i和j对某一基准点的水压，m；

hij——管段i-j的水头损失；

sij——管段i-j的摩阻。

将式（1.6.29）代入连续性方程（1.6.6）中，得到流量和水头损失的关系如下：

式中 N——连接该节点的管段数。

总括号内的正负号视进出该节点的各管段流量方向而定，这里假定流离节点的管段流量为正，流向节点时为负。

2.环状网计算方法

给水管网计算实质上是联立求解连续性方程、能量方程和管段压降方程。

在管网水力计算时，根据求解的未知数是管段流量还是节点水压，可以分为解环方程、解节点方程和解管段方程三类，在具体求解过程中可采用不同的算法。

解环方程时，哈代-克罗斯（Hardy Cross）法是其中常用的一种算法。由于环状网中，环数少于节点数和管段数，相应的以环方程数为最少，因而成为手工计算时的主要方法。

（2）解节点方程。解节点方程是在假定每一节点水压的条件下，应用连续性方程以及管段压降方程，通过计算调整，求出每一节点的水压。节点的水压已知后，即可以从任一管段两端节点的水压差得出该管段的水头损失，进一步从流量和水头损失之间的关系算出管段流量。工程上常用的算法有哈代-克罗斯法。

解节点方程是应用计算机求解管网计算问题时，应用最广的一种算法。

（3）解管段方程。该法是应用连续性方程和能量方程，求得各管段流量和水头损失，再根据已知节点水压求出其余各节点水压。大中城市的给水管网，管段数多达数百条甚至数千条，需借助计算机才能快速求解。

3.输水管渠计算

从水源到城市水厂或工业企业自备水厂的输水管渠设计流量，应按最高日平均时供水量，并计入输水管（渠）的漏损水量和净水厂自用水量；从净水厂至管网的清水输水管道的设计流量，当管网有调节构筑物时，应按最高日最高时用水条件下，由净水厂负担的供水量计算确定（输水管道的设计水量应为最高日最高时供水量减去由调节构筑物每小时供应的水量）；当无调节构筑物时，应按最高日最高时供水量确定。

上述输水管渠，当负有消防任务时，应分别包括消防补充流量或消防流量。

输水管渠计算的任务时确定管径和水头损失。确定大型输水管的尺寸时，应考虑到具体埋设条件、所用材料、附属构筑物数量和特点、输水管渠条数等，通过方案比较确定。

输水干管不宜少于两条，当有安全储水池或其他安全供水措施时，也可修建一条输水干管。实际工程中，为了提高供水的可靠性，常在两条平行的输水管线之间用连通管相连。输水干管和连通管的管径以及连通管根数，应按输水干管任何一段发生故障时仍能通过事故水量计算确定，城镇的事故水量为设计水量的70%。

以下着重就输水管事故时，如何保证必要的输水量问题进行探讨。

（1）重力供水时的压力输水管。水源在高地时，如果水源水位与水厂处理构筑物水位的高差足够时，可利用水源水位向水厂重力输水。以下研究重力供水时，由n条平行管线组成的输水管系统在事故时所能供应的流量。(www.xing528.com)

设水源水位标高为Z，输水管输水到水处理构筑物，其水位为Z0，这时的水位差H=Z-Z0，称为位置水头，该水头用以克服输水管的水头损失。

假定输水管输水量为Q，平行的输水管线为n条，则每条管线的流量为Q/n。设平行管线的管材、直径和长度相同，并且沿程水头损失按式（1.6.21）计算，则该系统的水头损失为

式中 s——每条管线的摩阻。

当一条管线损坏时，该系统使用其余n-1条管线的水头损失为

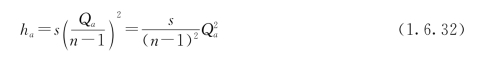
式中 Qa——管线损坏时需保证的流量或允许的事故流量。

因为重力输水系统的位置水头一定，正常时和事故时的水头损失都应等于位置水头，即h=ha=Z-Z0，但是正常时和事故时疏水系统的摩阻却不相等。由式（1.6.31）、式（1.6.32）得事故时流量为

当平行管线数n=2时，则α=（2-1）/2=0.5，这样的事故流量只有正常供水量的一半。如果只有一条输水管，则Qα=0，即事故时流量为零，不能保证不间断供水。

如上所述，实践中为了提高供水可靠性，常采用在平行管线之间增设连接管的方式，这样，当管线某段损坏时，无须整条管线全部停止运行，而只需用阀门关闭损坏的一段进行检修。采用这种措施可以提高事故时的流量。

【例题1.6.2】 设两条平行敷设的输水管线，其管材、直径和长度相等，用2个连通管将输水管线等分成三段，每一段单根管线的摩阻均为s，采用重力供水，位置水头一定。图1.6.15（a）表示输水管线正常工作时的情况，图1.6.15（b）表示一段损坏时的水流情况。求输水管事故时与正常工作时的流量比。

【解】

正常工作时的水头损失为

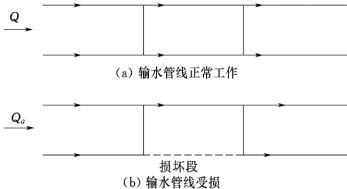
图1.6.15　重力输水系统

某一段损坏时水头损失为

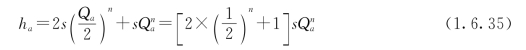
因为连通管的长度与输水管相比很短，所以式中连通管的沿程水头损失和局部水头损失忽略不计。

考虑到采用重力供水，正常时和事故时的水头损失都应等于位置水头，则由式（1.6.34）和式（1.6.35）得到事故时与正常工作时的流量比例为

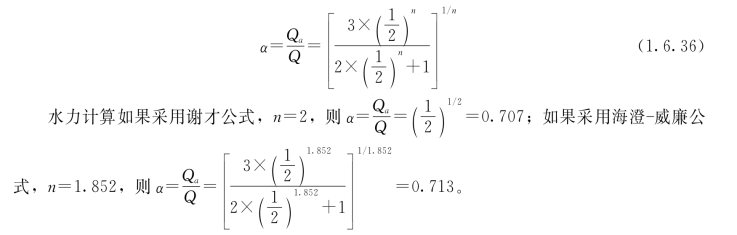
城市的事故用水量规定为设计水量的70%，即要求a≥0.70。所以为满足输水管损坏时的事故流量要求，应敷设两条平行管线，并用连通管将平行管线按总长度至少等分成三段。

（2）水泵供水时的压力输水管。水泵供水时的实际流量，应由水泵特性曲线HP=f（Q）和输水管特性曲线H0+∑（h）=f（Q）求出。设输水管特性曲线中的流量指数n=2，则水泵特性曲线H=f（Q）和输水管特性曲线的联合工作情况如图1.6.16所示：Ⅰ为输水管正常工作时的Q-（H0+∑h）特性曲线；Ⅱ为事故时，当输水管任一段损坏时，阻力增大，使曲线的交点从正常工作时的b点移到a点，与a点相应的横坐标即表示事故时流量Qa。

水泵供水时，为了保证管线损坏时的事故流量，输水管的分段数计算方法如下：

设输水管接入水塔，这时，输水管损坏只影响进入水塔的水量，直到水塔放空无水时，才影响管网用水量。假定输水管Q-（H0+∑h）特性方程表示为

设两条不同直径的输水管用连通管分成n段则任一段损坏时，Q-（H0+∑h）特性方程为

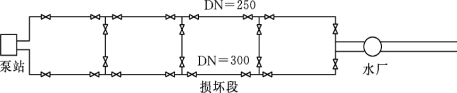
图1.6.16　输水管分段数计算

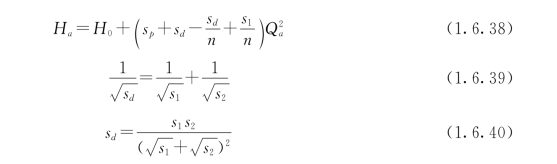
式中 H0——水泵静扬程，等于水塔水面和泵站吸水井水面的高差；

sp——泵站内部管线的摩阻；

sd——两条输水管的当量摩阻；

s1、s2——每条输水管的摩阻；

n——输水管分段数，输水管之间只有一条连通管时，分段数为2，其余类推；

Q——正常时流量；

Qa——事故时流量。

连通管的长度与输水管相比很短，其阻力忽略不计。

输水管任一段损坏时的水泵特性方程为

式中 s——水泵的摩阻。

联立求解式（1.6.41）和式（1.6.42），得到正常工作时水泵的输水流量：

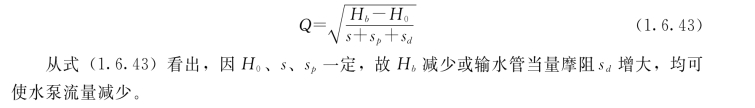
解式（1.6.38）和式（1.6.42），得事故时的水泵输水量：

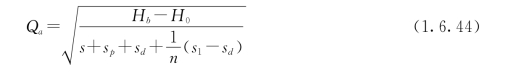
从式（1.6.43）和式（1.6.44），得事故时和正常时的流量比例为

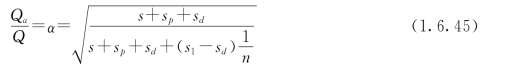
按事故用水量为设计水量的70%，即α=0.7的要求，所需分段数等于：

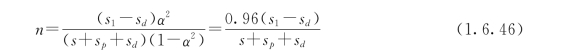
【例题1.6.3】 某城市从水源泵站到水厂敷设两条铸铁输水管（水泥砂浆内衬），每条输水管长度为12400m，管径分别为250mm和300mm，如图1.6.16所示，水泵静扬程40m，水泵特性曲线方程：HP=141.3-2600Q2，式中Q的单位为m3/s。泵站内管线的摩阻sp=210s2/m5。假定DN300输水管线的一段损坏，试求事故水量为70%设计水量时的分段数，及正常时和事故时的流量比。

由式（1.6.40），两条输水管的当量摩阻为

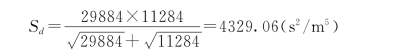
由式（1.6.46），所需要的分段数为

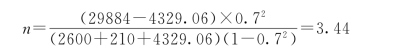
拟分成4段，即n=4，由式（1.6.44），得事故时流量等于：

由式（1.6.43），正常工作时流量为

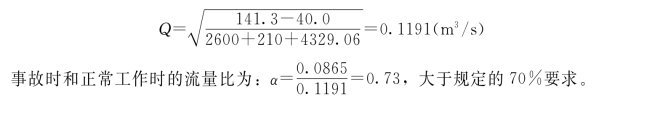
复习思考题

1.城市输配水系统包括哪些组成部分？

2.城市给水管网定线是指什么？定线时应主要考虑哪些问题？

3.何为比流量、沿线流量、节点流量？

4.树状网计算过程是怎样的？

5.树状网计算时，干线和支线如何划分，两者确定管径的方法有何不同？

6.什么叫控制点？每一管网有几个控制点？

7.输水管为什么要分段，如何计算分段数？

8.某城市最高时总用水量为284.7L/s，其中集中供应工业用水量为189.2L/s，干管各管段名称及长度（单位：m）如图1.6.17所示，管段4—5、1—2及2—3为单侧配水，其余为双侧配水，试求：（1）干管的比流量；（2）各管段的沿线流量；（3）各节点流量。

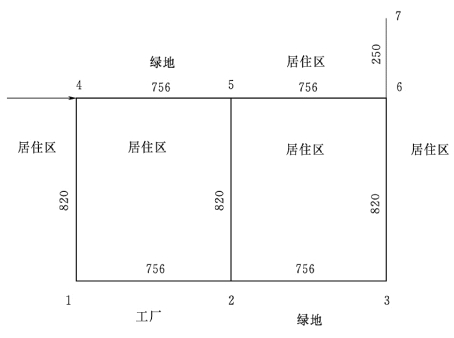
图1.6.17

9.某城镇近期管网规划拟采用树状管网，管网布置示意图如图1.6.18所示，已知该城镇最高时设计用水量为396m3/h，其中大用户集中流量为26.84L/s，分别于5、7节点各取出一半；各管段长度为：L1—2=L1—3=L4—7=800m，L0—1=L1—4=1200m，L4—5=L4—6=900m；其中0—1管段为输水管，4—5管段为单侧配水，其余管段均按双侧配水计。试确定管网各管段的设计流量。

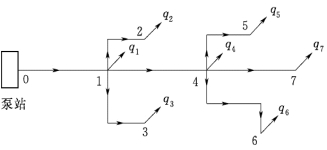
图1.6.18