给排水管道工程技术：管段流量计算

在给水管网的全部管线中，主要是由干管系统所组成。干管的基本任务是沿着主要的供水方向把水送到整个供水区域内。在干管之间的适当位置以连通管连接起来，就构成干管管网；再将干管管网上连接配水管线，就组成了配水管网。这个管网的基本任务是直接供给城市中生活、生产用水以及消防用水。

给水工程总投资中，管网所占的费用很大，一般为70%～80%，因此必须进行多种方案比较，以得到经济合理地满足近期和远期用水的最佳方案。

给水管网的计算就是决定管径和供水时的水头损失。为了确定管径，就必须先确定设计流量。新建和扩建的城市管网按最高时用水量计算，据此求出所有管段的直径、水头损失、水泵扬程和水塔高度（当设置水塔时）。并在此管径基础上，按其他用水情况，如消防时、事故时、对置水塔系统在最大转输时各管段的流量和水头损失，从而可以知道按最高用水时确定的管径和水泵扬程能否满足其他用水时的水量和水压要求。本节所要解决的就是通过管网的流量、每段管子的管径和管段的水头损失3个问题。

1.6.2.1　沿线流量

给水管网在工作时，水不断地从干管管网流向配水管网，同时沿线向两边供水，因干管和分配管上接出许多用户，水管沿线既有工厂、机关、旅馆等大量用水的单位，也有数量很多但水量较少的居民用水，沿管线配水，情况比较复杂。现取出配水管网上的一段管路，干管配水情况如图1.6.6所示，向两旁用户供水，沿线有数量较多的用户用水q1，q2，…，qn等，每个配水点的流量qi并不大，同时流量也不固定，在不同时间内水量变化很大，因此，管网真实情况确实很复杂。还有分配管的供工厂、机关等大用水户的集中流量Q1，Q2，Q3，…，Qn等，如图1.6.6所示。各用户用水量大小不等，用水高峰不同时出现，各户用水大小随时间变化，所以在干管管网上每一管段的配水情况都是极其复杂的。

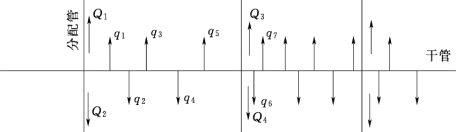
图1.6.6　干管配水情况

如果按照实际用水情况来计算管网，非但不可能，并且因用户用水量经常变化也没有必要。因此，计算时往往加以简化，即假定用水量均匀分布在全部干管上，由此算出干管线单位长度的流量，称为比流量：

式中 qs——比流量，L/（s·m）；

Q——管网供水的总流量，L/s；

∑q——管网供应大用户集中流量的总和，L/s；

∑l——配水的干管有效长度，m，不供水的管段不计算在内，单侧供水的管子只算一半长度，经过无建筑的地区、广场、公园等不予计算管长。

从式（1.6.1）看出，干管的总长度一定时，比流量随用水量增减而变化，最高用水量和最大转输时的比流量不同，所以在管网计算时须分别计算，城市内人口密度或房屋卫生设备条件不同的地区，也应该根据各区的用水量和干管线长度，分别计算其比流量，以得出比较接近实际用水的结果。

有了比流量qs就可以计算某一管段的配水流量，称之为“沿线流量”。从比流量求出各管段沿线流量的公式如下：

式中 ql——沿线流量，L/s；

l——该管段的长度，m。

整个管网的沿线流量总和∑ql，等于qs∑l。从式（1.6.1）可知，qs∑l值等于管网供给的总用水流量减去大用户集中用水总流量，即等于Q-∑q。

但是，按照用水量全部均匀分布在干管上的假定，以求出比流量的方法，存在一定的缺陷。因为它忽视了沿线供水人数和用水量的差别，所以与各管段的实际配水量并不一致。为此提出另一种按该管段的供水面积决定比流量的计算方法，即将式（1.6.1）中的管段总长度应用供水区总面积∑A代替，得出的是以单位面积计算的比流量qA。这样，任一管段的沿线流量，等于其供水面积和比流量qA的乘积。供水面积可用等分角线的方法来划分街区。在街区长边上的管段，其两侧供水面积均为梯形；在街区短边上的管段，其两侧供水面积均为三角形。如图1.6.7所示，管段1—2负担的面积为A1+A2；如图1.6.8所示，管段3—4负担的面积为A3+A4。这种方法虽然比较准确，但计算较为复杂，对于干管分布比较均匀、干管间距大致相同的管网，并无必要按供水面积计算比流量。

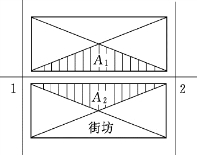
图1.6.7　按对角线划分供水面积

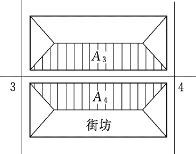
图1.6.8　按等分角线划分供水面积

1.6.2.2　节点流量

管网中管段的流量，由两部分组成：一部分是沿该管段长度l配水的沿线流量ql，另一部分是通过该管段输水到以后管段的转输流量qt。转输流量沿整个管段不变，而沿线流量由于管段沿线配水，所以管段中的流量顺水流方向逐渐减少，到管段末端只剩下转输流量。如图1.6.9所示，管段1—2起端1的流量等于转输流量qt加沿线流量ql，到末端2只有转输流量qt，因此每一管段从起点到终点的流量是变化的。对于流量变化的管段，难以确定管径和水头损失，所以有必要将沿线流量转化成从节点流出的流量。这样，沿管线不再有流量流出，即管段中的流量不再沿管线变化，就可根据该流量确定管径。

沿线流量转化成节点流量的原理是求出一个沿线不变的折算流量q，使它产生的水头损失等于实际上沿线变化的流量qx产生的水头损失。

图1.6.9中的水平虚线表示沿线不变的折算流量q：

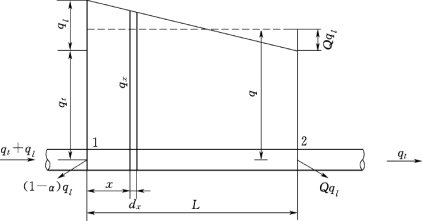
图1.6.9　沿线流量折算成节点流量

式（1.6.4）中α称为折算系数，是把沿线变化的流量折算成在管段两端节点流出的流量，即节点流量系数。按沿线流量转化成节点流量的原理，经推导，可得到折算系数：

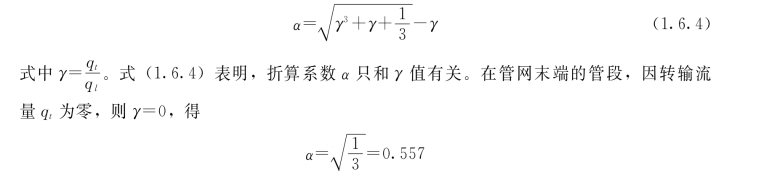
如果γ=0，即转输流量远大于沿线流量的管段（在管网的起端），折算系数为

(www.xing528.com)

由此可见，因管段在管网中的位置不同，γ值不同，折算系数α值也不等。一般而言，在靠近管网起端的管段，因转输流量比沿线流量大得多，α值接近0.5；相反，靠近管网末端的管段，α值大于0.5。通常为了便于管网计算，统一采用α=0.5，即将沿线流量折半作为管段两端的节点流量，解决工程问题时，已足够精确。

因此，管网任一节点的节点流量为

即任一节点的节点流量qi等于与该节点相连各管段的沿线流量ql总和的一半。

城市管网中，工业企业等大用水户所需流量，可直接作为接入大用水户的节点流量。工业企业内的生产用水管网，用水量大的车间，用水量也可以直接作为节点流量。

这样，管网图上只有集中在节点的流量，包括由沿线流量折算的节点流量和大用水户的集中流量。管网计算中，节点流量一般在管网计算图的节点旁引出箭头注明，以便于进一步计算。

1.6.2.3　管段计算流量

求出节点流量后，即可进行管网的流量分配，分配到各管段的流量已经包括了沿线流量和转输流量。求出各管段流量后，即可根据该流量确定管径和进行水力计算，所以流量分配在管网计算中是一个重要环节。

1.枝状网

以图1.6.10单水源的枝状网为例。图中从水源（二级泵站，高地水池等）供水到枝状网各节点的水流方向只有一个，如果任一管段发生事故时，该管段以后的地区就会断水，因此任一管段的流量等于该管段以后（顺水流方向）所有节点流量的总和。

例如，图1.6.10中管段3—4的流量为

可以看出，枝状网的流量分配比较简单，各管段的流量容易确定，并且每一管段只有唯一的流量值。

图1.6.10　枝状网流量分配

2.环状网

环状网的流量分配比较复杂。因各管段的流量与以后各节点流量没有直接的联系。但环状网流量分配时必须保持每一节点的水流连续性，也就是流向任一节点的流量必须等于流离该节点的流量，以满足节点流量平衡的条件，用公式表示为

式中 qi——节点i的节点流量；

qij——从节点i到节点j的管段流量。

假定离开节点的管段流量为正，流向节点的为负。

则以图1.6.11的节点1为例：离开节点的流量为q1、q1-2、q1-4，流向节点的流量为Q，因此根据式（1.6.6）得

可以看出，对节点1来说，即使进入管网的总流量Q和节点流量q1已知，各管段的流量，如q1-2和q1-4等值，还可以有不同的分配，即有不同的管段流量。假设在分配流量时，对其中的一条，例如管段1—2分配很大的流量q1-2，而另一管段1—4分配很小的流量q1-4，因Q1-2+q1-4仍等于Q-q1，即保持水流的连续性，这时敷管费用虽然比较经济，但明显和安全供水产生矛盾。因为当流量很大的管段1—2损坏需要检修时，全部流量必须在管段1—4中通过，使该管段的水头损失过大，从而影响到整个管网的供水量或水压。

因此，环状网流量分配时，应同时考虑经济性和可靠性。经济性是指流量分配后得到的管径，应使一定年限内的管网建造费用和管理费用为最小。可靠性是指能向用户不间断地供水，并且保证应有的水量、水压和水质。很清楚，经济性和可靠性之间往往难以兼顾，一般只能在满足可靠性的要求下，力求管网最为经济。

环状网流量分配的步骤是：

（1）按照管网的主要供水方向，先拟定各管段的水流方向，并选定整个管网的控制点。控制点是管网正常工作时和事故时必须保证所需水压的点。

（2）为了可靠供水，从二级泵站到控制点之间选定几条主要的平行干管线，这些平行干管中尽量均匀分配流量，并且符合水流连续性即满足节点流量平衡的条件。这样一条干管损坏，流量由其他干管转输时，不会使这些干管中的流量增加过多。

（3）与干管垂直的连接管，其作用主要是沟通平行干管之间的流量，有时起到一定的输水作用，有时只是就近供水到用户，平时流量一般不大，只有在干管损坏时才转输较大的流量，因此连接管中可分配较少的流量。

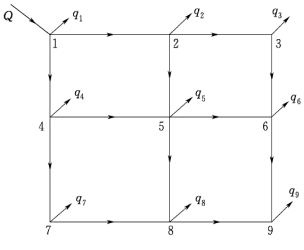
图1.6.11　环状网流量分配

多水源管网，应由每一水源的供水量定出其大致供水范围，初步确定各水源的供水分界线，然后从各水源开始，循供水主流方向按每一节点符合qi+qij=0的条件，以及经济和安全供水的考虑，进行流量分配。位于分界线上各节点的流量，往往由几个水源同时供给。各水源供水范围内的全部节点流量加上分界线上由该水源供应的节点流量之和，应等于该水源的供水量。

环状网流量分配后即可得出各管段的计算流量，由此流量即可确定管径。