新能源汽车电机设计及弱磁控制系统仿真

为了提高控制性能，将有限元软件分析得到的不同工况下的电机变化参数应用在控制系统中，系统框图如图6-28所示。将随电流非线性变化的电感参数用在解耦控制和电流控制算法中，有效改善了磁路饱和引起的电压控制器饱和与控制系统瞬态不稳定等问题。

在控制系统中，利用非线性插值的方法对电机的磁路饱和影响进行补偿，并对其系统仿真结果进行分析。图6-29～图6-32所示为电机从转速零达到最大转速的系列仿真图。图6-29所示为机端电压矢量轨迹和电机磁链圆，随着电机转速从零开始增加，电压圆半径逐渐增大；电机转速达到转折转速后，机端电压达到极限值形成圆形且保持半径不变。磁链圆因电机的弱磁率特性不同而不同，随之速度增加磁链圆逐渐缩小，当电机达到最大速度后，去磁电流i_d为电流极限值，i_q几乎为零，电机磁链圆为半径恒定的圆环。图6-30所示为电机的转速和转矩波形图，在恒转矩区，转速增加，转矩几乎不变；在弱磁区，随着速度增加，则以牺牲转矩为代价保持功率不变，转速达到最大时转矩输出为零。整个速度范围的dq轴电流和电压变化波形图如图6-31和图6-32所示。

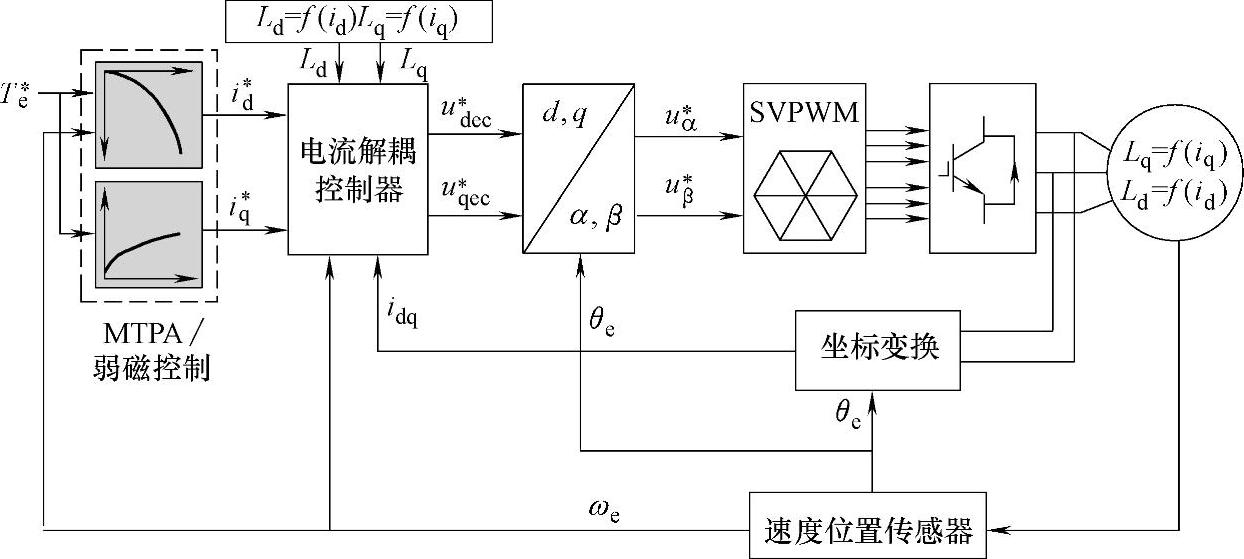
图6-28 非线性插值补偿磁路饱和影响的系统框图

图6-33所示为机端电压跟随控制器电压波形图。在控制系统中用插值方法对电机的磁路饱和影响进行了补偿，从图中可看出补偿后比没有补偿的拓宽了弱磁区速度运行范围，提高了恒转矩区输出转矩，更好地解决了恒功率区电机机端电压超过限制电压而产生的控制系统不稳定，同时提高了控制系统动态性能、鲁棒性和控制精度。但是这种方法不具有通用性，是以已知不同工况下电机的参数变化值为前提的。随着电机老化和温度场变化等因素的影响，电机参数测量值仍与运行中的电机参数存在误差，在高精度控制领域这种方法并不是完美的。因此，只有将在线获取的时变参数应用在控制系统中才能使控制精度更高，控制效果更好。

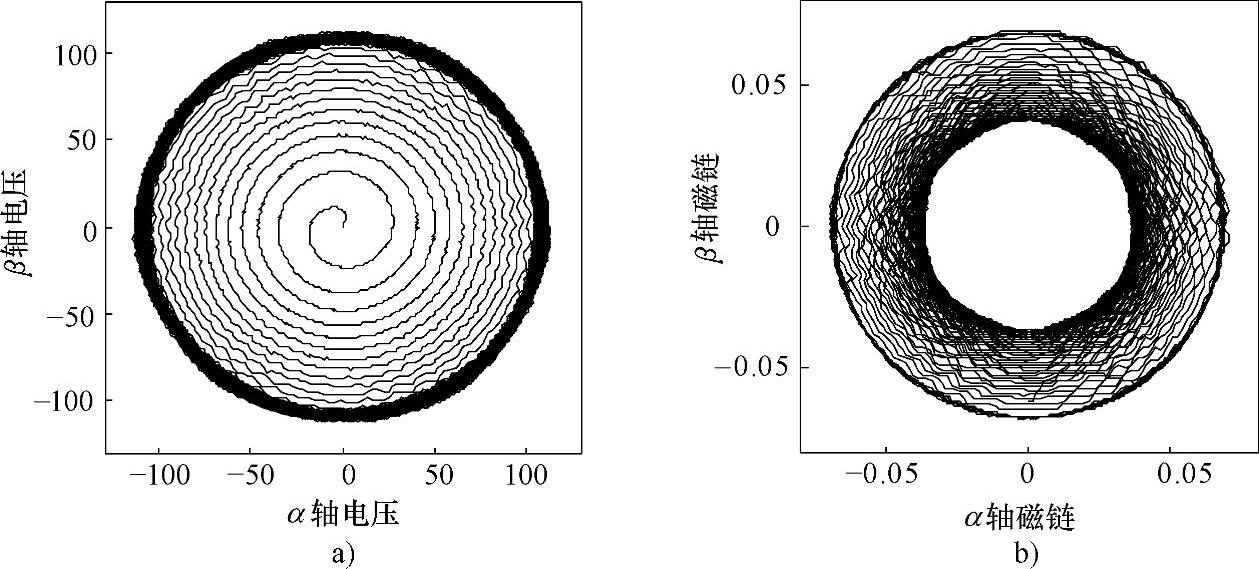
图6-29 插值补偿饱和影响的电机电压圆和磁链圆

a）电压圆 b）磁链圆

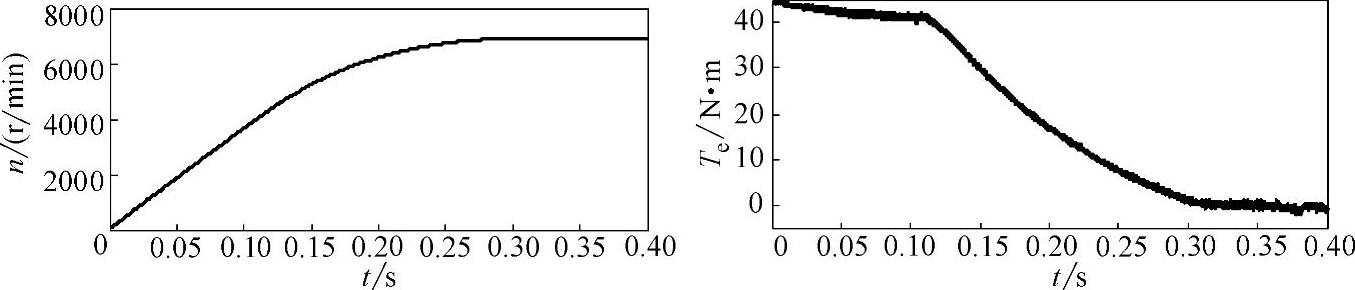
图6-30 插值补偿饱和影响的转速和转矩波形图(www.xing528.com)

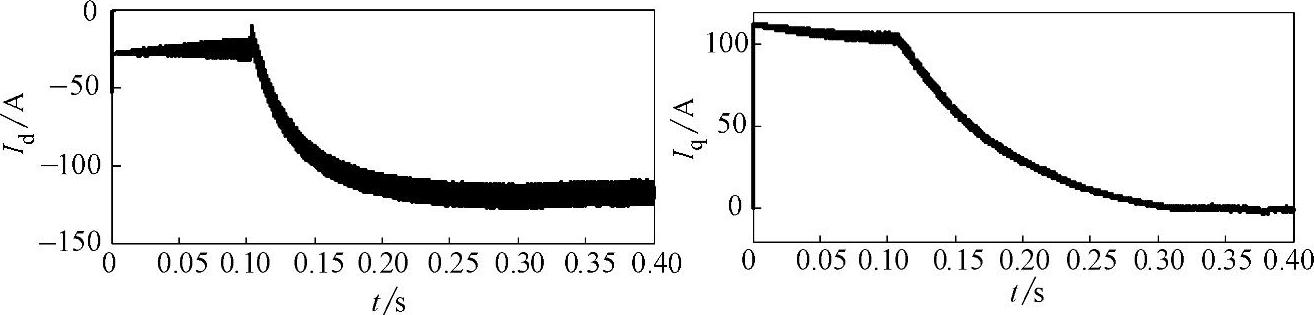
图6-31 插值补偿饱和影响的dq轴电流波形图

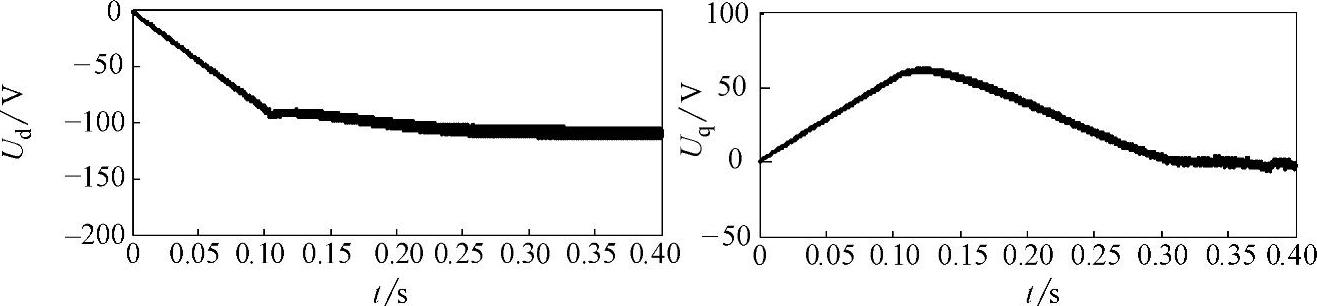
图6-32 插值补偿饱和影响的dq轴电压波形图

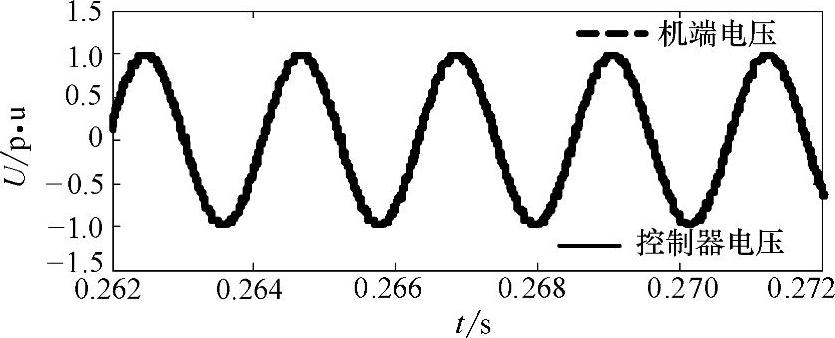
图6-33 机端电压跟随控制器电压波形图

磁路饱和补偿和无磁路饱和补偿的转矩—速度特性比较如图6-34所示。

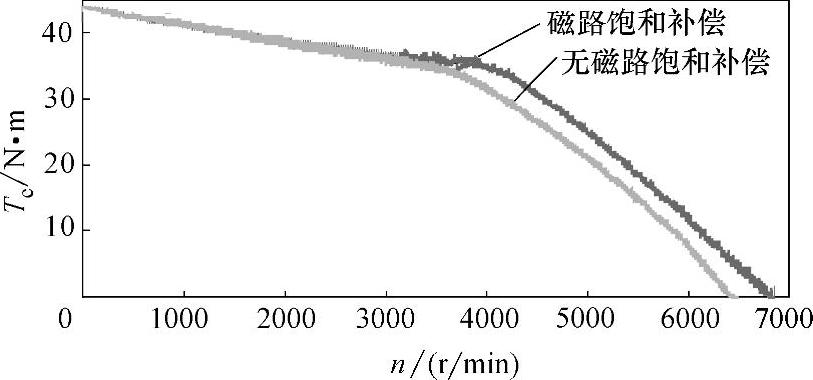
图6-34 转矩—速度特性比较