永磁转子结构抑制纹波转矩于新能源汽车电机设计及弱磁控制

纹波转矩主要是由于感应电动势谐波和定子电流谐波相互作用产生的，因此在电机设计过程中，应当尽量地消除谐波。由转子磁通势的对称性可知，转子气隙磁通密度除基波外只有奇次谐波，且对于三相电机来说，定子气隙磁通密度没有3及3的倍数次谐波。所以，只有定、转子气隙磁通密度谐波同为6m±1次时才能产生纹波转矩^[25]。

对B_s和B_r进行傅里叶展开后得到纹波转矩纹波与平均转矩比值为

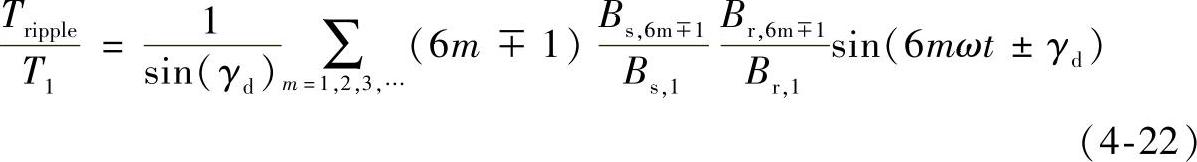
其中，B_s和B_r的基波分量的旋转方向相同，且B_r的各次谐波旋转方向与基波相同。但是，对于B_s来说，6m+1次谐波旋转方向与基波相同，6m-1次谐波旋转方向与基波相反。

式（4-22）说明纹波转矩是由定、转子磁通密度谐波相互作用的结果，即只有定子与转子有相同谐波即同为6m±1磁通密度时才会产生纹波转矩，同时纹波转矩的大小与定、转子磁通密度相对应的谐波次数成正比，因此，高次谐波更容易产生较大的纹波转矩。所以必须减少定、转子之间相同谐波的相互作用及高次谐波次数，才可减少纹波转矩。

这里设定转子结构尺寸及绕组形式一定，转子结构采用V形永磁体结构。在额定负载情况下从转子磁通密度入手，通过对其V形永磁体结构中关键尺寸的优化来改变转子永磁体磁通密度，进而减少定、转子磁通密度和其相对应的谐波次数三者的乘积来减少纹波转矩。

图4-46所示为参考文献[16]中未经优化的V形转子内置式永磁同步电机的1/4个模型，该结构有三个主要参数：磁钢厚（T）、磁钢宽（W）和V形张角（α）。这里将在此转子结构的基础上，通过对转子主要参数的优化实现纹波转矩最小化。

由于永磁体磁导率接近真空磁导率，磁钢厚T的大小直接决定了等效气隙的分布，进而影响d轴电感及电机的凸极率；磁钢宽W主要决定了永磁体磁链的大小，永磁磁链随着W的增大而增大。磁钢厚T和磁钢宽W决定了永磁体的用量，也会影响输出的平均转矩。因此，不能通过对这两个参数的调整和优化来抑制纹波转矩。

V形永磁体张角α决定了转子气隙磁通密度在空间的分布，进而影响了气隙磁通密度波形中各次谐波的含量。在一定范围内，其角度的大小既不会影响永磁体用量也不会影响平均转矩的大小。

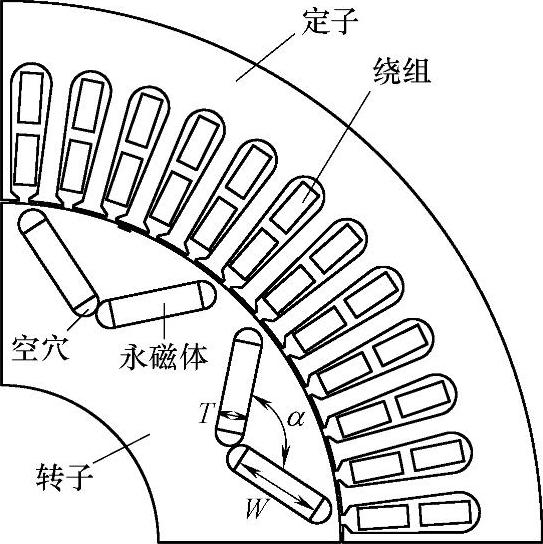
图4-46 优化前V形转子内置式永磁同步电机模型

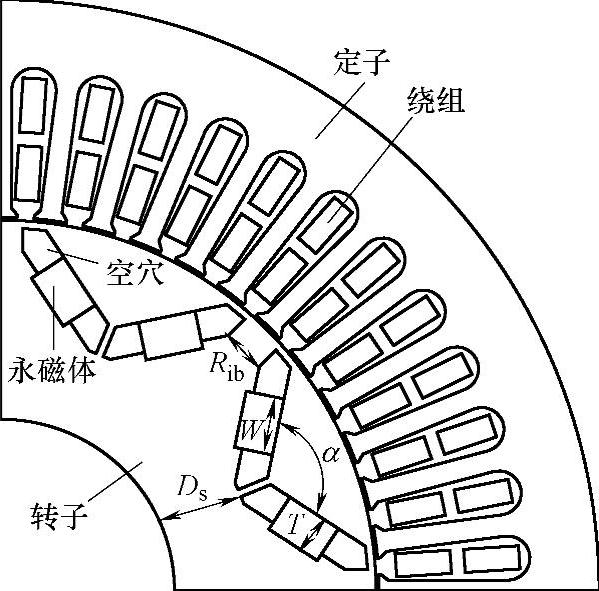
图4-47 优化后V形转子内置式永磁同步电机模型

这里在图4-46所示的转子结构的基础上，提出了一种优化的V形永磁体转子结构，其1/4电机模型如图4-47所示。该转子结构中每极包含两个空穴，通过V字中间的连通部分增强了转子机械强度，电机高速旋转时的安全性有了保证。其次，永磁体的宽度要大于空穴的宽度，磁间桥宽度固定，在保证固定住永磁体的同时也有效地防止漏磁。

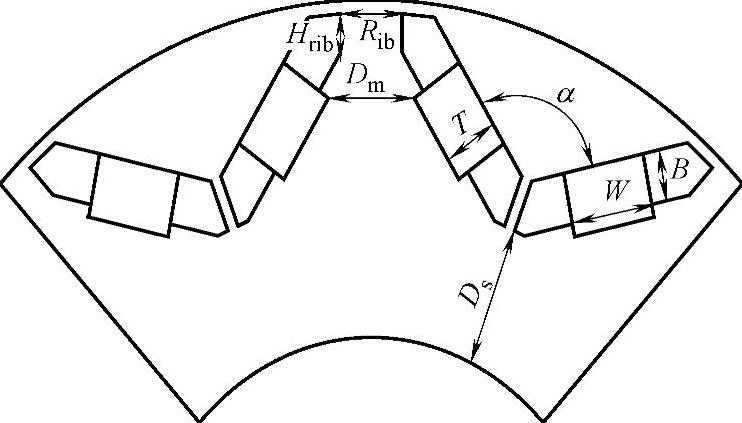
为了更加细化地分析V形永磁体张角α对纹波转矩的影响，将其拆分为若干个长度来代替角度α。图4-48标出了该转子的各个主要参数。从中可以看出，V字形张角α主要由长度参数D_s和R_ib决定。其余各个主要参数的值如表4-18所示。

(www.xing528.com)

图4-48 优化后V形永磁体转子各主要参数

表4-18 优化后V形永磁体转子拓扑尺寸

为了验证随着V形永磁体张角α的变化对纹波转矩的影响，同时考虑到转子内部空间的限制，这里设定D_s的变化范围为9～13mm，R_ib的变化范围为5.1～5.7mm。从而由D_s和R_ib共同决定的张角α的变化范围为100°～126°。

设定的电机运行状态为：负载角等于42°，转子初始位置角等于26.25°，定子相电流等于6A，转速为基速1000r/min。经有限元仿真验证的纹波转矩含量随着D_s和R_ib的变化关系如表4-19所示。从中可看出，当R_ib=5.7mm、D_s=12mm时纹波转矩含量最小，为5.65%，相比于优化前的V形永磁体结构的电机，纹波转矩含量下降了近14%。图4-49所示为转子结构优化前和优化后的有限元仿真纹波转矩波形的对比，此时优化后的V形永磁体张角α为118°。

需要注意的是，该模型优化前和优化后的齿槽转矩峰值均小于0.3N·m，如图4-50所示，相比于14.3N·m的平均输出转矩可以忽略，进而通过有限元仿真得出的脉动转矩波形可近似认为是纹波转矩波形。

表4-19 随关键尺寸变化的纹波转矩含量有限元解

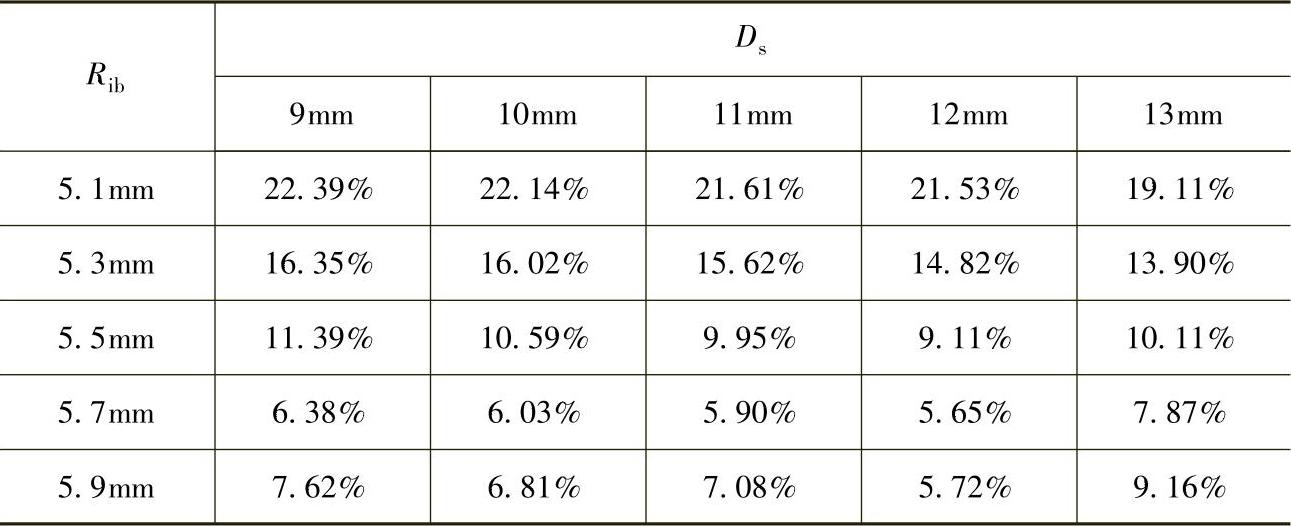
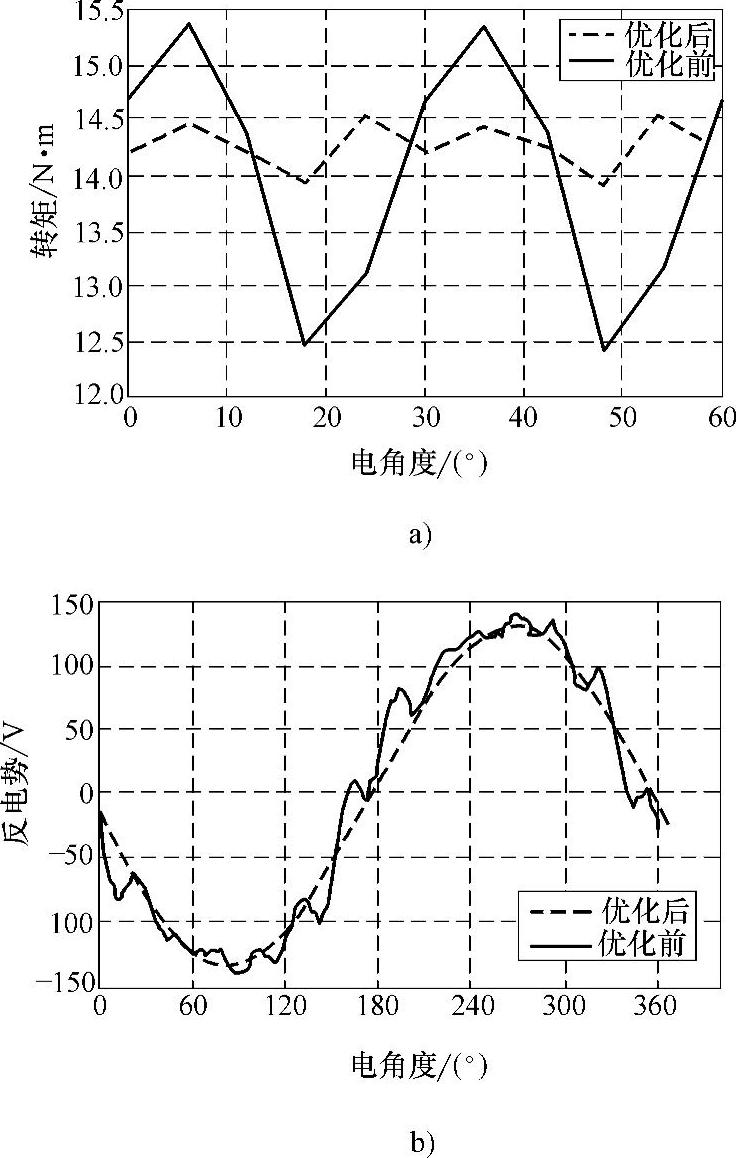
图4-49 优化前后纹波转矩和反电动势

a）纹波转矩 b）反电动势

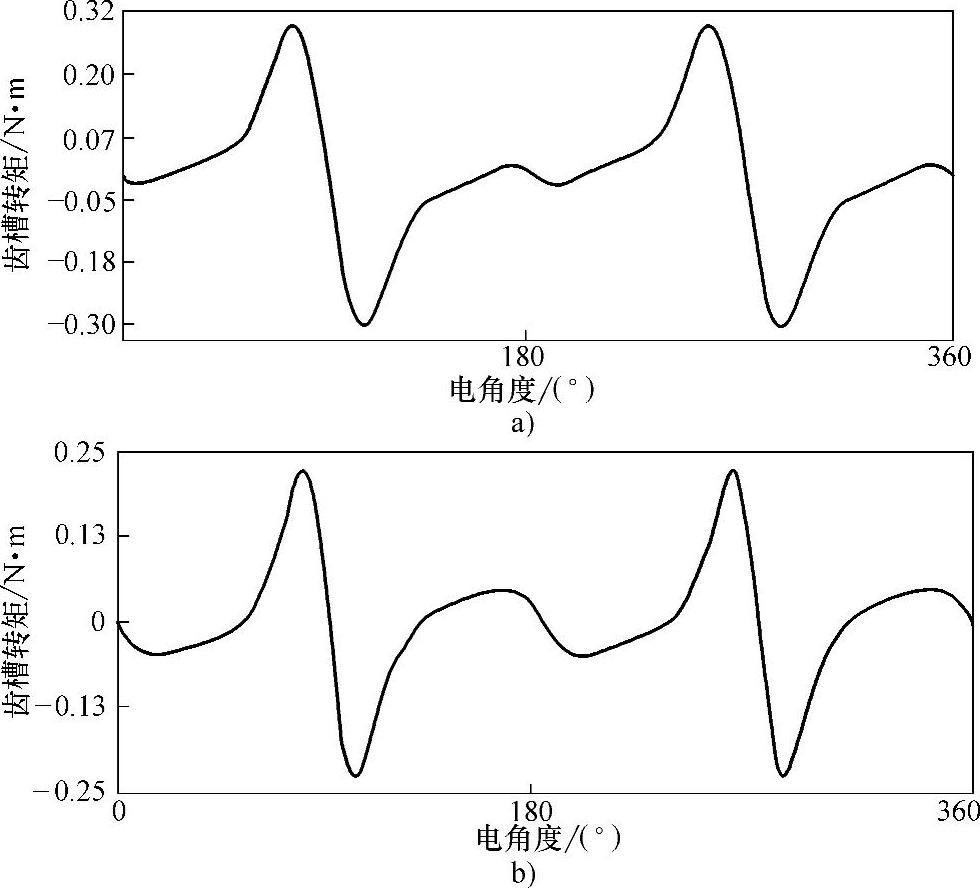
图4-50 优化前后齿槽转矩波形

a）优化前齿槽转矩 b）优化后齿槽转矩