齿槽转矩抑制技术有效应用于新能源汽车电机设计及弱磁控制

齿槽转矩（Cogging Torque）是永磁电机绕组不通电时即定子绕组激励等于零时转子的永磁体磁场与定子铁心之间相互作用产生的转矩，它会导致电机产生振动和噪声，这可通过定子斜槽、转子斜极、减少定子槽口宽度、改变极弧系数等方法来消除^[19-21]。

1）减少槽口宽度或采用磁性槽楔，以减少定子开口槽引起的气隙磁导变化。

2）采用定子斜槽，虽可有效地消除齿槽转矩谐波，但是会增大导体的占槽面积，增大电机的铜耗。

3）选择合理的极弧系数，削弱齿槽转矩。

4）选择合理的极槽配合，使一个齿距内齿槽转矩的周期数较多，能有效地削弱齿槽转矩。

为了分析简便，给出电机齿槽模型，如图4-41所示。如图4-41a所示，取轴向位置为零时（即z=0）槽1截面的中心作为气隙圆周的零位置。转子位置角α即为气隙圆周零位置（θ=0）与永磁体PM1中心的夹角。因此，图4-41a所示的转子所处位置为初始位置，即α=0。

如果电机总的斜槽倾斜角为α_s，在某一轴向位置z上槽1截面的中心相对气隙圆周零位置倾斜的角度为zα_s/L_ef，如图4-41b所示。

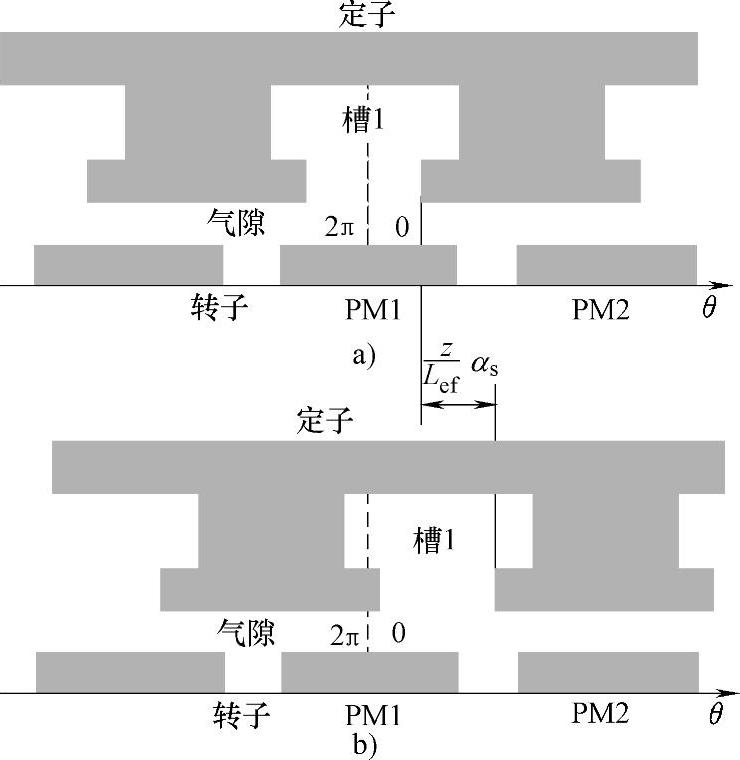
图4-41 简单的齿槽模型

齿槽转矩的一般表达式为

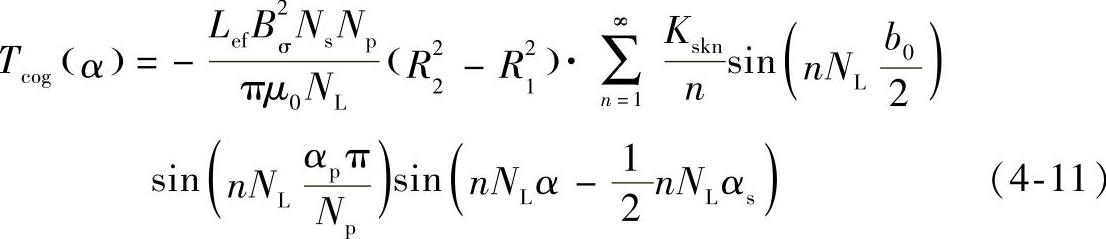
式中 _μ0——气隙相对磁导率；

R₂——气隙的外径；

R₁——气隙的内径，隙圆周的角度分布；

L_ef——电机有效轴向长度；

N_p——永磁体极数；

N_s——定子槽数；

N_L——N_p和N_s的最小公倍数，N_L=LCM（N_s，N_p）；

α——转子位置角，即气隙圆周零位置（θ=0）与永磁体PM1

中心的夹角。

在式（4-11）中，齿槽转矩中所有影响齿槽转矩的电机设计参数都能体现出来。显然，电机轴向有效长度L_ef和永磁体气隙磁通密度幅值Bσ越大，则齿槽转矩就越大。然而，在实际设计电机时，受诸多设计要求如电机的总体尺寸和输出功率的限制，电机轴向有效长度L_ef和永磁体材料的选择相对固定。因而，这里将重点分析通过对体现在式（4-11）中的槽极配合、极弧系数、斜槽等参数的优化以使得齿槽转矩最小化。

1.极弧系数的优化法

由式（4-11）可知，当极弧系数满足式（4-12）所示关系时，齿槽转矩最小。

从中可以得出，当齿槽转矩最小时α_p的值为

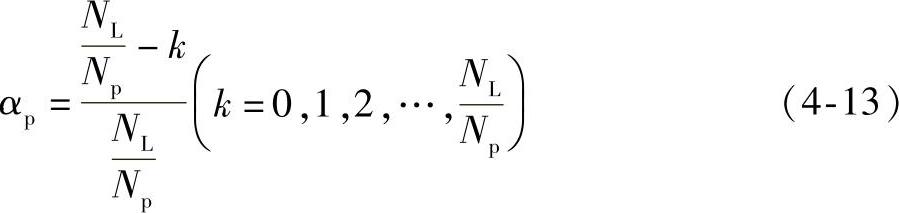
如果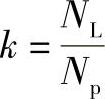，则α_p=0。但是这种情况是不存在的，因为此时将不存在永磁体。如果k=0，则α_p=1。但是考虑到极间漏磁和边界效应，这种情况也不予考虑。因此，齿槽转矩最小时优化的极弧系数α_p应为

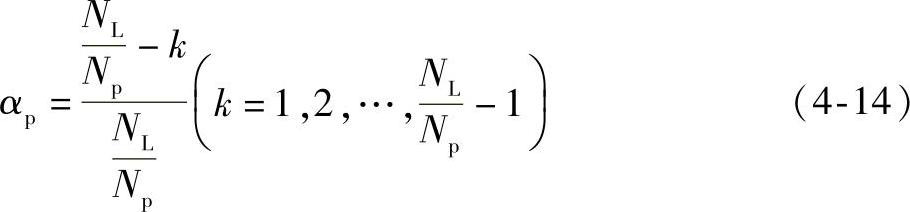
依据式（4-14），对于任何有不同槽数和极数的电机来说，都可以通过对极弧系数α_p的优化使得齿槽转矩最小化^[22]。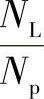的值越大，则使得齿槽转矩最小的α_p的值也就越多，此结论对表面式和内置式电机都适用^[23]。

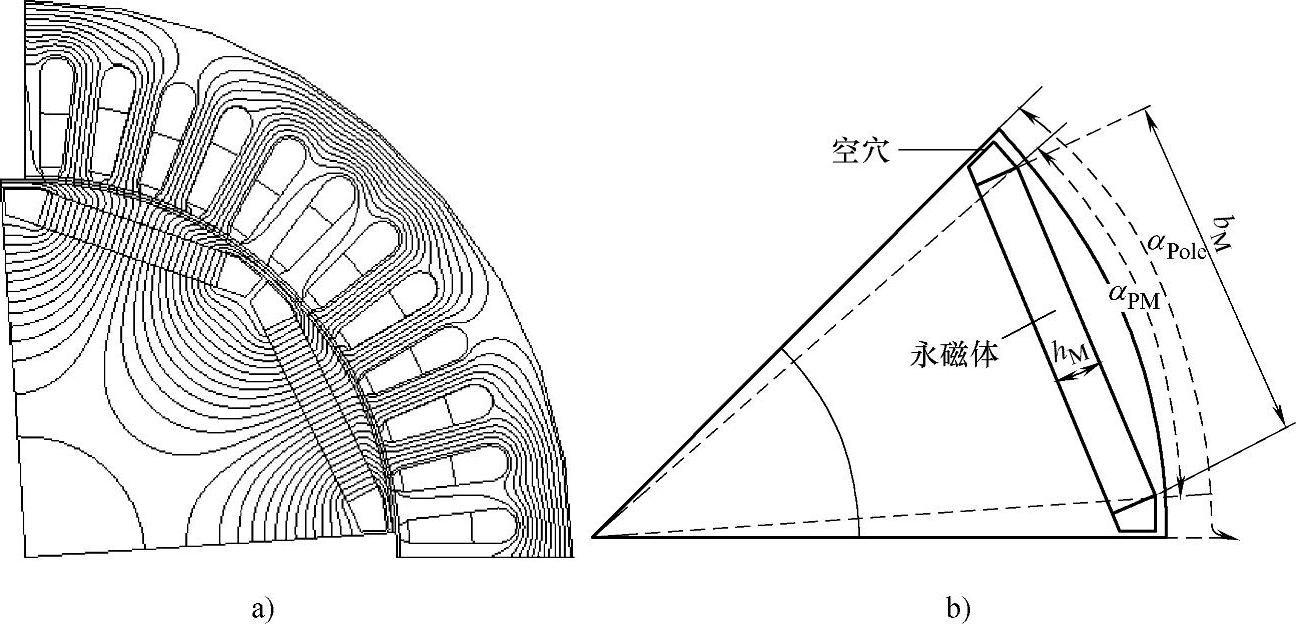
以一个传统“一”字形转子结构的内置式永磁同步电机为例，定子有48槽，转子共有8极，如图4-42a所示为其1/4有限元模型。图4-42b所示为其极弧系数。

(www.xing528.com)

图4-42 8极48槽“一”字形永磁体转子结构的内置式永磁同步电机模型

a）有限元分析模型 b）极弧系数

图4-42b中，α_Pole为一极对应的电角度，α_PM为永磁体对应电角度。极弧系数α_p为α_PM与α_Pole的比值。由式（4-14）可知，对于该8极48槽内置式永磁同步电机来说，α_p=0.83、0.67、0.50、0.33、0.17时，齿槽转矩最小。需要注意的是，如果α_p的值太小，虽然齿槽转矩减少了，但是永磁的宽度也会变得很小而不能提供足够的磁通，因此，通过优化极弧系数减少齿槽转矩时应尽量选取数值较大的α_p。对于此电机模型来说，α_p选取0.83最好，这样在减少了齿槽转矩的同时也保证了转子提供足够的磁通。

图4-43展示了通过有限元仿真得到的齿槽转矩随极弧系数α_p的关系。从中可以看出，有限元仿真结果基本上与理论分析结果一致，在α_p=0.83、0.67时齿槽转矩最小。α_p=0.83时最小齿槽转矩波形如图4-44所示。

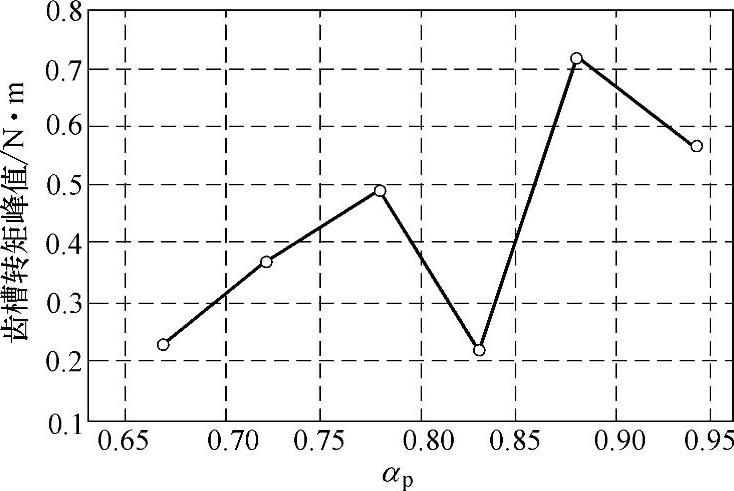
图4-43 齿槽转矩峰值与α_p的关系

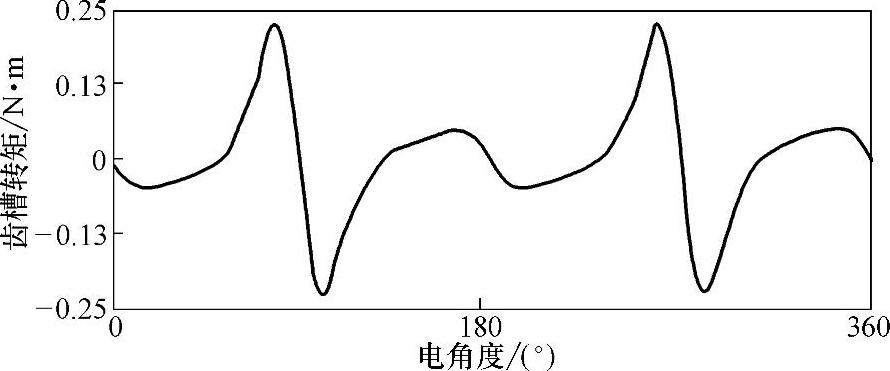
图4-44 α_p=0.83时最小齿槽转矩波形

2.定子斜槽的优化

式（4-11）中K_skn为电机的斜槽因数，即

从式（4-15）中可以看出，当N_L值很大时通过定子斜槽可以非常有效地削弱齿槽转矩。

由式（4-15）及式（4-11）可知，当斜槽倾斜角度满足式（4-16）时，齿槽转矩最小。

设α_sk为斜槽倾斜角度与槽距的比值，即

综合式（4-16）和式（4-17），式（4-16）可变形为

进而，α_sk的最优值为

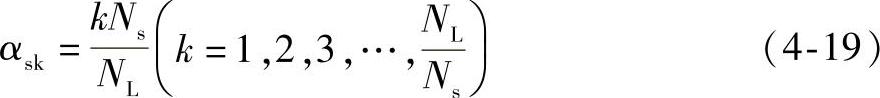
当α_sk=1，斜槽角度为一个槽距，这种斜槽方式经常被用来消除齿槽转矩。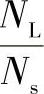的值越大，α_sk的最优值越多。式（4-19）只是列举出了α^sk小于或等于一个槽距的情况，虽然也可以采用比一个槽距大的斜槽角度，但是在实际应用中并不常用。因为这样在减少齿槽转矩的同时也会削弱反电动势峰值和输出电磁转矩平均值，同时也会加大实际制造的难度^[24]。

同样以图4-42所示传统“一”字形转子结构的内置式永磁同步电机模型为例，分别用有限元仿真求的直槽时和斜槽一个槽距时的齿槽转矩进行对比，如图4-45所示，通过斜槽一个槽距可以达到完全消除齿槽转矩的目的。

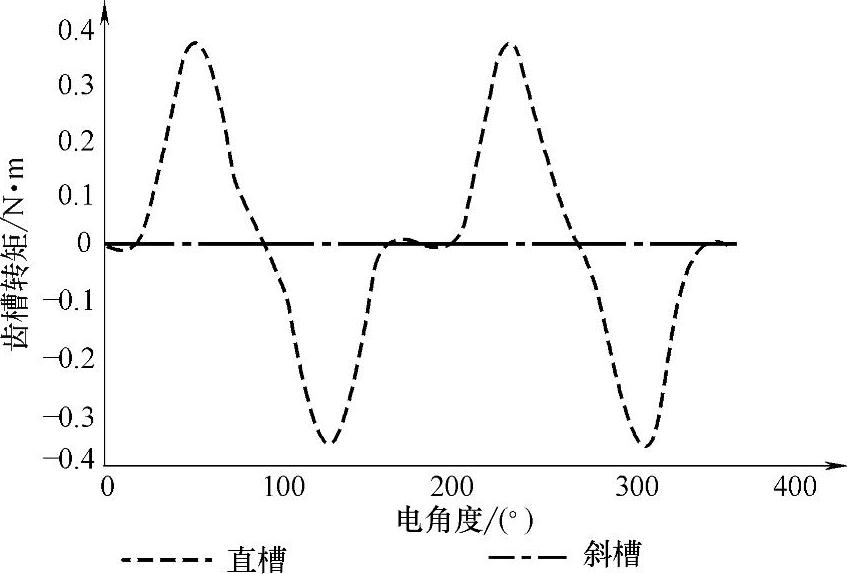
图4-45 斜槽和直槽时的齿槽转矩比较

同样的，如前所述，转子磁极斜极和定子斜槽是等效的。从图4-45中可以看出，定子槽偏斜α_s和转子磁极偏斜-α_s对电机的影响是一样的，因此如果转子磁极偏斜α_s，则齿槽转矩的表达式为

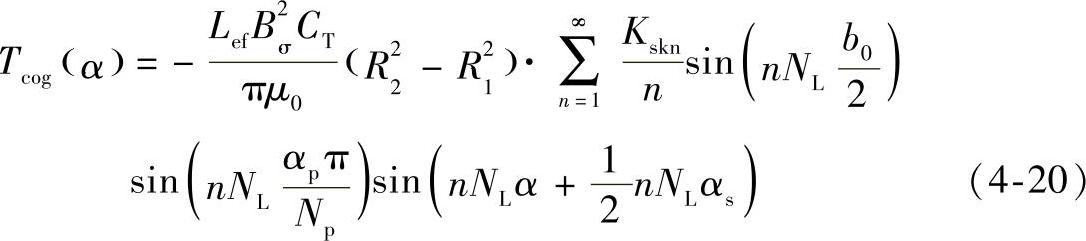
与式（4-15）相似，倾斜因数K_skn为

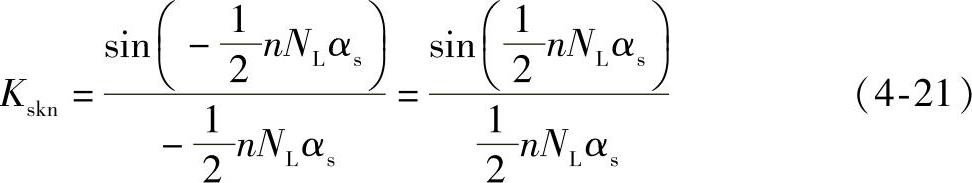
为了使得齿槽转矩最小化，转子斜极的倾斜角度需满足式（4-17），且通过转子斜极得到的α_sk的最优值与定子斜槽得到的α_sk的最优值相同。因此，定子斜槽和转子斜极在对齿槽转矩的抑制作用上是完全等效的。