设计弱磁控制的新能源汽车电机模型

2.1节对内置式永磁同步电机线性模型进行了详细的介绍，即不考虑电机饱和与铁磁材料的非线性特性。本节将介绍考虑饱和情况下的内置式永磁同步电机模型，即非线性模型。由于d轴去磁电流作用的影响，非线性饱和作用的影响主要是对q轴电感，本节也主要针对非线性模型来求解q轴电感^[8-13]。

在2.1.2节中计算q轴磁感L_qm是直接由同步电感L_ag得到的。由L_ag的计算公式我们知道同步电感与线性模型的气隙磁阻R_ag成反比。由磁阻定义，气隙磁阻可表示为

线性集总参数模型的q轴等效磁路如图2-15所示。图中，F_qs为定子q轴基波磁通势有效值，Φ_q为q轴磁通。

对于三相正弦波供电电机，设其等效匝数为N_ak_a1，则绕组F_qs计算式为

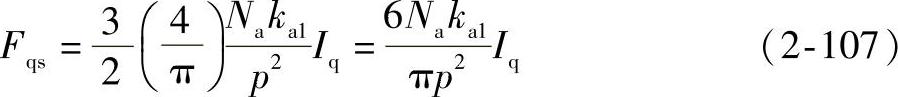
由图2-15所示等效电路可得磁通Φ_q表达式为

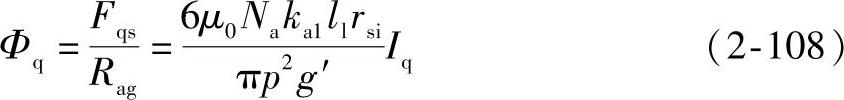
磁通乘以线圈等效匝数可得q轴磁链λ_qm表达式为

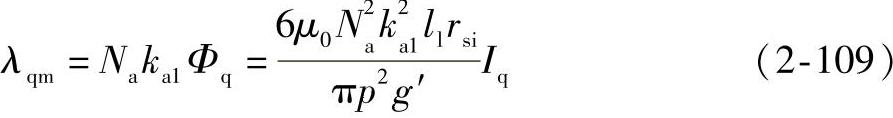
则可得q轴电感L_q计算式为

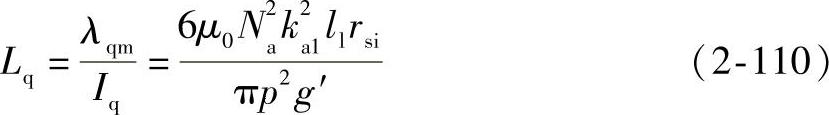
上式的计算结果和式（2-26）完全相同，由此可以看到q轴电感的分析也可以采用等效磁路的方法来分析。接下来就采用等效磁路的方法对非线性情况下q轴磁路进行建模。在大负载情况下，由于铁磁材料的渗透能力是有限的，因此一定会引起转子铁心的饱和。对于这里所设计的永磁同步电机，其可能发生饱和的分布如图2-16所示。

图2-16中永磁体将转子分为Ⅰ和Ⅱ两部分，灰色区域表示发生饱和可能性较大的区域。图中对应于q轴Ⅰ部分较容易发生饱和，而Ⅱ部分容易发生饱和的部分对应的是d轴，对应于q轴部分相对转子铁心体积较大，而且穿过对应此段气隙的q轴方向源磁通势几乎为零，因此这一部分相对不容易发生饱和。饱和情况磁阻的变化主要取决于非线性铁磁材料的磁特性。图2-17所示为该设计所采用的转子铁心材料M19_29G的B-H曲线。

图2-15 线性模型q轴等效磁路

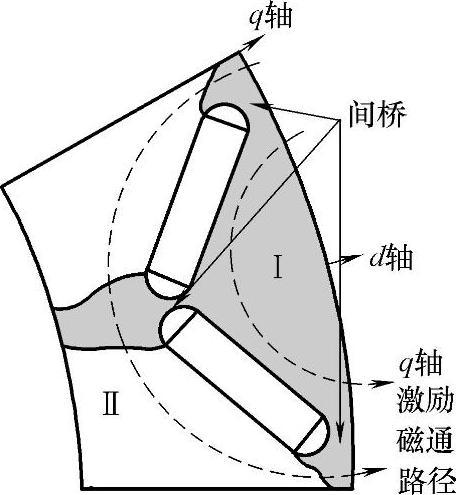
图2-16 转子一极饱和程度分布图

非线性铁磁材料特性通过符合材料B-H曲线的非线性函数表示为

则第i部分（i=1，2）在饱和情况下磁阻可表示为

式中 l_i——每部分磁阻的等效长度；

B_i——每部分磁阻的平均磁通密度；

A_i——每部分磁阻的等效截面积。

图2-18中，R_sy表示定子轭等效磁阻；R_st表示定子齿等效磁阻；R_ry表示转子侧等效磁阻；Ф_q为沿q轴方向等效磁通。

图2-18所示为一最简单考虑q轴磁路饱和情况的q轴等效磁路，根据定转子磁路饱和程度不同分别计算磁阻，但是对于定子侧看作均一体，同样转子侧也看作均一体。

但是对于转子来说其磁路并非保持均一，如该设计中永磁体内侧和永磁体外侧其磁路的饱和程度就不同，因此图2-18所示等效电路就不能详细地反映定转子上等效电路结构。为了更精确地计算转子侧磁阻，采用图2-19所示等效电路来描绘q轴等效磁路。

图2-19中，R_ryn（n=1，2，…，k）为转子铁心不同部分对应的等效磁阻，其对应的转子平均磁通势近似计算式为

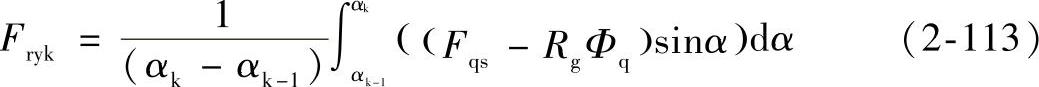
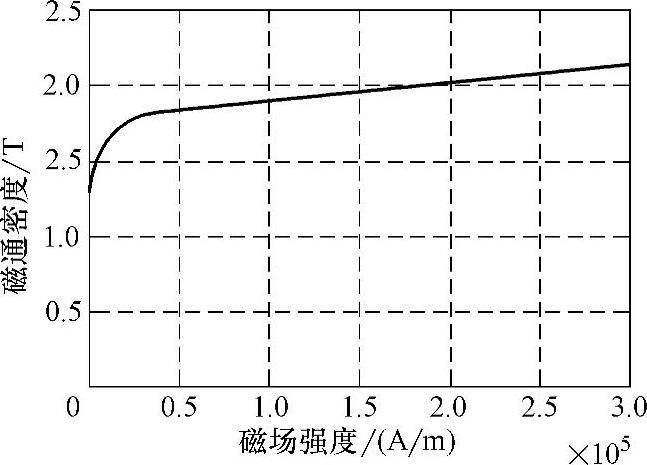
图2-17 铁心材料M19_29G的B-H曲线(www.xing528.com)

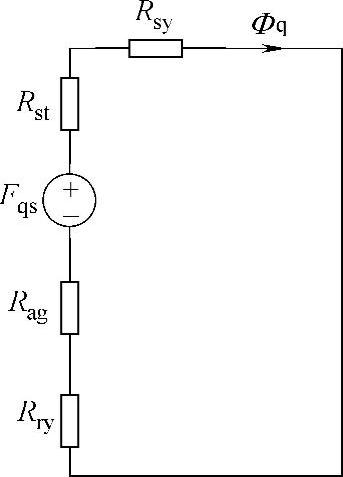
图2-18 简单地考虑饱和的q轴等效磁路

图2-19所示的等效磁路不但考虑了定子齿和轭部分磁路饱和程度不同的情况，还考虑了转子结构引起的转子不同部分磁路饱和程度不同的情况，因此其分析结果较图2-18更精确，这对于内置式，尤其是非传统内置式或多层内置式结构来说意义更大。图2-20所示为更复杂的一种等效形式。

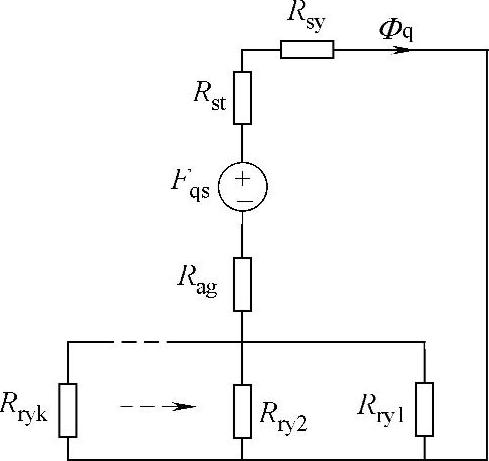
图2-19 较精确考虑饱和的q轴等效磁路

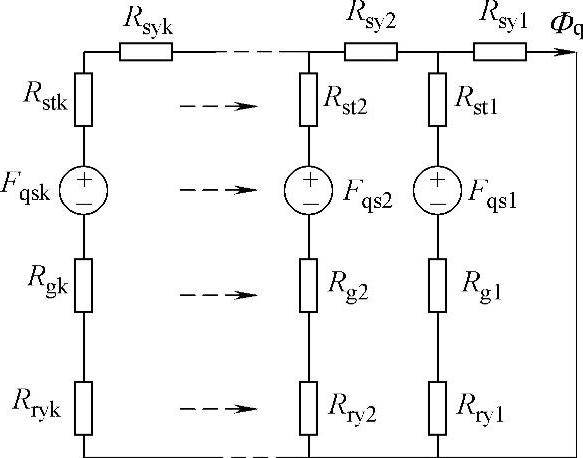
图2-20 精确地考虑饱和的q轴等效磁路

这种特效形式不但考虑了转子结构不同部分的复杂情况，而且还考虑了由于转子造成的对定子侧的影响，将定子侧也分成若干部分，分别进行等效，其电路结构会变得更加复杂，但是由于其更全面地考虑了各方面的影响，分析结果也更加精确。

为了更为精确地进行估算，这里采用图2-20所示的等效磁路对q轴电感进行估算。针对该设计电机，由图2-20可得精确考虑饱和情况的q轴磁路等效模型如图2-21所示。

等效模型中各个等效磁阻均为非线性磁阻，其大小采用式（2-112）进行计算。各等效磁阻的长度采用等效长度表示，其大小如图2-22所示。对应第k层（离转子内边界最近的为第一层）定子齿部分等效截面积为

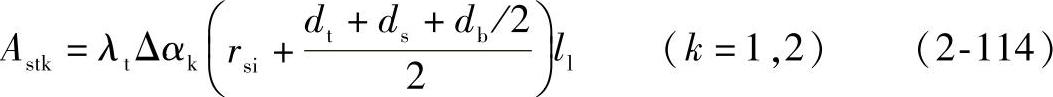
式中 λ_t——在α_k-1到α_k之间这段气隙的磁链值。

对应第k层部分定子轭部分平均截面积可表示为

A_syk=A_sy=d_bl_l （k=1，2） （2-115）

则第k层对应气隙磁阻可表示为

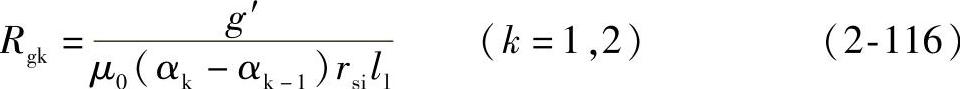
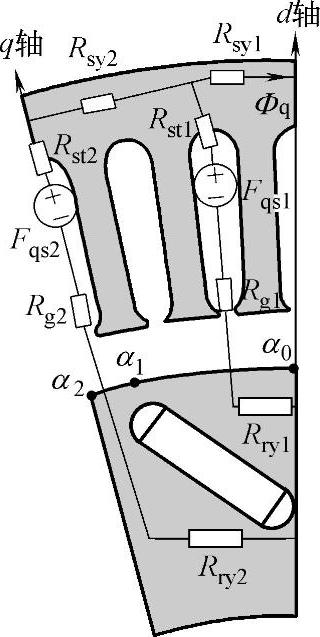
图2-21 精确地考虑饱和的q轴等效磁路示意图

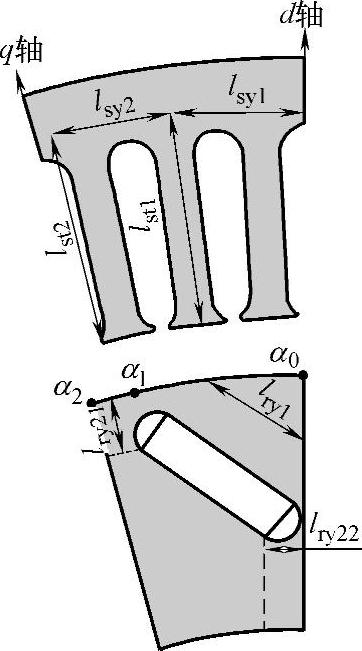
图2-22 等效磁阻等效长度示意图

对应第k层的定子磁通势激励为

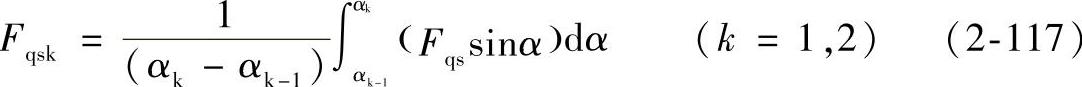
转子永磁体内侧，即图2-16中所示Ⅰ部分的转子铁心，其等效磁阻截面积可近似为

转子永磁体外侧，即图2-16中所示Ⅱ部分的转子铁心，其等效长度由两部分构成，对应于l_ry21和l_ry22的等效截面积分别近似为

由上述的分析，考虑饱和情况的q轴等效磁路中各元件大小均可确定，则通过式（2-107）所示激励源迭代求解，即可求得每层对应的q轴磁通势分量，进一步可得到q轴磁通。则考虑饱和的q轴磁链和磁感分别为

则总的q轴电感可表示为

L_qs=L_qms+L_l （2-122）

用上式所示q轴电感取代线性模型中的q轴电感即得到了考虑饱和的电机模型。