这里主要从四个方面对电机损耗进行分析计算，即定子电枢损耗、定子铁心损耗、齿槽谐波损耗和机械损耗。
三相内置式永磁同步电机定子电枢损耗表达式为
Pa=3RaI2a （2-71）
Ra——相电阻。
如前面章节所介绍的，相电阻大小与电机定子轴向长度和线圈类型有关。因为线圈都是闭合的，因此槽与槽之间的连接部分会高出定子。一般比较合理的估算方式是，认为端部高度Lel为单股线圈宽度wa的3倍，即
Le1=3wa （2-72）
则电机轴向总长度可表示为
lout=ll+2le1 （2-73）我们近似认为线圈端部跨线与定子圆周平行，则线圈端部长度可表示为
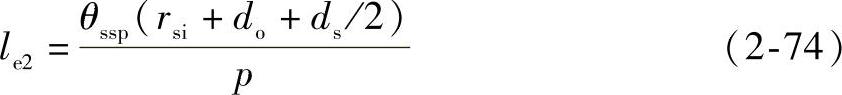
则由上述可得单相线圈总长度为
la=Na（2ll+4le1+2le2） （2-75）
绕组横截面积Aa由所选用的导线规格、所选择槽型，以及特定的槽满率决定，其大小可表示为
式中 λa——槽满率。
当忽略趋肤效应的影响时，设定绕组电导率为σa，则定子线圈相电阻可表示为
定子铁心损耗主要由磁滞损耗和涡流损耗两部分组成。这些损耗都取决于定子、转子铁心材料和定子铁心叠片厚度。但是对于某一特定的材料，其磁特性随制造批次不同都会产生微小的变化，而且冲压、激光切割也会对材料的磁特性产生影响。因此，即使相同设计类型和材料，也无法采用此种材料的一般磁特性曲线对定子铁心的损耗进行较为精确的量化处理。在该设计中，引入了一份有关电气应用钢铁制造的报告中关于材料典型特性的规定方式，对定子铁心损耗进行合理的考虑[5]。在报告中，它把定子铁心损耗表示为与磁感强度和激励源角频率相关的双指数形式，即
式中 Pci——第i段铁心损耗；
mi——第i段铁心质量；
Bi——通过该段的平均磁通密度；
ωr——转子电角速度。
式中的其他参数取决于材料。以该设计中所采用的材料M19_29G为例，相关参数如表2-1所示[6]。
表2-1 M19_29G铁心损耗模型参数
这些参数的测定都认为磁材料是线性非饱和的，忽略谐波频率损耗，并且认为气隙磁场是正弦的。
一般认为估算量是比较保守的，即估算结果有一定精度范围。在低频额定运行情况下，线性模型估算的定子铁心中的平均磁通密度Bi可能会远远高于实际值，然而在低频率段时，平均磁通密度对于定子铁心的损耗影响是微乎其微的，因此对损耗的计算影响不是很大。但在高速弱磁运行区域，由于弱磁的作用，尽管激励频率增加，磁通密度反而减少，因此估算得到的值要小于实际值。
定子铁心磁通密度可以分为两部分即定子齿和轭分别进行分析，对于带负载运行电机，其气隙磁通密度Bag与气隙电压Uag有关，其大小可表示为
由气隙磁通密度可得，定子铁心齿上的磁通密度为
Bt=（1-λssp）Bag （2-80）
假设所有的气隙磁通全部都通过齿，即不考虑漏磁，则轭部分的磁通密度为
一般轭部磁路饱和是非线性的，忽略饱和则齿部分的定子铁心损耗Pt和轭部分的定子铁心损耗Pdb分别为
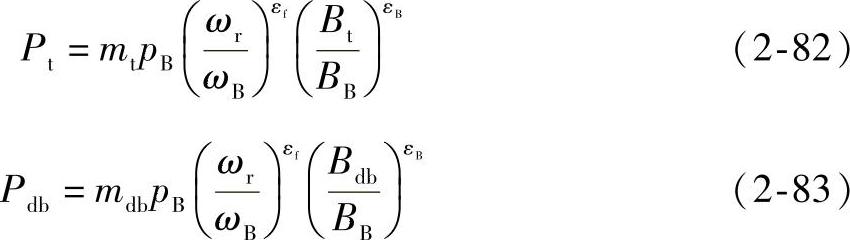(www.xing528.com)
式中 mt——齿部分定子铁心质量；
mdb——轭部分定子铁心质量。
综上所述可得定子铁心总损耗为
Pc=Pdb+Pt （2-84）
最后计算槽感应谐波铁损，这主要是由于定子槽采用开口槽所引起的。由于定子槽为开口槽，造成气隙的不均匀从而引起气隙磁通谐波，它们通过气隙作用引起转子表面涡流从而引起转子表面磁场改变，产生槽感应谐波损耗。这里通过定子槽模型对谐波幅值进行估算，其渗透性通过铁心表面电导率σc进行衡量。
半开口槽的开口角度计算式为
槽谐波磁通密度的幅值Bh和角频率ωh分别为
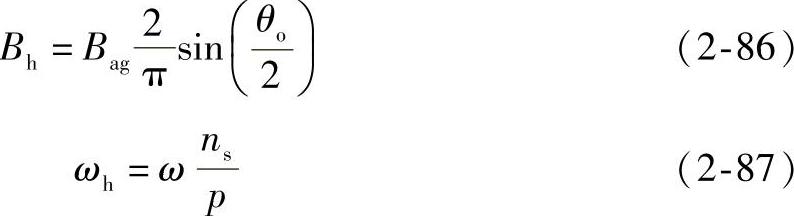
式中 ω——转子机械角频率。
则其在转子表面产生的电动势Ez和电流Iz为
式中 Zs——转子表面等效阻抗，大小为
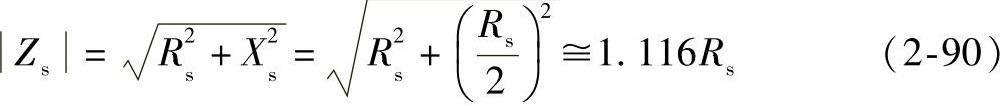
式中 Rs——转子表面电阻，其大小为
式中 δc——渗透深度，其大小为
式中 B0——铁心饱和度为75%时的磁通密度。将式（2-88）、式（2-89）、式（2-90）和式（2-91）带入到式（2-92）中，对其化简则有
则槽谐波铁损为
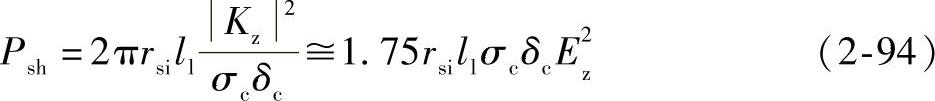
考虑电机的铁心损耗情况下，永磁同步电机d轴和q轴等效电路如图2-13所示。
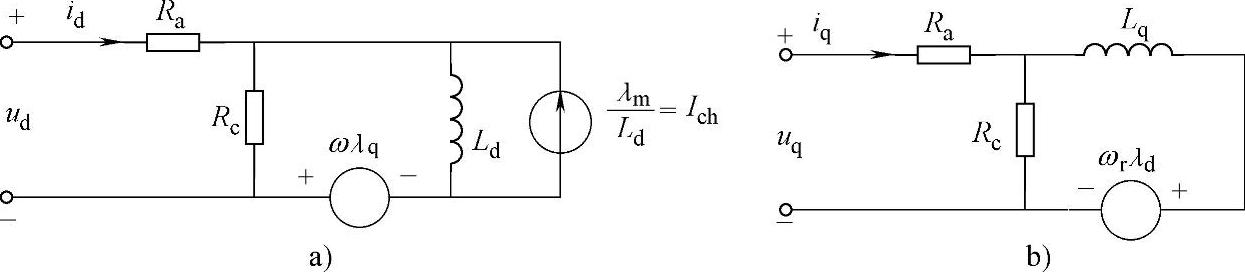
图2-13 考虑电机铁心损耗的永磁同步电机d轴和q轴等效电路
a）d轴等效电路 b）q轴等效电路
图2-13中，Rc表示铁心损耗等效阻抗。
机械损耗主要由摩擦损耗和风损两部分组成。摩擦损耗和风损没有比较精确的计算表达式。在一般的工程中一些工程师在设计时，采用额定功率的0.5%～1.5%来考虑这部分损耗。这里为了更为精确地考虑这部分损耗，引入了Gieras给出的经验计算公式。摩擦损耗Pfr和风损Pwind估算式分别为
式中 Kfb——摩阻系数；
mr——转子质量；
nr——电机当前转速。
则机械损耗为
Pm=Pfr+Pwind （2-97）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
