内置式永磁同步电机的磁路结构是不对称的,如图2-4所示。
从图2-4中可以看出,d轴磁链穿过2个永磁体和2个气隙,q轴只通过了铁心和2个气隙,没有通过永磁体,因此q轴磁导大于d轴磁导,故交轴电感Lq大于直轴电感Ld,即Lq与Ld的比值大于1,该比值为永磁同步电机的凸极率。其方程为
ξ=Lq/Ld (2-12)
电感是衡量线圈产生电磁感应能力的物理量,是单位电流所产生的磁链。如果通过线圈的磁链用λ表示,电流用i表示,则电感L可表示为

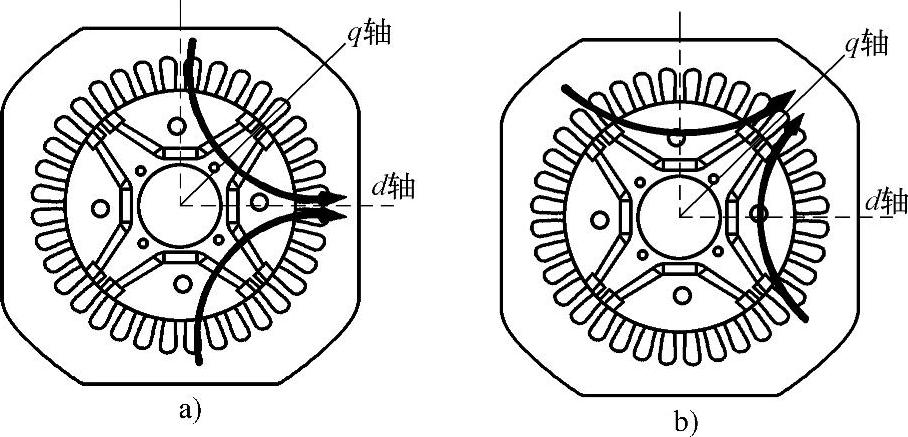
图2-4 内置式永磁同步电机d轴和q轴磁路示意图
a)d轴磁路 b)q轴磁路
也可表示为
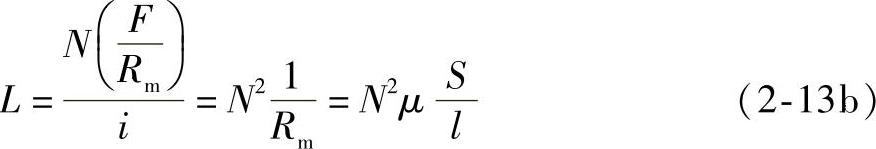
式中 N——导体的匝数;
μ——磁导率;
F——磁通势;
S——自感磁通所经磁路的截面积;
Rm——磁阻;
l——自感磁通所经磁路的平均长度。
当磁路为非铁磁材料,μ为常数,近似等于真空磁导率μ0,故L为常数,有B=μ0H。若磁路为铁磁材料,由于铁的磁导率μFe≥μ0,且随铁磁材料的饱和下降。在工程中,为了方便,铁磁材料的磁导率一般采用相对磁导率表示,其大小为

内置式永磁同步电机一个极的横截面图和定子槽型尺寸图分别如图2-5和图2-6所示。假设三相内置式永磁同步电机每极每相槽数为ma,极对数为p,则电机每极槽数nsp(极距槽数)为
nsp=3ma (2-15)
齿距角度θt为

定子总槽数ns为
ns=2pnsp (2-17)
设定子节距槽数为nssp,则短距比λssp为

则可得单个线圈实际跨过的机械角度θssp为
θssp=πλssp (2-19)
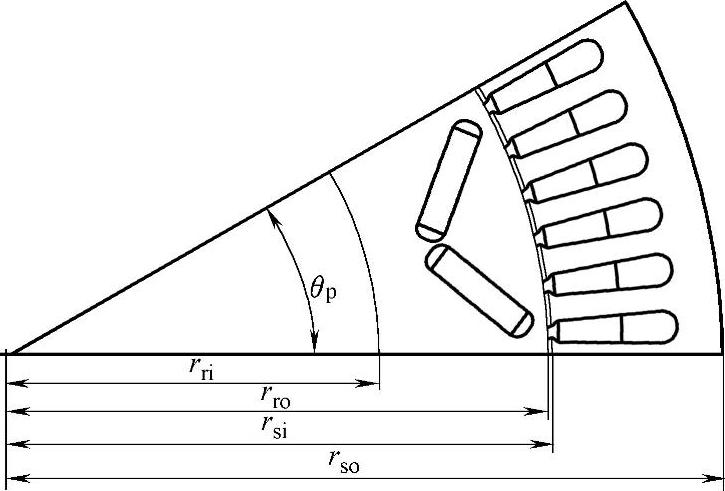
图2-5 一极定转子剖面图
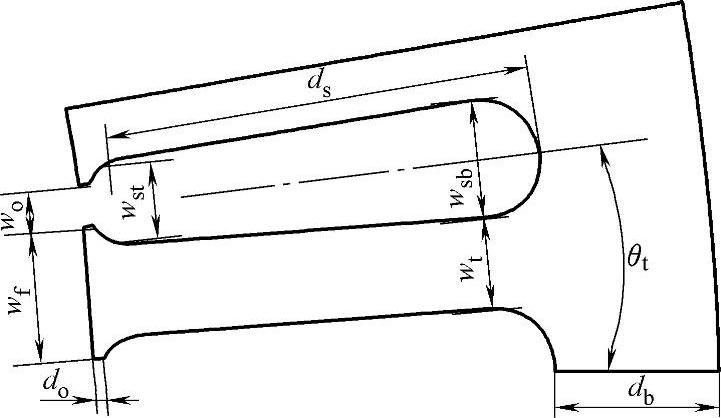
图2-6 定子槽型尺寸图
电机极距因数kbn、节距因数kpn、斜槽因数ksn和绕组因数kan分别为
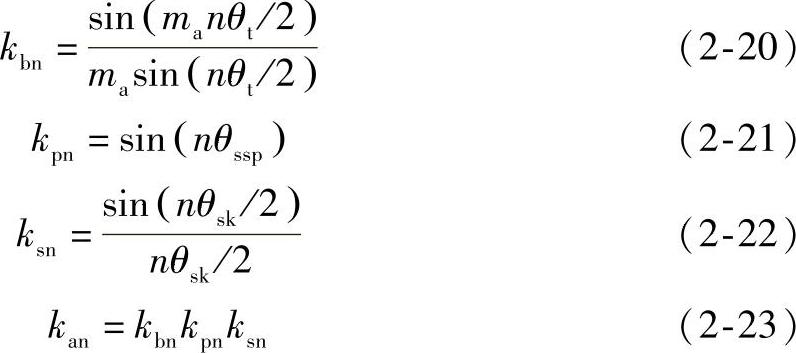
式中 θsk——斜槽角度;
n——谐波次数。
由图2-5可知气隙长度g=rsi-rro,由于这里设计电机采用的是开口槽,而齿槽效应的影响使得实际的气隙并非均匀,根据图2-6所示的定子槽型及其尺寸可得等效气隙长度g′为

式中 kcs——卡特系数,其方程为

则由式(2-13b)电感定义可得三相内置式永磁同步电机一相的气隙同步电感(此值只包括了基波分量,没有考虑谐波的影响)为

式中 μ0——真空磁导率;
rsi——定子内径;
p——极对数;
Na——相线圈匝数。
磁通势中一般都含有谐波,主要是5次和7次谐波,也包含一些高次谐波。这些谐波分量都不参与产生转矩,而是贡献为气隙漏感。第n次谐波引起的漏感值为
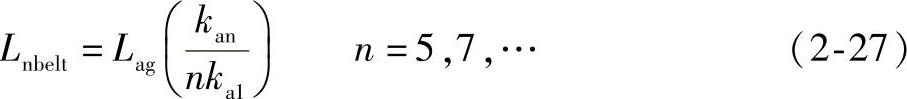
在这里设计的电机中定子漏感主要由两部分组成,一部分是由于开口槽面引起的,称为“zig-zag”漏感;另一部分是由槽本身引起的,称为槽漏感。“zig-zag”漏感是在每极每相槽数大于1的情况下,没有经过定子绕组或只经过一相的部分绕组所引起的。根据磁力线方向不同,引起的谐波次数分别为

式(2-28)所示谐波次数下“zig”极距因数kbfz、节距因数kpfz、斜槽因数ksfz和绕组因数kafz以及“zag”极距因数kbbz、节距因数kpbz、斜槽因数ksbz和绕组因数kabz分别为

则可得“zig”漏感Lfzig和“zag”漏感Lbzag分别为
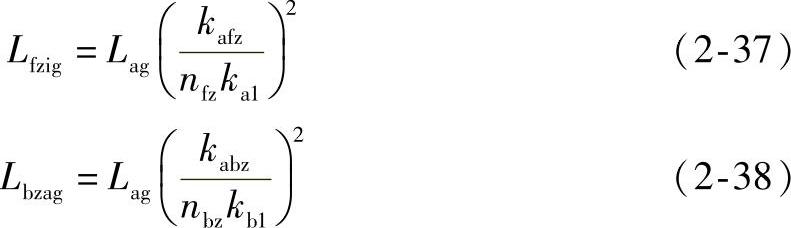
定子槽漏感计算,这里引入了Lipo提出的计算模型[3]。首先定义定子槽平均宽度wsa和短距因数kssp。由图2-6所示尺寸可得定子槽平均宽度表达式为
 (https://www.xing528.com)
(https://www.xing528.com)
短距因数计算式为

则漏磁路径的磁导率可表示为
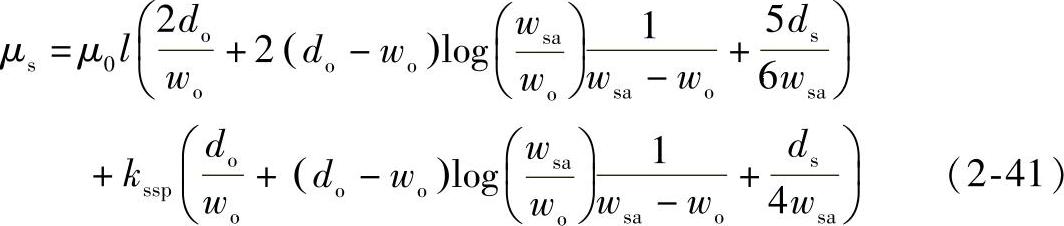
根据引入的计算模型[3]可得定子槽漏感方程为

端部漏感方程为
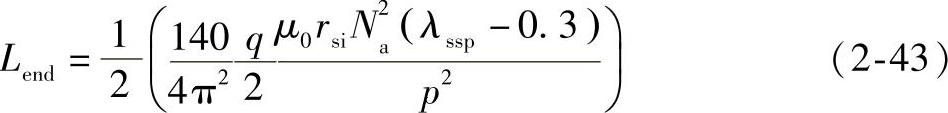
综上所述,可以得到总漏感表达式为
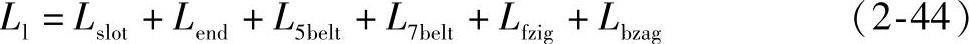
则内置式永磁同步电机总的同步电感Ls可表示为
Ls=Lag+Ll (2-45)
如2.1.1节所述,为了方便性能分析一般采用与转子同步旋转的dq参考坐标系进行分析。因此分析中采用dq坐标系的等效电感,本小节将对等效的d轴电感Ld和q轴电感Lq进行分析计算。由图2-4所示的内置式永磁同步电机d轴和q轴磁路可以看出,q轴磁路全部穿过转子铁心,其电感参数的计算采用的是气隙磁阻模型,而d轴磁路必须通过永磁体,其参数的计算这里引入了Fratta和Vagati等所建立的模型进行计算[4]。d轴电感和q轴电感可分别分解为磁感和漏感两部分,即
Lq=Lqm+Ll (2-46)
Ld=Ldm+Ll (2-47)
对于旋转永磁同步电机,气隙磁链几乎全部通过铁心和转子气隙形成闭合回路,因此当不考虑磁路饱和时,即认为任何时刻磁路是线性变化的,由q轴电感磁路分析可近似地将同步电感看作q轴磁感,即有
Lqm=Lag (2-48)
内置式永磁同步电机转子表面是气隙均匀的,在不考虑饱和的情况下,漏感将完全取决于定子和绕组设计,因此q轴漏感等于同步气隙漏感,即有
Lq=Ls (2-49)
由磁通路径的分析可知,d轴等效电感只有磁感部分[3]。在此引用参考文献[4]的分析方法,将磁感分成两部分进行分析,即
Ldm=Ldt+Ldc (2-50)
式中,Ldt和Ldc通过等效磁路分析的方法计算。首先,做如下假设:
1)铁心具有无限渗透能力,即在任何情况下都认为磁路是不饱和的;
2)磁矫顽力是常数;
3)间桥处转子铁心深度饱和。
则可得k层永磁体情况下磁路的等效模型如图2-7所示。
图2-7中,fdsn(n=1,2,…,k)表示每层永磁体对应的定子磁通势源;fdrn(n=1,2,…,k)表示每层永磁体对应的转子表面磁通势源;rgn(n=1,2,…,k)表示每层永磁体对应气隙段的气隙等效磁阻;rmn(n=1,2,…,k)表示每层永磁体自身等效磁阻;Фd为沿d轴方向等效磁通。
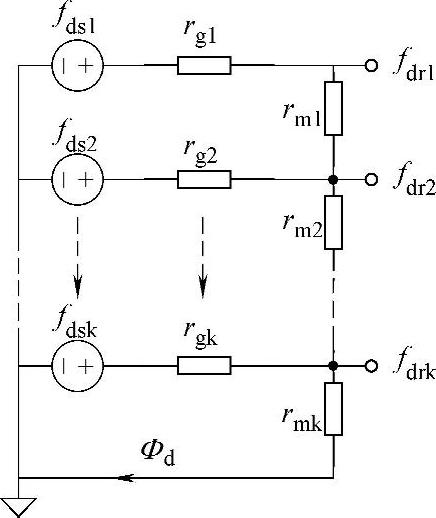
图2-7 k层永磁体内置式永磁同步电机等效d轴电感电路

图2-8 单层永磁体内置式永磁同步电机等效d轴电感电路
图2-8所示为单层永磁体内置式永磁同步电机等效d轴电感电路,其中αk为等效磁路中各段覆盖的角度分界点,这样将气隙分成相应的k段。各段所覆盖的面积用Δαk表示,其大小为
Δαk=αk-αk-1 (2-51)
定子气隙面积Ar为
Ar=2πrsill (2-52)
式中 ll——电机有效长度,即电机的深度。定子齿距截面积As为

永磁体截面积Amk为
Amk=lmkll (2-54)
式中 lmk——第k层永磁体所覆盖转子表面的等效长度。
则图2-7和图2-8中所示的各磁阻阻值为

式中 dmk——第k层永磁体的厚度。
第k层定子磁通势源大小为

图2-7中所示内置式永磁同步电机第k层对应的转子表面磁通势为
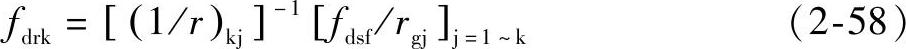
其中:

针对这里设计的电机,上述激励源与电阻模型中取k=1即可。
由上述磁路模型分析结果和参考文献[4]可得d轴电感的Ldt分量和Ldc分量分别与q轴磁感比值计算公式为
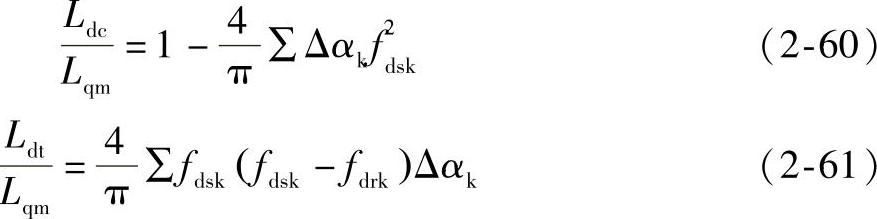
则d轴磁感,即d轴总电感为
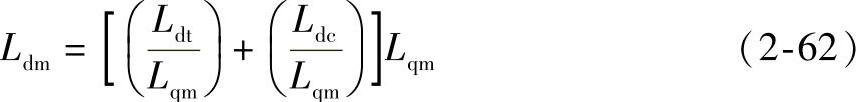
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




