新能源汽车电机设计及弱磁控制方案

三相永磁同步电机是一个多变量、非线性、强耦合系统，为了便于分析，需做如下假设：

1）定子绕组三相对称并且完全相同，各相绕组轴线相差120°。

2）忽略磁路饱和、磁滞和涡流的影响，磁路是线性的，可以用叠加原理进行分析，转子上没有阻尼绕组。

3）当定子绕组电流为三相对称正弦波电流时，气隙空间中只产生正弦波分布的磁通势，无高次谐波分布。

4）永磁体在气隙空间中产生的磁通势为正弦波分布，无高次谐波，也就是电机定子在空载时电动势为正弦波。

下面介绍三相静止坐标系下的电机模型和同步旋转的dq坐标系下内置式永磁电机模型。

1.三相静止坐标系下的电机模型

基于上述假设，可以得到在三相静止ABC坐标系中，定子电压方程为

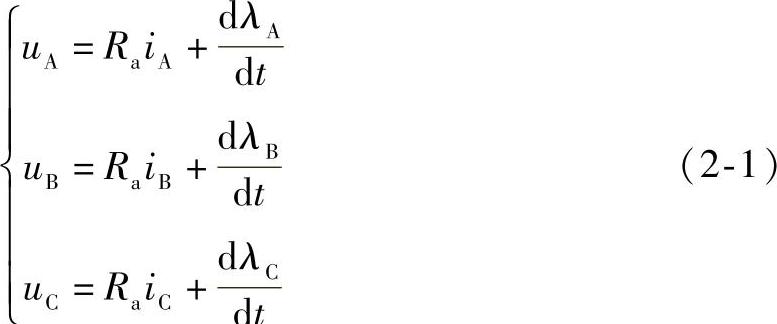
式中 u_A，u_B，u_C——三相绕组相电压；

R_a——每相绕组电阻；

i_A，i_B，i_C——三相绕组相电流；

λ_A，λ_B，λ_C——三相绕组的磁链。

定子每相绕组的磁链不仅与三相绕组电流有关，而且与转子永磁磁极的励磁磁场和转子的位置角有关，磁链方程为

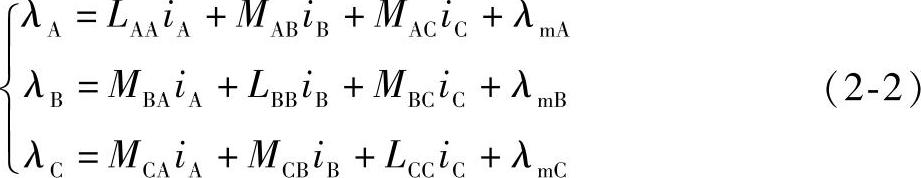
式中 L_AA，L_BB，L_CC——每相绕组自感；

M_AB=M_BA，M_BC=M_CB，M_CA=M_AC——两相绕组互感；

λ_mA，λ_mB，λ_mC——三相绕组的转子每极永磁磁链，其表达式为

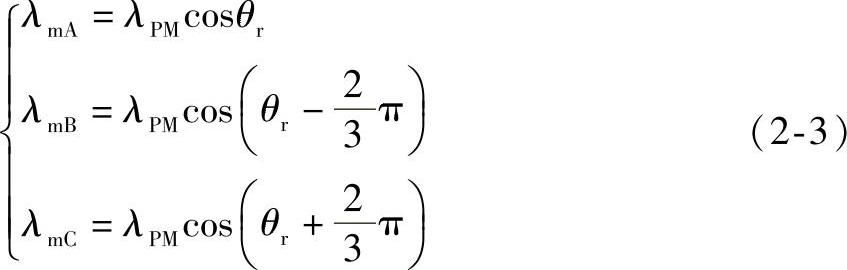
式中 λ_PM——永磁体磁链幅值；

θ_r——转子位置电角度，θ_r=ω_rt+θ₀；

θ₀——初始位置角；

ω_r——转子旋转电角速度；

t——时间。

电压、磁链均为时变量，即随角度的改变而改变。为了分析方便，可通过坐标变换将三相静止坐标系下的电机变量转化为转子随转子同步旋转的dq坐标系方程。

2.同步旋转的dq坐标系下内置式永磁电机模型

图2-1给出了永磁同步电机定子三相静止ABC坐标系、定子静止两相静止αβ坐标系和转子同步旋转dq坐标系的关系。图中，i_s为电机定子电流合成矢量，i_d和i_q分别表示d轴和q轴等效电流。定子两相静止坐标系中定义α轴与定子三相静止坐标系中A相轴线重合，超前α轴线90°电角度的位置定义为β轴。

转子同步旋转坐标系dq是将同步电机转子磁极产生磁场的N极中心轴线作为直轴即d轴，而超前直轴90°电角度的位置定义为交轴即q轴。在dq轴坐标系下，坐标轴和磁链都是以转子同步角速度ω_r旋转，电机数学模型中电压、等效永磁体磁链等参数量将转化为非时变量参数，所有电流量、电压量和磁链量均表示成空间矢量并分解成dq轴分量^[1]。

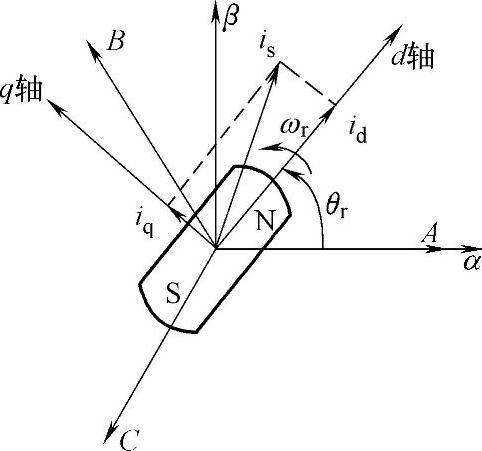
图2-1 同步旋转dq坐标与静止ABC坐标关系图

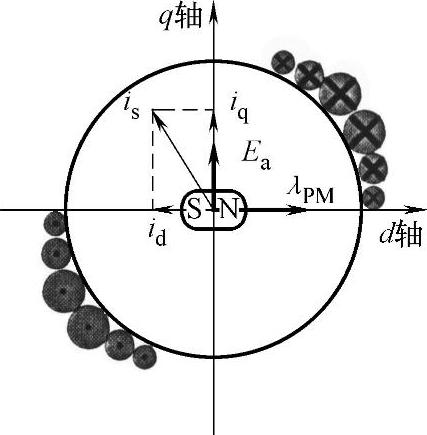
图2-2 dq轴电机模型电流矢量平面图(www.xing528.com)

图2-2所示为dq坐标系下永磁同步电机数学模型简图。在图2-2中，E_a为反电动势，其方向与q轴方向一致；λ_PM为永磁体磁链，其方向与d轴方向一致，电流矢量方向代表定子旋转磁通势的方向，其大小正比于定子电流大小。

根据坐标系关系对ABC三相静止坐标系下模型进行Clarke变换和Park变换便可得到永磁同步电机在转子同步旋转坐标系下的方程，变换矩阵为

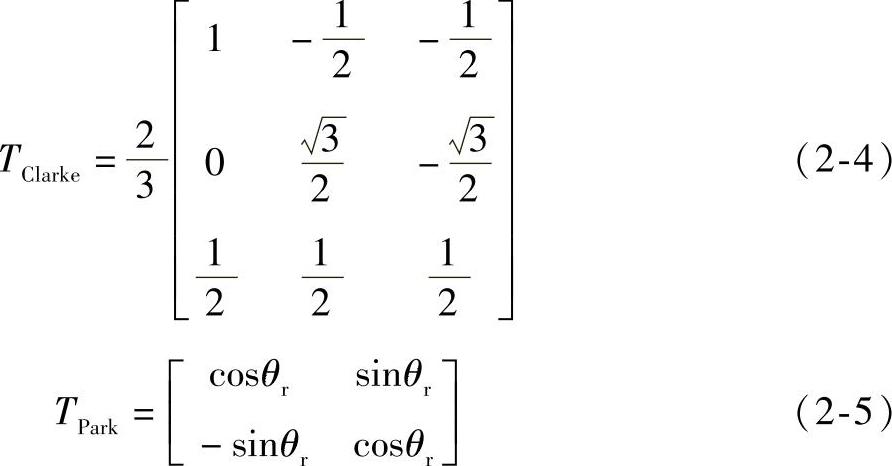
经Clarke变换和Park变换后dq坐标系下磁链方程为

式中 i_d和i_q——d轴和q轴等效电流；

L_d和L_q——d轴和q轴等效电感。

同理可得dq坐标系下电压方程为

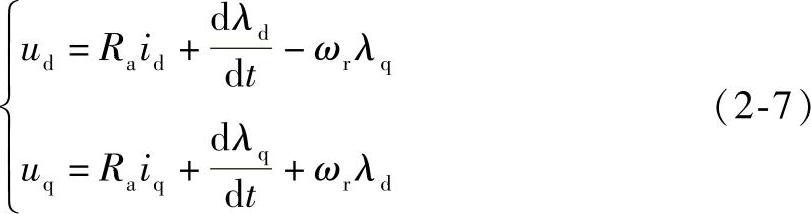
式中 u_d和u_q——d轴和q轴等效电压；

ω_r——转子的同步旋转电角速度；

λ_d和λ_q——d轴和q轴等效磁链。

由电压方程式（2-7）可以看到，dq坐标系下模型既可用于分析永磁同步电机的瞬态性能，也可以用于分析电机的稳态运行性能。由式（2-6）和式（2-7）可得d轴和q轴等效电压方程式为

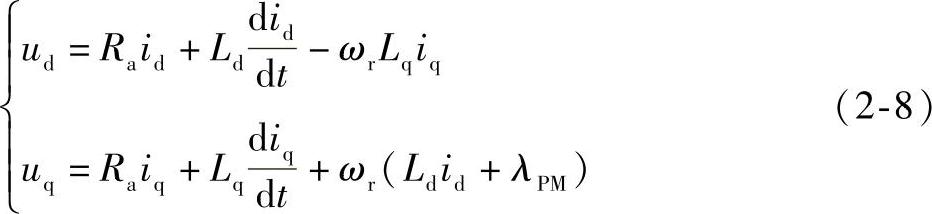
由式（2-6）和式（2-7）可得内置式永磁同步电机d轴和q轴等效电路，如图2-3所示。

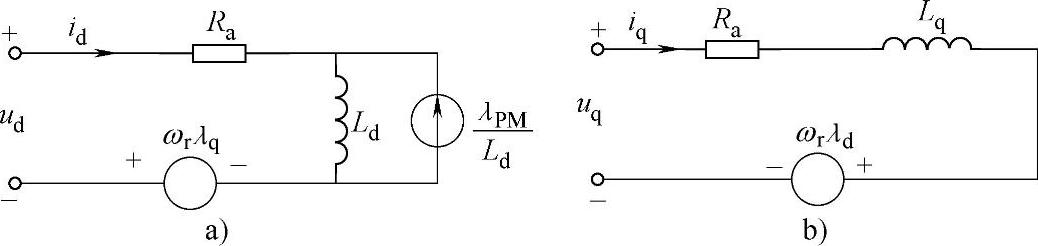
图2-3 永磁同步电机的d轴和q轴等效电路

a）d轴等效电路 b）q轴等效电路

采用保持幅值不变的3/2变换原则，由上述d轴和q轴等效电压方程（忽略定子电枢电阻压降）及d轴和q轴等效电流可得永磁同步电机功率方程为

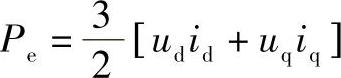
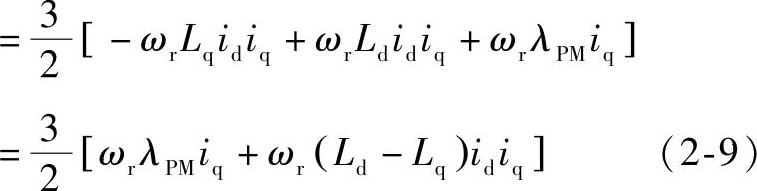
电磁功率与电磁转矩关系式为

P_e=T_eΩ （2-10）

式中 Ω——电机转子旋转机械角速度。

其中

ω_r=pΩ

电磁功率除以机械角速度Ω，可得永磁同步电机旋转dq坐标系下的电磁转矩方程为

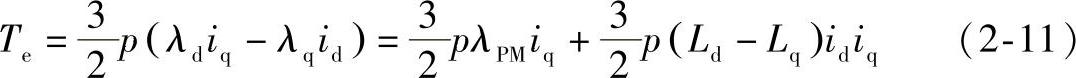
式中 p——极对数。

从式（2-11）可以看出，电磁转矩由两部分组成，一部分是永磁体产生的转矩，即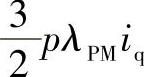，无论表面式永磁同步电机还是内置式永磁同步电机均有；另一部分是磁阻转矩，即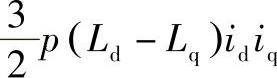，该转矩的产生是因为内置式永磁同步电机的交轴电感L_q大于直轴电感L_d。磁阻转矩的存在，不但有效地提高了电机的功率密度和转矩输出能力，而且使电机易于弱磁调速，扩大了电机恒功率运行的范围^[2]。