车辆、航海、航空、航天运载工具电力系统中前级二极管整流

假设图13-4中的整流器触发角是零（α=0）。图13-5给出了前级二极管整流器的交流恒功率负载的电压和电流波形。变换器是连续导通模式。恒功率负载的电压假设是正弦形的。如果忽略谐波，只考虑电流的基波分量。负载电压和电流可表示为：

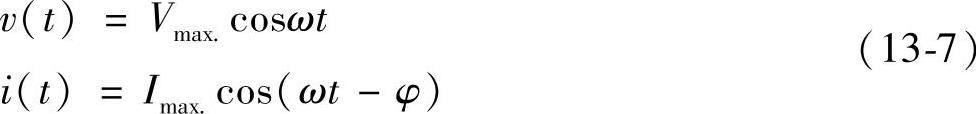
平均功率为：

假设二极管整流器的输出电流是恒定的，电压和电流的基波分量没有相位差。因此，平均功率可以写为：

为模拟这样的负载，可以采用电压幅值的小信号扰动方法。相应地，在流经负载的电流幅值中将产生小信号扰动。

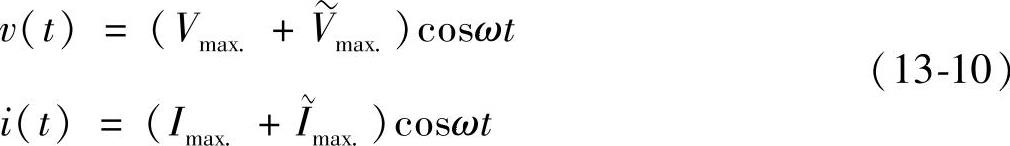
既然对于负载而言平均功率是恒定的，功率P亦可以写：

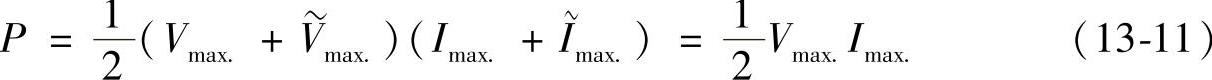
忽略二阶以上的高次项，有：

式（13-12）明确了负载的小信号特性。式（13-12）重写为：

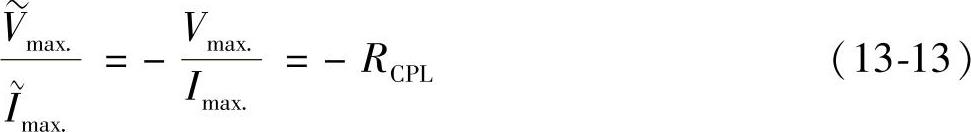
R_CPL定义为：

可见，考虑小信号扰动的交流恒功率负载由于负电阻特征。电阻的绝对值等于该工作点上恒功率负载的阻抗。图13-6是负载的小信号模型。

这个模型同样适用于单位位移变换器。具有单位位移系数的变换器，意味着负载电压和电流的基波分量是同相位的。所以，图13-6的模型亦适用于这类交流电力电子负载。通常这类变换器在二极管整流器后接有升压变换器，如图13-7所示。

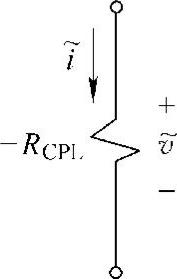
图13-6 前级二极管整流器的交流恒功率负载的小信号模型(www.xing528.com)

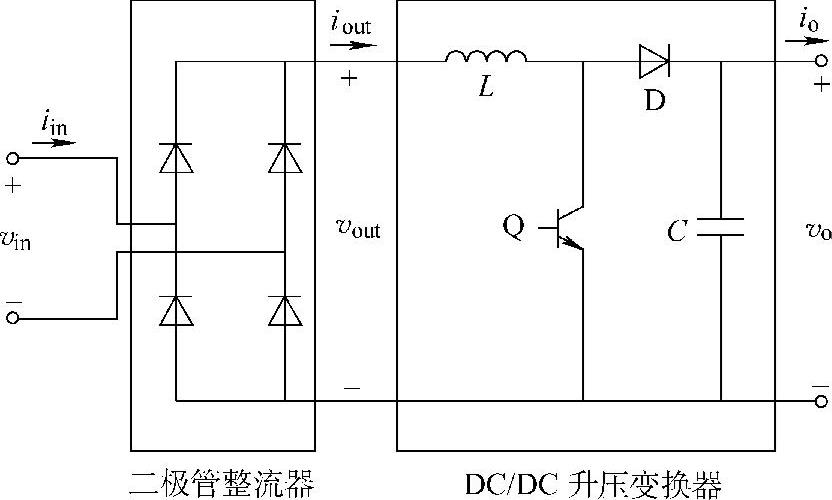
图13-7 前端带有升压变换器的二极整流负载（二极管整流器，DC/DC升压变换器）

这一节我们是假设变换器运行于连续导通模式，但是有些电力电子变换器是工作在非连续模式下，或者整流器后带有降压变换器（见图13-8）。因此，负载的输入电流是非连续的。图13-9为图13-8变换器的非连续电流示意图。

如果电压和基波电流是同相的，图13-6所示的小信号模型就是有效的。但是，如果电压和基波电流有相差，负载的小信号就是感性的。下一节将给出详细解释。

在这一节中，我们假设了输入电流的主要成分是基波。实际上，我们只考虑了电流的基波分量而不是实际的电流波形。实际的电流波形中包含其他谐波分量。若假设整流器的输出电流脉动很小，恒功率负载的电流将如图13-10所示。

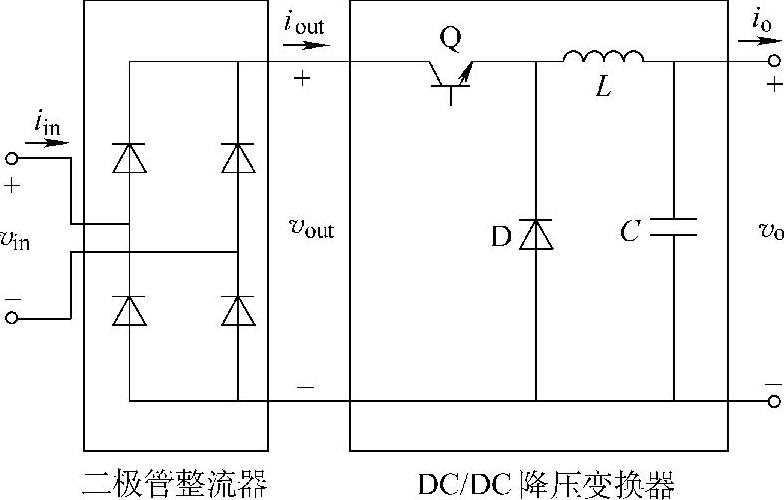
图13-8 前端带有降压变换器的二极管整流负载（二极管整流器，DC/DC降压变换器）

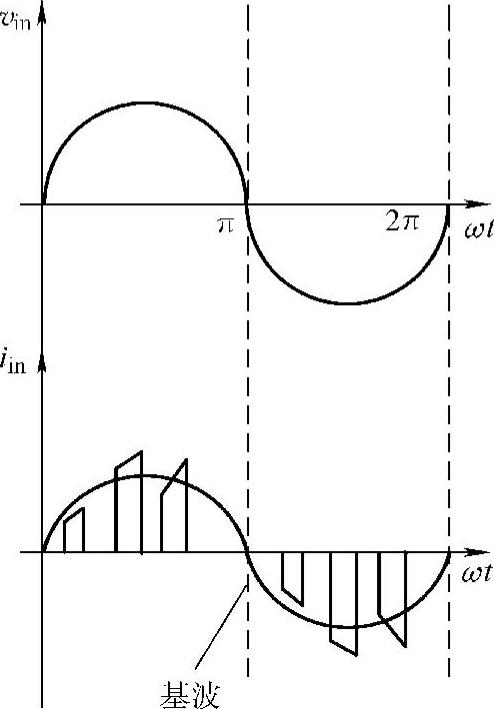
图13-9 图13-8变换器的输入电压和非连续电流

非正弦电流的傅里叶展开式为：

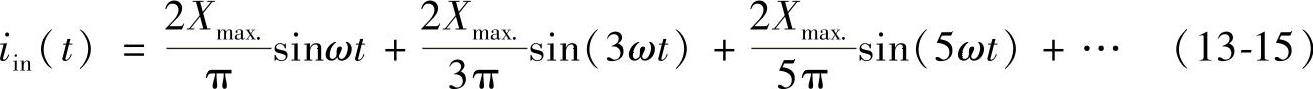
对于触发角为φ的可控整流器，正弦电压和非正弦电流表达式如下：

平均功率：

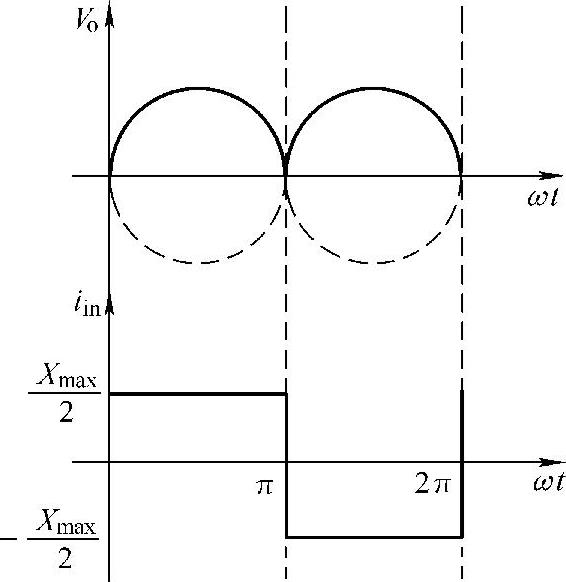
图13-10 恒功率负载的方波电流

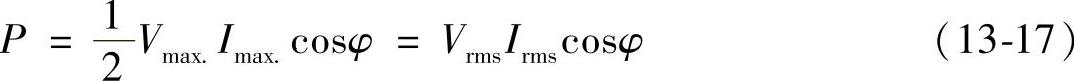
上式和式（13-8）是相同的。可以看出，只有基波电流参与了计算。这一节介绍的建模方法适用于正弦电压下的非正弦电流。非正弦电压可以采用广义状态空间平均法建模，对此将在13.4节详细介绍。