在连续导通模式下:当开关处于接通状态时的状态方程分别为
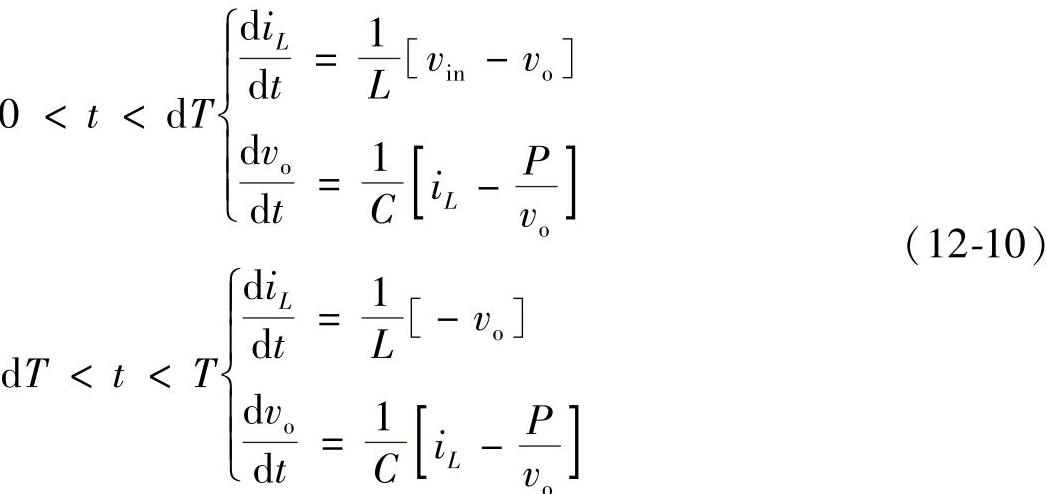
采用状态空间平均法[9~13],可得出
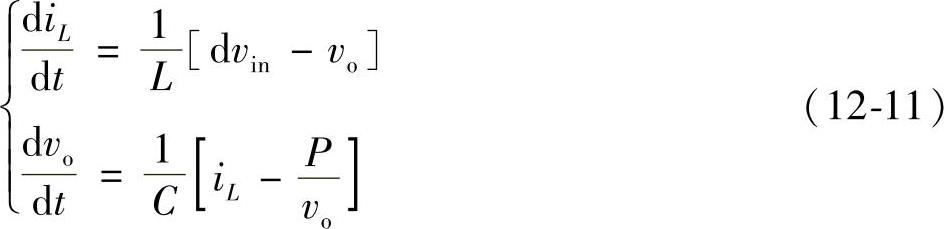
上式是非线性的。为研究图12-11所示的Buck变换器的小信号稳定性,假设输入电压和占空比分别受到小的扰动,由此导致的状态变量的扰动为
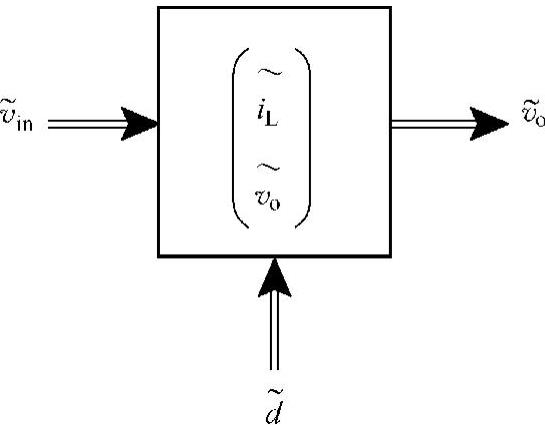
图12-12 降压变换器的小信号输入、输出及状态变量
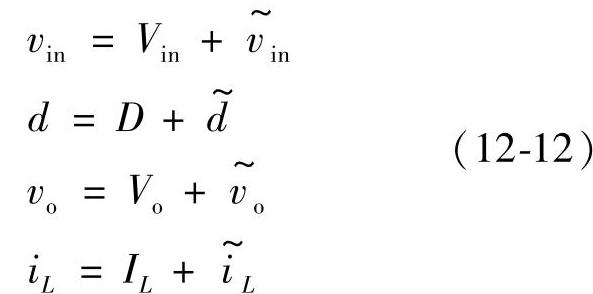
如图12-12所示,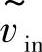 和
和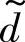 为输入,
为输入,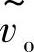 为输出,
为输出,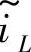 和
和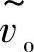 为Buck变换器小信号模型扰动的状态变量。小信号模型的稳定性可由传递函数和极点位置来确定:
为Buck变换器小信号模型扰动的状态变量。小信号模型的稳定性可由传递函数和极点位置来确定:
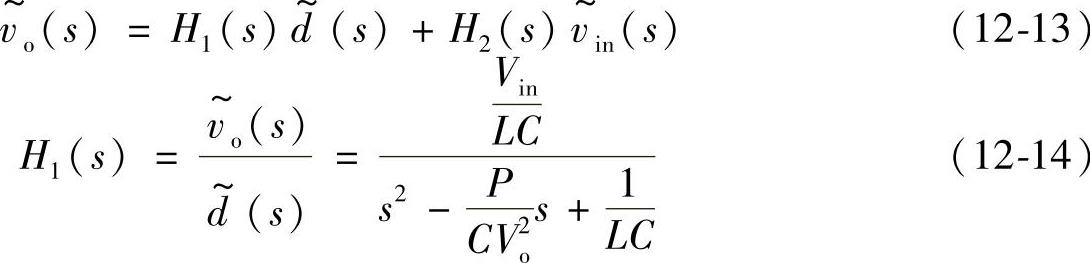
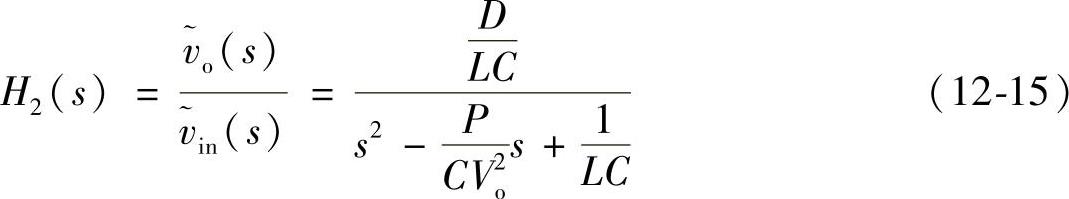
传递函数H1(s)和H2(s)极点的实部为正值。因此恒功率负载效应导致系统不稳定。图12-13为开环降压变换器的仿真示意图,其参数见表12-3,占空比为0.5。
表12-3 降压变换器参数

参考文献[3]研究了带恒功率负载的Buck变换器的动态特性;推导了线—输出和控制—输出传递函数和控制—输出传递函数;同时考虑了电压模式控制、电流模式控制、连续导通模式和断续导通模式。(https://www.xing528.com)
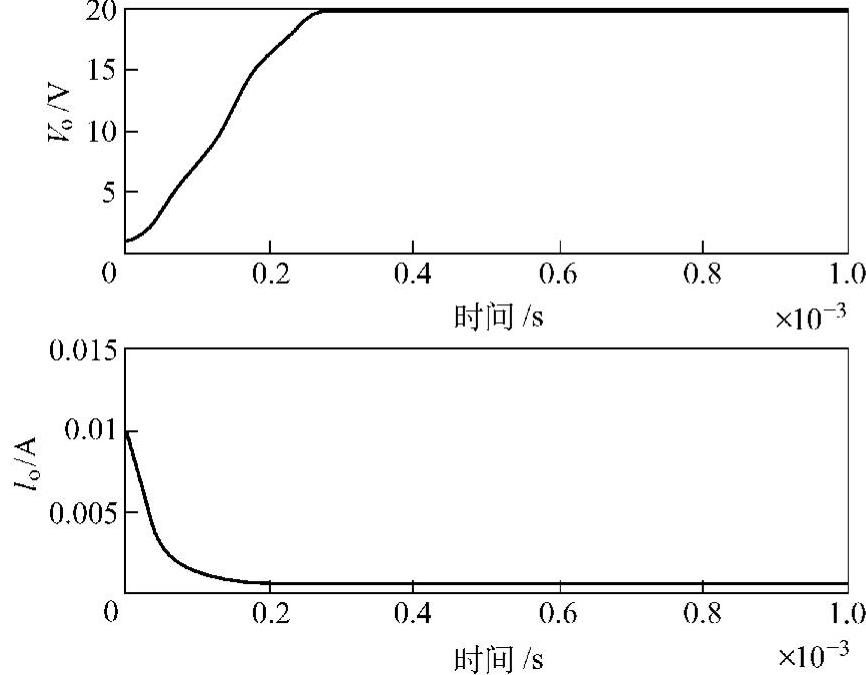
图12-13 开环降压变换器仿真(占空比为0.5)
还有另一种基于系统参数的非稳定问题,它对下节将要讨论的DC/DC变换器的稳定性至关重要。基于上述P、C、L、Vo、Io值,与图12-7类似,变换器很快变得不稳定。这种情况下,变换器甚至没有足够的时间改变开关状态。换句话说,不稳定发生的时间间隔非常短暂。在这么短暂的周期里电感电流几乎是恒定的(Iin)。图12-14为图12-11所示降压变换器发生超短时不稳定时的等效电路,其中假设在如此短的时间内电感电流基本不变。等效电路的状态方程如下:

求解该方程得
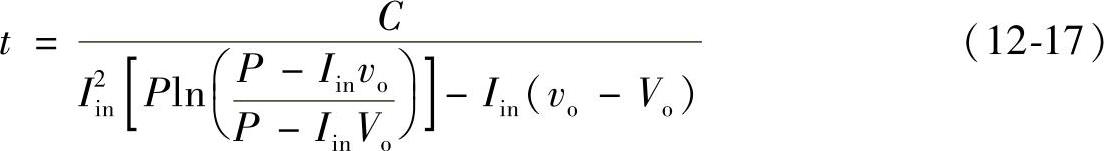
式中 t——时间。由式(12-16)和式(12-17),在t=t1时,如图12-15所示,
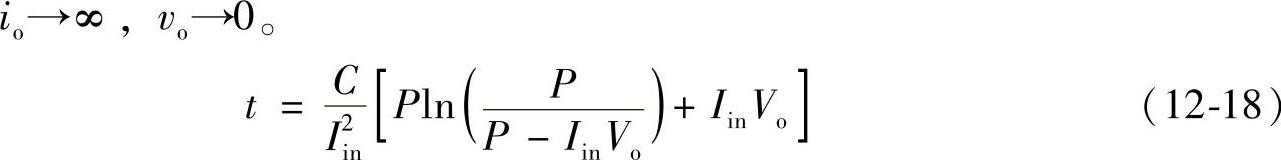
可见,带恒功率负载的系统是不稳定系统。其主要原因是不稳定发生的时间间隔小于开关周期。因此必须增加C和L的开关频率,并且应用滑模控制器(下节介绍)。
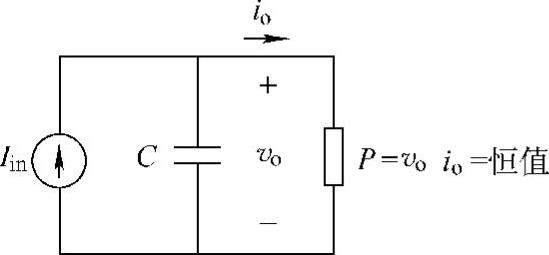
图12-14 降压变换器超短时不稳定的等效电路
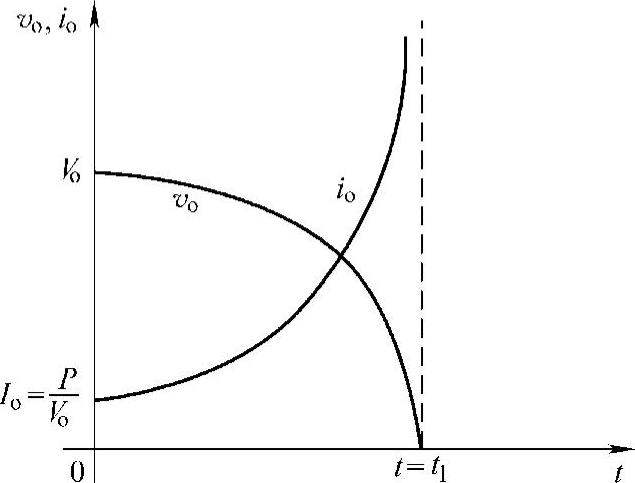
图12-15 图12-14所示电路的电压和电流波形
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




