稳定性分析仿真思路-车辆、航海、航空、航天运载工具电力系统

系统的稳定性分析通常采用线性化的状态空间模型。这种模型的使用依赖于保护的可靠性、电路的限制及为系统中每个电源和负载假设的稳定边界。假定这些稳定边界是为了防止单个负载出现大信号不稳定。通常的做法是导出小信号线性化等效电路并对系统进行仿真以确定系统的稳定性。至于是否需要此类仿真还存在问题。此类仿真在某些系统中确实没必要。Middlebrook的文章^［62］表明系统电源的输出阻抗和总的负载输入阻抗都是确定稳定性所必需的。根据双端口理论，如果小回路增益因子满足奈奎斯特稳定性判据，则系统是稳定的。图7-31所示为这种小信号稳定性判据中阻抗的普遍定义。T（s）=Z_S/Z_L即为小信号稳定性判据，它满足奈奎斯特稳定性判据。此外，参考文献［43］指出，当相位边界T（s）小于30°时，系统性能下降显著。

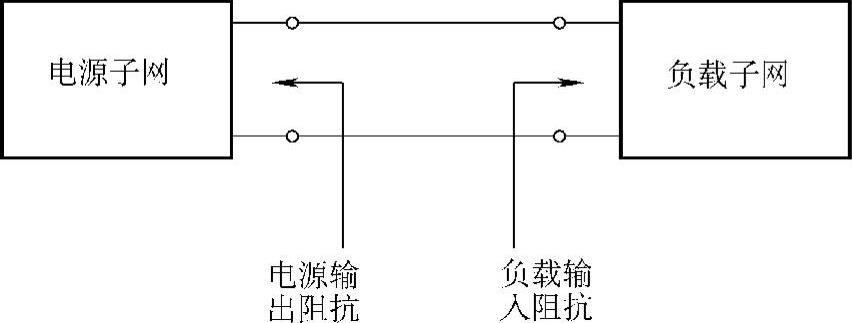
图7-31 电源输出和输入阻抗的定义

在考虑确定较大电力子系统小信号稳定性的方法时，阻抗特性没有系统中实际测量到的精确，由仿真模型得到的特性总是存在一些误差。因此只能根据电源和负载厂商的试验数据（如输入输出阻抗图）来确定系统小信号稳定性。这样做要比采用不精确的模型更准确，所以可以直接根据系统中实际使用的变换器厂商试验数据确定稳定性，这种方法很简单。

根据先前定义的子系统中实际负载的输入阻抗幅值和相位图，可计算出主总线上负载和布线的总并联输入阻抗。这种计算是逐点进行的，如频率在10～10kHz间的200点，一旦知道了单个子系统中负载的总并联输入阻抗和电源的总并联输出阻抗，Middlebrook所描述的方法^［62］就可用于确定系统的小信号稳定性。这是通过给出T（s）图来确定相位和增益边界。这种小信号稳定性研究的系统电源、负载及电缆阻抗如图7-32所示。

如果将图7-32中A点作为公共耦合点，则这个子系统总线的小信号分析依赖于满足奈奎斯特稳定性判据的T（s）：(www.xing528.com)

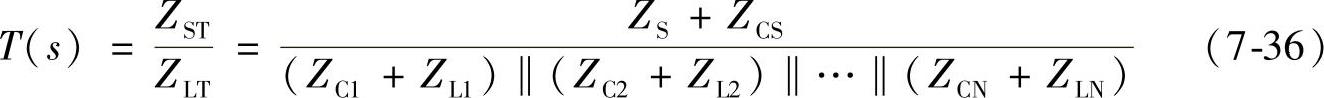
如果系统被定义为大信号模型，则线性状态空间模型显然不适用。为了保证整个系统性能仿真的精度，必须采用非线性系统模块的时域仿真。非线性系统模块包括保护电路和系统动态特性及约束，但并没有包括每个电源及负载变换器的非线性保护电路和实际反馈控制动态特性及约束（动态范围），这将造成大信号分析结果不准。

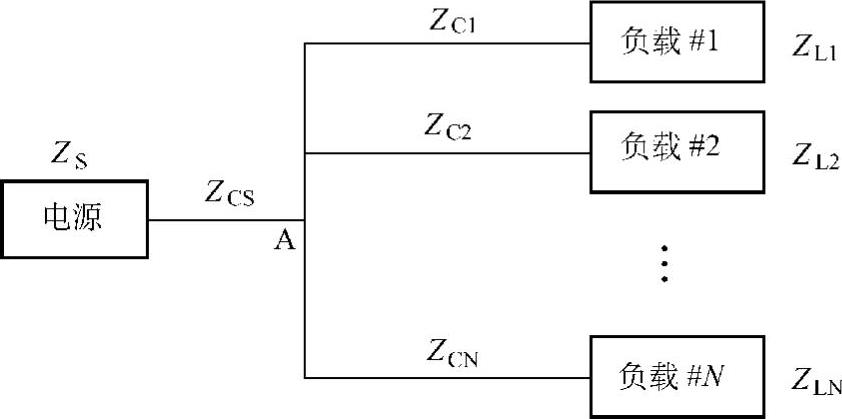
图7-32 数值小信号分析中阻抗的定义