车辆、航海、航空、航天运载工具电力系统稳定性定义

关于线性、非线性、离散和连续系统的稳定性有许多不同的定义。线性系统的稳定性分析通常采用以下经典方法：Routh-Hurwiz法、根轨迹法、波特图法和奈奎斯特判据法^{［60，61］}。另一个广为人知的线性或非线性系统稳定性分析方法是李普诺夫第二方法。但是，用这种方法推导许多非线性系统的李亚普诺夫函数难度较大。因此在确定一个大系统稳定性时需要依赖更多特定状态的定义。非线性系统稳定性的研究需要考虑初始状态、外部输入及其对系统中非线性元件的作用。就我们所知，对于非线性系统还没有一种普遍适用的分析方法。前面研究不同多变换器电力电子系统是基于线性系统稳定性分析技术^{［43～46］}，参考文献［46］中，基于线性PWM开关模型改变了开关变换器小信号线性模型的电阻R、电感L、电容C及直流分量值，然后用这样一个系统的相位边界来确定系统的稳定性。参考文献［43］提出了所研究系统的设计考虑，它基于电源及负载阻抗关系，采用了参考文献［62］导出的小信号系统稳定性分析。参考文献［43］在原型机及实际硬件的仿真和实验室测试中运用了大信号稳定性分析方法。

与李亚普诺夫法一样，本节稳定性定义考虑的是渐近稳定性。但我们不用为每个变换器或包含电源和负载变换器的较大系统找出一个合适的李亚普诺夫函数，而是考虑变换器输入和输出侧的电压和电流条件。我们所考虑的一种不稳定形式是一个或多个输入或输出电压或电流（信号）的发散，即它们从期望值变到公差带之外并在预先规定的时间内没有返回到公差带内，例如无界性。电力电子电路中的无界性不一定能被预测，如在Boost变换器开关失败时，它就可以导致供电总线的短路^［42］。这种类型的非线性不稳定不能用普通线性系统相位及增益边界法来预测。如果缺乏适当的保护和控制电路，这些类型的不稳定就会导致系统失灵。抖动是另一个不能被普通控制系统稳定性方法预测的非线性参数，它必须通过测试实际系统的硬件和电路得到。抖动实际上是由于缺少一种滞后机制所引起^［42］。由于热效应，抖动还可能导致元件失灵。混沌电力电子系统中另一个不稳定因素，表现为系统中一个或多个元素的伪随机函数。图7-30所示为紊乱的一种形式，它是系统中开关动作产生的确定性谐波噪声。它和外部噪声耦合在DC/DC变换器PWM电路的反馈环信号中，致使PWM的占空比发生随机变化。

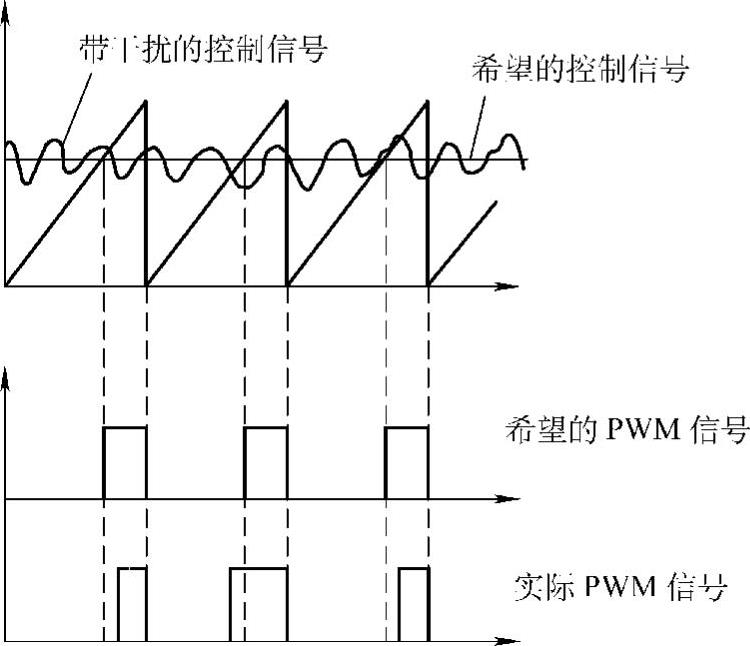
图7-30 混沌不稳定建模实例(www.xing528.com)

如之前所述，本节涉及的系统类型包括DC/DC电源变换器及多负载模块。DC/DC电源变换器给主DC总线供电。多负载模块包含许多不同的电力电子变换器，它们根据每个负载的需求产生不同的电压。通过对先前定义的子系统进行仿真有可能得到这种系统的稳定性和其他特性。所以最重要的问题就变成了怎样对单独的电源DC/DC变换器和负载模块进行建模及该采用频域方法还是时域方法。大信号、小信号和直流仿真是常用的仿真模型。状态空间平均和小信号线性化是最流行的建模方法。

众所周知，最常见的DC/DC变换器（如Buck、Boost和Buck-Boost）在连续和不连续导电模式下分别有两种和三种运行模式。如果开关频率较变换器动态控制的要求足够高，那就可以用平均法处理描述运行模式的状态空间方程。通常变换器增益分频频率设计得比开关频率的幅值至少低一个数量级，因此平均处理过的状态空间等效电路模型可用来对DC/DC变换器进行小信号仿真。平均处理过的状态空间等效电路是一个非线性、连续时间等效电路，它代表了原始的非线性脉冲（离散）系统。这个模型与大信号和小信号仿真均相关。但通常只对变换器和输入滤波器进行建模，而不对控制电路的动态特性和约束进行建模。总线故障、机械负载故障、负载变化引起的总线上极端的信号偏差、电子元件失灵等都可能导致大信号偏差。如果不考虑大信号偏差，那么只对线性化非线性状态空间平均模型线性化即可。线性化后得到一个只能用于小信号分析的系统模型。这意味着此模型只在遇到小扰动（如总线电压、电流、电子元器件和负载变化）时表现良好。如何才算“小”是由系统模型方程中其他系统参数决定的。

线性化去除了包含两个扰动乘积的项。显然，当一个或多个这样的项在系统模型中变得重要时，由于大偏差的出现，此模型就不再奏效。所以在设计DC/DC变换器控制电路和滤波器时选用的是小信号模型。然而，在它们用于系统稳定性分析时会有限制，这将在下节讨论。