食品质量管理：计量抽样检验方案

当质量特性是计量值时，衡量一批产品的质量有多种方法，其中最常见的是用批中所有单位产品的特性值的均值μ表示批质量的情况。根据用户对产品质量的要求，有的要求μ越大越好，即质量特性有下规格限，有的则要求μ越小越好，即质量特性有上规格限，也有的规定了质量特性的双侧规格限。下面分别各种情况进行讨论。

（一）计量一次抽样检验方案

我们假定质量指标X服从正态分布N（μ，σ2），由于μ通常是未知的，因而需要从该批产品中抽取n个产品测定其特性值，然后用样本的均值进行估计。

对不同的质量要求有不同的接收判断规则。

（1）对仅有上规格限的情况：由于要求指标值越小越好，因此可以定一个KU，当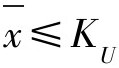时接收该批产品，否则就拒收该批产品。这时计量一次抽样检验方案可以用（n，KU（）表示。

（2）对仅有下规格限的情况：由于要求指标值越大越好，因此可以定一个KL，当时接收该批产品，否则就拒收该批产品。这时计量一次抽样检验方案可以用（n，KL）表示。

（3）对双侧规格限的情况：由于指标值不能太大也不能太小，要求其接近某规格值μ0，因此可以确定KL与KU，当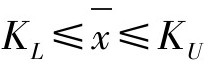时接收该批产品，否则就拒收该批产品。这时计量一次抽样检验方案可以用（n，KL，KU）表示。

（二）具有下规格限的计量标准型一次抽样检验方案

1.接收概率

对具有下规格限的抽样检验方案（n，KL）来讲，当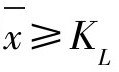时接收该批产品，否则就拒收，其接收概率是μ的函数，可以用L（μ）来表示。根据正态分布的性质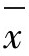，服从N（μ，σ2/n），当σ已知时有：当σ已知时有：

随着μ的增大，L（μ）也增大（图8-15）。

图8-15　具有下规格限的计量标准型一次抽样检验方案的OC曲线

2.抽样方案的确定方法

为制定计量标准型一次抽样检验方案要求同时控制两种错判的概率。因此为制定方案（n，KL），需要生产方与使用方协商两个质量指标的均值μ0、μ1（μ0＞μ1），从保护生产方利益的观点提出一个批质量指标均值μ0，当批质量指标均值≥μ0时，要求以大于或等于1-α的高概率接收；另外从保护使用方利益出发提出一个批质量指标均值μ1，当批质量指标均值≤μ1时，要求以小于或等于β的低概率接收，即

所以要制定一个计量标准型一次抽样检验方案，应该事先给定四个值：生产方风险α，使用方风险β，双方可以接受的合格批质量指标均值μ0与极限批质量指标均值μ1，按接受概率L（μ）是μ的增函数的特点，从下面两个式子中解出（n，KL）。

即

如我们记uα与uβ分别为标准正态分布的α与β分位数，有

当σ未知时，由于涉及t分布，这里略去计算公式。

【例8-9】对一批包装袋拉伸强度抽样检验，要求其拉伸强度越大越好。已知其服从正态分布，标准差σ=4kg/mm2。现已确定α=0.05，β=0.10，μ0=46kg/mm2，μ1=43kg/mm2。试制定计量标准型一次抽样方案。

所以，抽样方案为（16，44.31）：抽16个包装袋分别测其强度，其平均强度x≥44.31时，接收这批包装袋，否则拒收。如果我们从一批钢材中抽取16块，测得其强度的均值x=45.65，则应接收该批包装袋。

（三）对上规格限的情况

1.接收概率

对具有上规格限的抽样检验方案（n，KU）来讲，当≤KU时接收该批产品，否则就拒收，其接收概率也是μ的函数，同样用L（μ）来表示。根据正态分布的性质，x服从N（μ，σ2/n），当σ已知时有：

随着μ的增大，L（μ）减小（图8-16）。

图8-16　具有上规格限的计量标准型一次抽样检验方案的OC曲线

2.抽样方案的确定方法

与具有下规格限的情况类似，为同时控制两种错判的概率，在制定抽样检验方案时，需要生产方与使用方协商两个质量指标的均值μ0、μ1（μ0＜μ1）。

为了保护生产方利益，当批质量均值≤μ0时，要求高概率（≥1-α）接收。

为了保护使用方利益，当批质量均值≥μ1时，要求低概率（≤β）接收。

从上面两个式子中可解出（n，KU）：

（四）对双侧规格限的情况

1.接收概率

对于抽样方案（n，KL，KU）来讲，当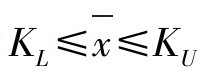时接收该批产品，否则拒收。接收概率仍然是μ的函数，也用L（μ）来表示。同样根据正态分布的性质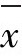，服从N（μ，σ2/n），当σ已知时有：

令μ0=（KU+KL）/2，K0=（KU-KL）/2；则KU=μ0+K0，KL=μ0-K0。从而

等价于等价于，所以判断规则转化为K0时接收，否则拒收。因此把抽样方案记为（n，K0），此时

当μ=μ0，μ0+d，μ0-d（d＞0）时，L（μ）的值分别为：

由此可见，L（μ）在μ=μ0时达到最大，且关于μ=μ0对称（图8-17）。(www.xing528.com)

图8-17　具有双侧规格限的计量标准型一次抽样检验方案的OC曲线

2.抽样方案的确定方法

由于抽样方案的OC曲线关于μ0对称，且在μ0达到最大，因此为制定抽样方案，可以用双方协商给出d0与d1，当μ0-d0≤μ≤μ0+d0时以高概率（＞1-α）接收，当μ≤μ0-d1或μ≥μ0+d1时以低概率（＜β）接收。

根据接收概率关于μ0的对称性，我们可以从如下等式中求解（n，k0）

这也就是要求：

要从中解出（n，K0）比较困难，下面我们给出一个近似解：

在σ已知，且时，有，从而由于

上述方程组可以近似表示为：

从中可解得：

（五）抽样检验表的使用

1.等价形式及说明

为使用方便，GB/T 8054-2008给出了计量标准型一次抽样程序及相关表格。为使标准适用于更多的场合，GB/T 8054-2008把抽样方案的表达形式进行一些改变（表8-8）。

表8-8　计量抽样检验方案的表达形式及其变形

下面以σ法为例，对其等价性进行说明。

（1）有上规格限的情况。

在α=0.05，β=0.10时，有uα=-1.645，uβ=-1.282。根据（n，KU）的计算公式，知

（2）有下规格限的情况。

同理，根据（n，KL）的计算公式，知

（3）有双侧规格限的情况。

2.使用步骤

（1）σ法：σ法的使用步骤列在表8-9中。

表8-9　“σ”法的使用步骤

续表

对【例8-9】，可以求得，查表2.5时A′在0.731～0.755，则（n，k）=（16，-0.411）。如令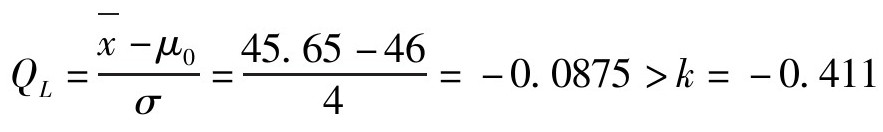，故予以接收。

（2）s法：当σ未知时，常用样本标准差s来估计σ，在GB/T 8054-2008中称此为s法，使用它们可以查得抽样方案。s法的使用步骤如表8-10所示。

表8-10　s法的使用步骤

【例8-10】设某种产品尺寸服从正态分布，其标准尺寸为100.0mm，如果批均值在100±0.2mm之内，则合格；如果在100±0.5mm之外，则不合格。已知批标准差σ=0.3mm，试求抽样方案。（取α=0.05，β=0.10）

解：由于σ已知，利用查表方法的步骤如下：

首先，计算

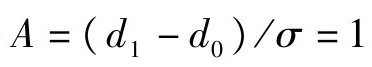，所在范围为0.980～1.039，查得n=9；

由于c=2d0/σ=1.333，所在范围为0.867以上，接收常数k=-0.548；

故

时接收该批产品，否则拒收。

如果现在抽取了9个样品，求得其样本均值为100.4，那么

故拒收该批。