食品质量管理：控制图应用举例

（一）计量控制图

在计量控制图中，常用的典型控制图有均值-极差控制图、均值-标准差控制图和单值-移动极差控制图。下面重点介绍它们的使用方法。

1.均值—极差控制图

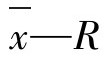控制图是计量控制图中最常用、最重要的控制图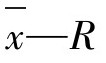，控制图具有以下两个特点。

（1）适用范围广。图：若x服从正态分布，则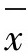也服从正态分布；若x非正态分布，则根据中心极限定理，当样本量充分大时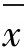，近似服从正态分布。关键是这后一点才使得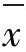图得以广为应用。因此，可以说只要是计量值数据，应用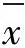总是没有问题的。R图：通过在计算机上的统计模拟试验证实：只要x不是非常不对称的，则R的分布无大的变化，故适用范围也比较广。

（2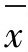）图灵敏度高。由于正常波动的存在，一个样本组的各个x的数值通常不会都相等，有的偏大，有的偏小，这样把它们加起来求平均值，正常波动就会抵消一部分；但对于异常波动，由于一般异常波动所产生的变异往往是同一个方向的，故求平均值的操作对其并无影响。因此，当异常时，描点出界就更加容易了，也即灵敏度高。

【例5-5】某植物油生产厂，采用灌装机灌装，每桶标称重量为5000g，要求溢出量为0～50g。采用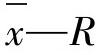控制图对灌装过程进行质量控制。控制对象为溢出量，单位为g。

解：第1步，取得预备数据。取样分组的原则是尽量使样本组内的变异小（由正常波动造成），样本组间的变异大（由异常波动造成），这样控制图才能有效发挥作用。因此，取样时，组内样本必须连续抽取，而样本组间则间隔一定时间。本例每间隔30min在灌装生产线连续抽取n=5的样本计量溢出量。共抽取25组样本，将数据记入数据表（表5-4）。

表5-4　溢出量控制图数据表

第2步，计算每一组数据的平均值

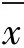和极差R，记入表5-4中。

第3步，计算25组数据的总平均值

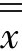和极差平均值。

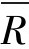第4步，计算控制界限。根据表5-2可知，R图的控制限为：

第5步，作图并判断过程的稳定性。根据以上参数作R控制图（图5-17）和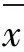控制图（图5-18），并将表5-4中的数据在相应控制图上打点。

对照常规控制图的判异准则，可判R图和

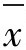图均处于稳态。

图5-17　分析用溢出量极差控制图

图5-18　分析用溢出量平均值控制图

第6步，计算过程能力指数（过程能力指数的概念与计算方法详见本章第三节）。

因此，过程能力差，不合格品率高，需提高成能力，减少不合格品率。

2.单值—移动极差控制图

【例5-6】某发酵厂每半小时对发酵醪进行温度测定，结果如表5-5所示。表中x表示测定的温度值，RS代表移动极差。请制作控制图并对过程进行判定。

表5-5　发酵醪温度测定值及统计表

解：根据单值—移动极差控制图计算公式（表5-2），得到：

按照作图程序，得到移动极差控制图（图5-19）和单值控制图（图5-20），图中样本点数字表示该点为异常点及其判断准则）。

图5-19　分析用发酵醪温度移动极差控制图

图5-20　分析用发酵醪温度单值控制图

从图5-19中可见，从第6点开始直到第14点，连续9点落在中心线的同一侧，依据判异准则的准则2，属于异常链；第22点超出上控制限，属于异常。从图5-20中可见，第5点和第21点分别超出上、下控制限，属于异常；第6点至第11点连续6点递减，符合判异准则的准则3，属于异常链。综合以上判断，发酵醪温度控制过程出现异常，应尽快查找异常原因并加以消除；然后再重新收集25个数据制作控制图，以判定过程的稳定性。

（二）计件控制图

在计件值控制图中，常用的典型控制图是不合格品数控制图（nP图）和不合格品率控制图（P图）。计件值通常服从二项分布，故在计算计件值控制图的控制界限时，要用到二项分布的性质。

1.不合格品数控制图（nP图）

nP图用于不合格品数的控制，通过观察产品不合格品数nP的变化来控制产品质量。由于当样本量n变化时nP控制图的控制线都成为凹凸状，不但作图难，而且无法判异、判稳，故只在样本量相同的情况下，方才应用此图。

由概率论知道，不合格品数服从二项分布，其总体特征参数为：

由于P通常不知道，一般用k个样本不合格品数的平均值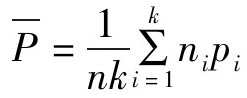（nipi为第i组样本中的不合格品数）来估计。当nP≥5时，二项分布近似正态分布（故使用nP图时，n往往都比较大，一般取n≥50），根据正态分布的3σ原则，nP图的控制界限为：

【例5-7】某食品厂计划对糖果单粒包装机的包装质量进行控制。现每半小时取100粒糖果进行包装外观检验，结果见表5-6。请作nP图并判定过程是否处于统计控制状态。

表5-6　某食品厂糖果单粒包装产品的质量状况

第1步，收集数据，从过程中随机抽样25组，每组100个，记录其中的不合格品数，填入表5-6。

第2步，计算样本平均不合格品率：

计算样本平均不合格品数：n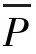=100×2.72%=2.72

第3步，计算控制界限：

第4步，根据以上数据作图并打点，见图5-21。

图5-21　糖果包装不合格品数控制图

图5-21显示，糖果单粒包装机工作过程处于统计控制状态。

2.不合格品率控制图（P图）

P图用于不合格品率的控制，通过观察产品不合格品率P的变化来控制产品质量。P图主要使用在样本数量不相等的情况（当然，样本数量相等也可使用）。

由概率论知道，不合格品率服从二项分布，其总体特征参数为：

由于P通常不知道，一般用k个样本不合格品数的平均值P来近似。根据正态分布的3σ原则，P图的控制界限为：

式中，P表示样本平均不合格品率，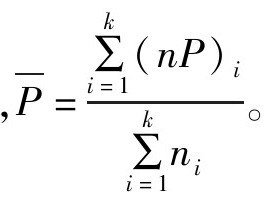

使用P图的注意事项：若P很小，则样本量n应充分大，使得nP≥1，以免经常出现不合格品数为零，造成过程正常的误解。故通常取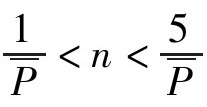。从数学的观点来看，样本量n要取到25/P方能认为二项分布是充分近似常态分布的。但这样做，样本量要比5/P大5倍，太不经济，故休哈特控制图的国标规定按照式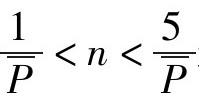进行。这说明我们在现场要推行的是SPC与SPD工程，而非SPC与SPD数学。(www.xing528.com)

【例5-8】某食品厂4月份某种产品质量的检测结果如表5-7所示。根据以往的记录知，稳态下的过程平均不合格品率P=0.0389，试设计P控制图对其进行控制。

表5-7　某种产品质量的检测结果

第1步，收集数据，样本数不少于25组，本例从过程中随机抽样28组数据。

第2步，计算每组的不合格品数，填入表5-7第（3）栏。

第3步，计算每组样本不合格品率，列于表5-7第（4）栏。

第4步，计算过程平均不合格品率：

第5步，计算控制限：

由于每个样本的大小ni不相等，所以必须对每个样本分别求出其控制界限，列于表5-7第（5）栏和第（6）栏。

第6步，画控制图。以样本序号为横坐标，样本不合格品率为纵坐标作P图，并根据每个样本的不合格品率Pi，在控制图上描点，如图5-22所示。

图5-22　某产品不合格品率控制图

第7步，判稳。由图5-22知，第27个样本的点子出界，所以过程失控，需要找出异常因素并采取措施保证它不再出现。由于图5-21中，UCL呈凹凸状，故对界内点不能判异、判稳，必须采用通用不合格品数控制图，方能进行判异、判稳（参见后面的通用控制图）。

（三）计点控制图

在计点值控制图中，常用的典型控制图是不合格数控制图（c图）和单位不合格数控制图（u图）。当样本大小固定不变时，常用c图；当各个样本的检验单位无法固定时，就需要将各个样本的不合格数折算成标准单位的不合格数来进行控制，这时就只能使用u图。通常计点值服从泊松分布，故在计算计点值控制图的控制界限时，会用到泊松分布的性质。下面以c图为例来说明计点值控制图的设计。

由概率论知道，泊松分布的一个显著特性就是：均值与方差相等，即μ=σ2=λ。若λ未知，可用样本的平均不合格数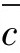进行估计。根据3σ原则，c图的控制界限为：

【例5-9】已知某铸件一定面积（n=10cm2）的不合格数的统计数据如表5-8所示，试绘制c图。

表5-8　某铸件单位面积不合格数统计表

第1步，计算平均不合格数，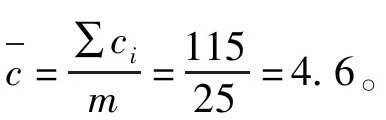

第2步，计算控制界限：

第3步，画控制图（图5-23）。

图5-23　铸件不合格数控制图

（四）通用控制图

世界各国的控制图大多采用3σ方式。在应用控制图时，需要计算控制图的控制界限并根据实测数据计算出所控制的统计量，在控制图中描点。这两项都需要一定的工作量，尤其是P图、u图，由于控制界限计算公式中含有样本大小n，控制界线随着n的变化而呈凹凸状，作图十分不便，也难以判稳、判异。

1981年，我国张公绪教授与阎育苏教授提出的通用控制图解决了上述问题。在通用控制图上，控制界线是直线，而且判断异常的结果也是精确的。

1.通用控制图的原理

所谓随机变量的标准变换是指经过变换后随机变量的平均值变成0、方差变成1的变换，即变换后的随机变量=（随机变量-μ）/σ。

这是可以理解的。随机变量减去其平均值后的平均值应为0；分母为标准差，也就是说用标准差作尺度，这样，变换后的标准差应为1。

现在，对控制图控制限的3σ方式进行标准变换，于是得到：

式中，下标“T”表示通用的“通”。

这样，任何3σ控制图都统一变换成上下控制限分别为+3、-3，中心线为0的通用控制图。通用图的优点是控制界限统一成3、0、-3，可以事先印好，简化控制图，节省管理费用，在图上容易判断稳态和判断异常。

通用图的缺点是在图中打（描）点也需要经过标准变换，计算要麻烦些。

2.标准变换

（1）均值-极差控制图。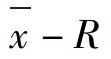控制图常采用的变量是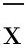，可引入以下标准变换：

（2）不合格品率控制图和不合格品数控制图。在通用图上，P图与nP图恒等，证明如下：

式中，P为样本不合格品率，n为样本大小，d为样本不合格数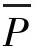，为过程不合格品率。

因此，对休哈特P图与nP图而言，在PT图与nPT图中应选nPT图来做，这样可直接利用现场的不合格品数据，不需要再去计算不合格品率。

（3）不合格数控制图和单位不合格数控制图。在通用图上，c图与u图恒等，证明如下：

式中，u为样本的单位不合格数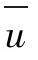，为样本平均单位不合格数，n为样本检查单位，c为样本不合格数，为过程平均不合格数。

因此，对休哈特c图与u图而言，在cT图与uT图中应选cT图来做，这样可直接利用现场的不合格数数据，不需要再去计算平均单位不合格数。

【例5-10】同【例5-8】，请利用通用控制图对其过程进行控制，并比较通用图的优缺点。

解：PT图与nPT图恒等，所以，我们选择nPT图来作图。用Excel对不合格品数进行标准化转换，以3、-3为上、下限，转换结果如表5-9所示，绘制标准化控制图如图5-24所示。

表5-9　标准化转换结果

续表

图5-24　某产品nPT控制图

将本例nPT图与【例5-8】P图对比，可见二者的形态是相同的。但应用通用图要方便得多。从图5-24，还可看出下列判异之处：

（1）第27点出界，见判异准则1——1点落在A区以外；

（2）第22、24点在A区，第24、26点在A区，见判异准则5——连续3点中2点在A区；

（3）第5至第15点为11点链，见判异准则2——连续9点在中心线一侧；

（4）第9至第13点，见判异准则6——连续5点中4点在B区。