食品质量管理中的过程质量统计推断

总体与从中抽取的样本之间的关系是统计学的中心内容。对这种关系的研究可从两方面着手：一是从总体到样本，这就是研究抽样分布的问题；二是从样本到总体，这就是统计推断问题。统计推断是以总体分布和样本抽样分布的理论关系为基础的。为了能正确地利用样本去推断总体，并能正确地理解统计推断的结论，须对样本的抽样分布有所了解。

由总体中随机地抽取若干个体组成样本，即使每次抽取的样本含量相等，其统计量（如x，S）也将随样本的不同而不同，因此样本统计量也是随机变量，也有概率分布。我们把统计量的概率分布称为抽样分布。

由总体随机抽样的方法可分为有返置抽样和不返置抽样两种。前者指每次抽出一个个体后，这个个体应返置回原总体；后者指每次抽出的个体不返置回原总体。对于无限总体，返置与否关系不大，都可保证各个体被抽到的机会均等。对于有限总体，要保证随机抽样，就应该采取返置抽样，否则各个体被抽到的机会就不均等。

在质量管理中，常用的是样本均值的抽样分布，下面重点介绍。

设有一个总体，总体均数为μ，方差为σ2，总体中各变数为x，将此总体称为原总体。现从这个总体中随机抽取含量为n的样本，样本平均数记为。由这些样本算得的平均数有大有小，不尽相同，与原总体均数μ相比往往表现出不同程度的差异。这种差异是由随机抽样造成的，称为抽样误差。显然，样本平均数也是一个随机变量，其概率分布叫作样本平均数的抽样分布。由样本平均数构成的总体称为样本平均数的抽样总体，其平均数和标准差分别记为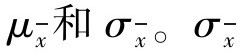是样本均数总体的标准差，简称样本标准误。统计学上已证明总体的两个参数与x原总体的两个参数有如下的关系：

x变量与变量的概率分布间的关系可由下面的定理说明。(www.xing528.com)

（1）若随机变量x服从正态分布N（μ，σ2），则随机样本x1，x2， ... ，xn的统计量x的概率分布服从N（μ，σ2/n）的正态分布。

（2）若随机变量x服从平均值为μ和方差为σ2的非正态分布，则随机样本x1，x2， ... ，xn的统计量的概率分布，当n相当大时，逼近N（μ，σ2/n）的正态分布。这就是中心极限定理。

上面的两个定理说明样本平均值的分布服从或逼近正态分布。

中心极限定理告诉我们，不论x服从何种分布，一般只要n＞30，就可以认为的分布是正态的。若x的分布不是很偏斜，在n＞20时，的分布就近似正态了。这就是正态分布较其他分布应用广泛的原因。

在实际工作中，总体标准差σ往往是未知的，因而无法求得。此时，可用样本标准差S估计σ。于是以估计。记为，称作样本标准误或均数标准误。是平均数抽样误差的估计值。若样本中各观察值为x1，x2， ... ，xn，则