圆锥表面上的点和线-建筑制图技巧

1.圆锥表面上的点

由于圆锥面的投影没有积聚性，所以圆锥表面求点要用包含该点作辅助素线法或辅助纬圆的方法来作图。

【实例分析】例5-7 如图5-17a所示，在圆锥表面上有A、B、C三个点，已知它们的正面投影，求其他两面投影。

解：如图5-17b所示，作图步骤如下：

1）连接已知点A和锥顶S的正面投影s′a′并延长交底面圆周于点1′，则S1就是构造的辅助素线，点A在该素线上。因为（a′）在左边且不可见，则点A在左后锥面上。由1′向底面圆周水平投影的左后圆周上引“长对正”得到1，连接s1，则a必在s1上。由（a′）向该素线的水平投影s1引“长对正”得到a，再由a、a′求出a″。由于点A在左半锥面，a″可见。

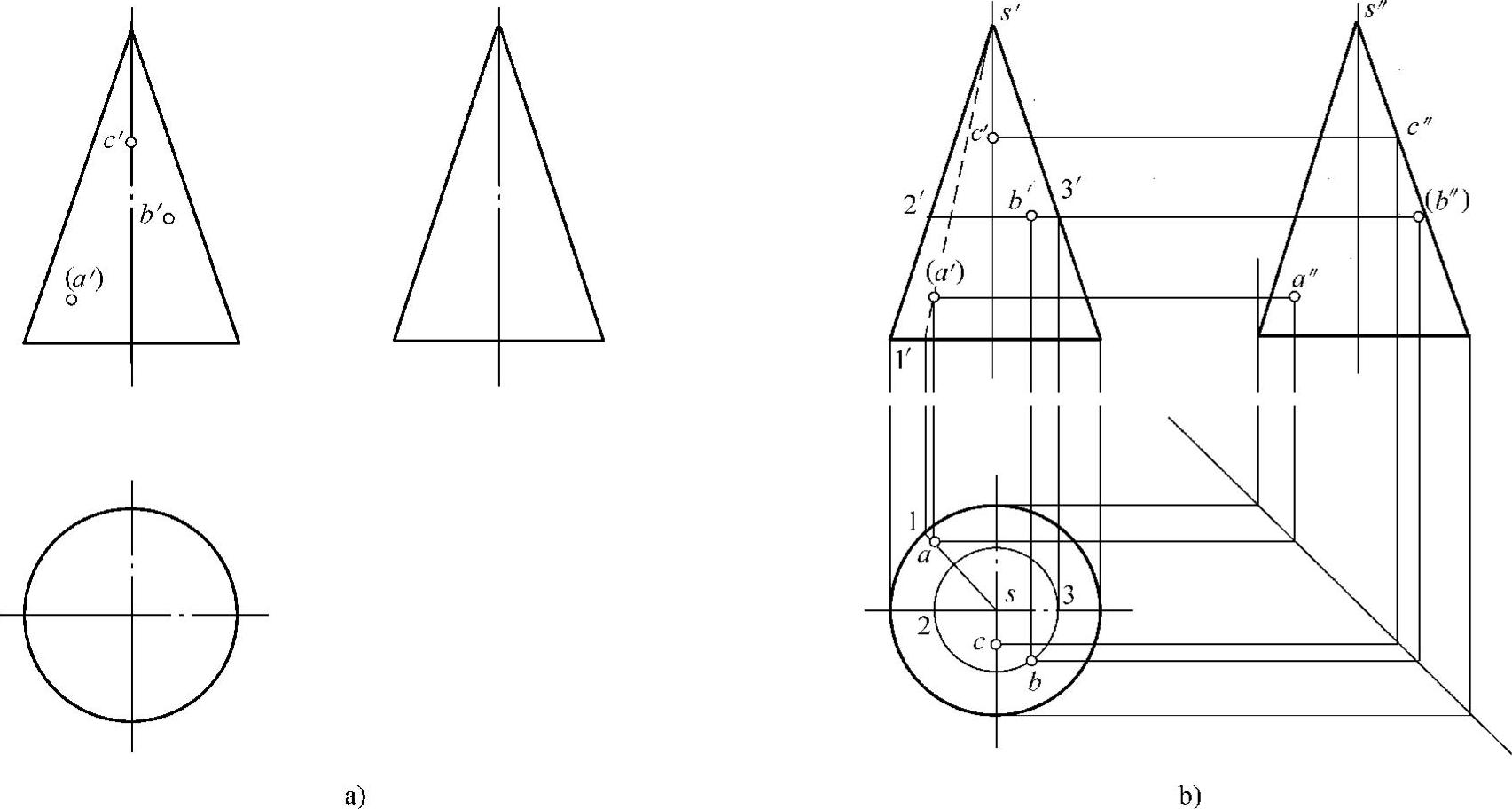
图5-17 圆锥表面求点

2）过已知点B在圆锥表面作一个与底面圆平行的辅助纬圆，该纬圆的水平投影反映实形，正面和侧面投影积聚为直线。即过正面投影b′作纬圆的正面投影2′3′（其投影积聚为一条平行于底面的水平线，并与最左、最右素线交于点2′、3′，该水平线2′3′的长度等于该纬圆的直径），然后由2′、3′分别向最左素线、最右素线的水平投影引“长对正”得到2、3。以s为圆心，s2或s3为半径即可画出该纬圆的水平投影，则b必在该纬圆上。因为b′可见，则由b′向纬圆水平投影的前半圆周上引“长对正”得到b，再由b′、b求出b″。由于点B在右半锥面上，所以（b″）不可见。

3）由c′向最前素线的侧面投影引“高平齐”得到c″，再由c″向最前素线的水平投影引“宽相等”得到c。(www.xing528.com)

2.圆锥表面上的线

圆锥底面上的线是直线，方法同平面体表面求线。而圆锥面上的线有三种情况：直线、圆弧、非圆曲线。

1）当圆锥面上的线或延长线过锥顶时，该线为直线。只需求出该直线的两个端点，连线即可。

2）当圆锥面上的线垂直于圆锥轴线时，该线为圆或圆弧。就需要找出圆心，并求出该圆弧的起点与终点，画圆弧。

3）当圆锥面上的线倾斜或平行于圆锥轴线时，该线为非圆曲线。则需要求出该非圆曲线上的点，进行非圆曲线的描绘。在这里需要注意的是，非圆曲线的起点、终点、转向轮廓线上的点必须求，为了让非圆曲线更加准确，可以适当补充一些中间点。

所以圆锥表面上求线的方法实际上也是圆锥表面上求点方法的运用。在可见表面上的线可见，画粗实线；在不可见表面上的线不可见，画虚线。

【实例分析】例5-8 如图5-18a所示圆锥，在圆锥面上有一线段，已知其正面投影，求其他两面投影。

解：由于该线段与轴线倾斜，因此为一非圆曲线段。要求该曲线段的投影，先求出该线段上一系列点的投影，再将这些点的投影依次光滑连接起来即可。在该线段上取两个端点1′、3′，取最前素线上的点2′，由于2′和3′之间的距离较长，为了使曲线更加准确，最后在它们中间取点4′。点1位于圆锥左前锥面，点4位于圆锥右前锥面，是两个一般位置点。根据圆锥表面求点的方法，利用辅助纬圆法求出点1的水平投影，利用辅助素线法求出点4的水平投影，再用“知二补三”的方法求出它们的侧面投影。点2位于最前素线，点3位于最右素线，是两个特殊位置点。由2′向最前素线的侧面投影引“高平齐”求得2″，再由2″向最前素线的水平投影引“宽相等”求出2；由3′向最右素线的水平投影引“长对正”求得3，再由3′向最右素线的侧面投影引“高平齐”求得3″。最后光滑地将各面投影分别连接起来，注意位于右半锥面部分的侧面投影2″（3″）不可见，画虚线；而位于左半锥面部分的侧面投影1″2″可见，画实线。作图步骤如图5-18b所示。