1.平面上的点和直线
条件一:如果一点在平面的任意一条直线上,那么该点在该平面上。
条件二:如果一条直线通过平面上的任意两点,或者通过平面上的一点并且平行于该平面上的另一条直线,那么该直线在该平面上。
如图5-5a所示,已知平面△ABC及其上一点D的正面投影d′,要保证D在平面△ABC上,就要让该点在平面的一条直线上。那么我们就来构造这条平面上的直线,要保证一条直线在平面上,根据条件我们可以有两种方式构造:
第一种方式如图5-5b所示,过平面上的两点A、D构造直线AD(正面投影为a′d′),则AD就是该平面上的一条直线,延长后必然和平面上的另一条直线BC相交,交点为E(正面投影为e′)。根据从属性,点E在直线BC上,那么它的水平投影e必在该直线的水平投影bc上。过e′作长对正,交bc于点e,连接ae。因为点D在直线AE上,那么d必在ae上,过d′作长对正,交ae于点d。
第二种方式如图5-5c所示,过平面上的点D做直线MN//AC,则直线MN是平面上的一条直线。根据平行性,作正面投影m′n′//a′c′,与a′b′、b′c′的交点分别为m′、n′。根据从属性,过点m′、n′作长对正,交ab、bc分别为m、n,连接mn。点D在直线MN上,过d′作长对正交mn于点d。
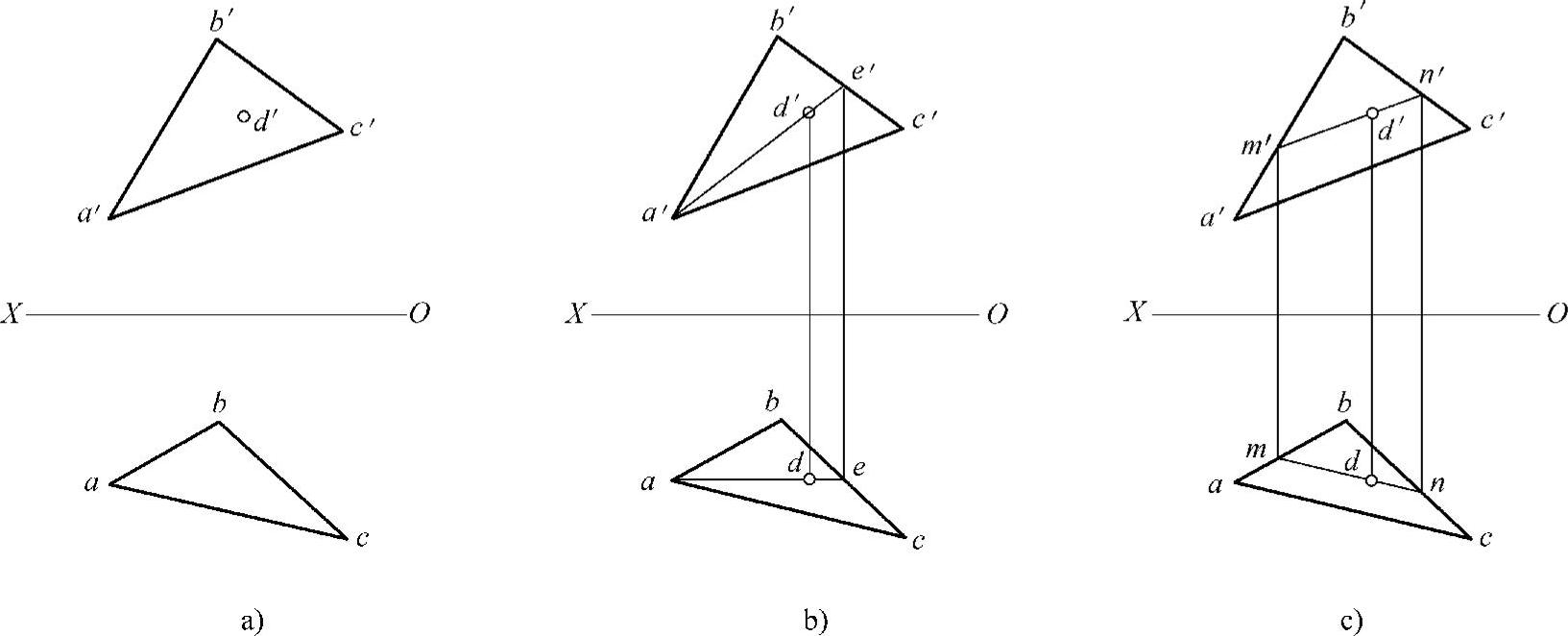
图5-5 平面上的点和线
2.棱柱体表面上的点
由于棱柱体属于平面立体,所以棱柱体表面上求点与平面上求点的方法相同。由于棱柱柱面有积聚性投影,可以利用积聚性投影作图。只是需要注意立体表面的多层性,投影图上必须分清待求点是在哪个平面上,才能确定点的投影位置,并且判别投影的可见性。
【实例分析】例5-1 如图5-6a所示,在六棱柱表面上有点A、B,已知它们的正面投影a′、b′,求A、B两点的水平投影和侧面投影。(https://www.xing528.com)

图5-6 六棱柱表面上求点
解:a′在六棱柱正面投影左边的矩形中,左边矩形是六棱柱左前、左后棱面的投影的重影。再根据a′可见,判定点A位于六棱柱的左前棱面上。而六棱柱棱面的水平投影均有积聚性,积聚为水平投影中六边形的边,分别对应六个棱面。那么左前棱面的水平投影积聚为六边形的左前边,故a也应对应其上。由a′向六边形左前边上引“长对正”,得到水平投影a,再根据点的知二补三即可求得侧面投影a″,最后分析点A位于左棱面判断a″可见。点B的求法与点A类似,由于(b′)位于右边的矩形且不可见,判定点B位于六棱柱右后棱面上,则水平投影b对应于六边形的右后边上,由(b′)向六边形右后边上引“长对正”求出b,再根据点的知二补三求得侧面投影b″。最后分析点B位于右棱面判断(b″)不可见,如图5-6b所示。
这种表面求点法称为积聚性求点法,要点是向面的积聚性投影上引线求得第二个投影。
3.棱柱体表面上的线
平面体表面上的线的投影仍然是直线。棱柱体表面上求线实际上是棱柱体表面上求点方法的运用,只要求出直线端点的投影,连线即是该直线的投影。在可见表面上的线可见,画粗实线;在不可见表面上的线不可见,画虚线。
【实例分析】例5-2 如图5-7a所示,已知五棱柱表面上一线段的正面投影,求其水平投影和侧面投影。
解:该线段在五棱柱的左前棱面、右前棱面上,是由两条直线段组成的空间折线。那么把该线段分解为左前棱面、右前棱面上的两条直线段AB、BC,分别求取。用积聚性求点法求端点A、B、C的投影,分别将直线段AB、BC的同面投影连线,即水平投影ab、bc,侧面投影a″b″、b″(c″)。水平投影均可见,ab、bc画粗实线。而AB在左侧棱面上可见,侧面投影a″b″画粗实线;BC在右侧棱面上不可见,侧面投影b″(c″)画虚线,如图5-7b所示。
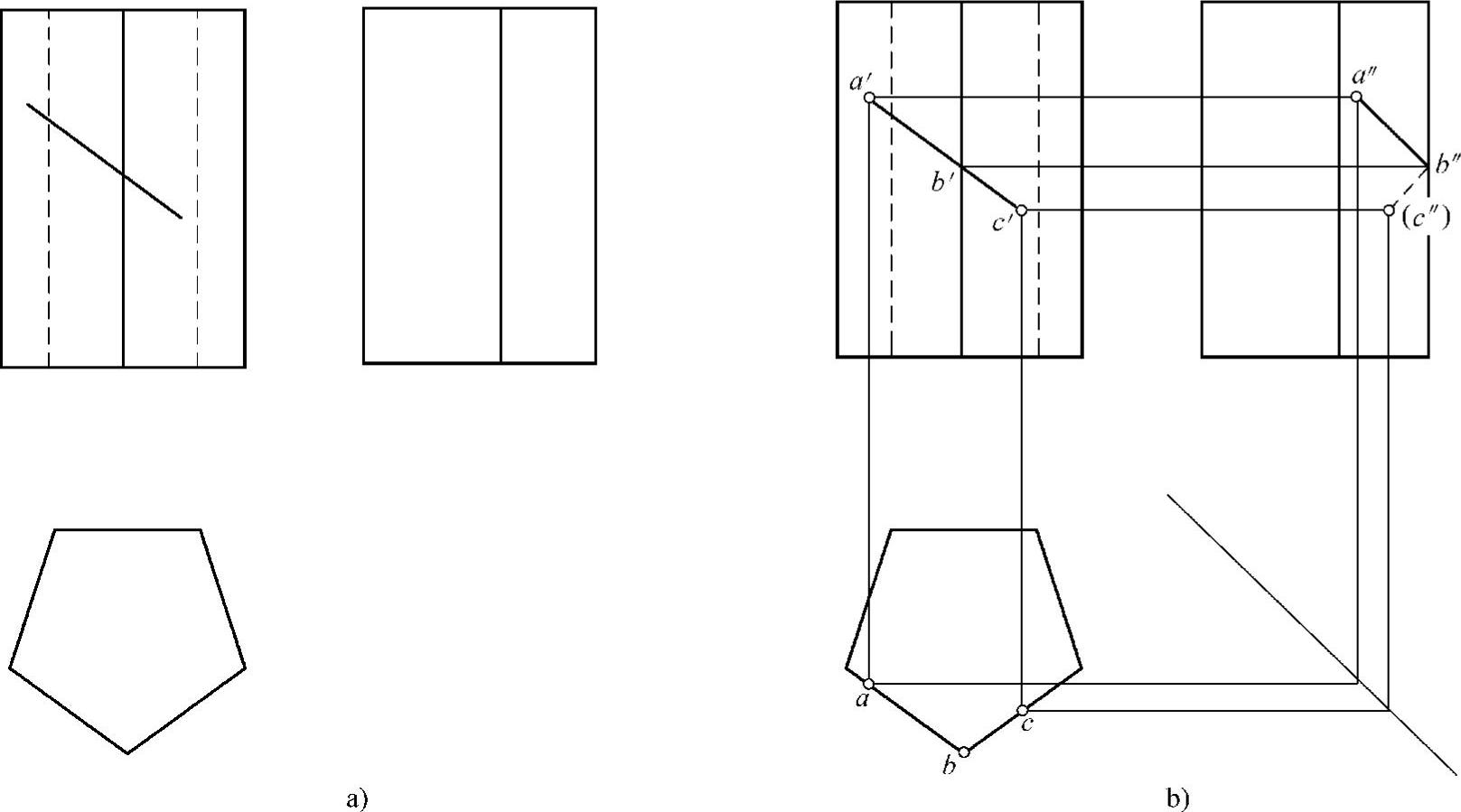
图5-7 五棱柱表面上求线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




