建筑制图中点的投影与直角坐标

1.点的投影与直角坐标的关系

空间点A可以用坐标（x，y，z）来表示。如图4-3所示，若把三个投影面看做三个坐标面，则三投影轴就相当于三坐标轴，O点为坐标原点。在这个直角坐标体系中，点A到三个投影面的距离便可以用点的三个坐标来表示，如下：

点A到H面的距离Aa=a′a_x=a″a_YW=Oa_z=z坐标

点A到V面的距离Aa′=a″a_z=aa_x=Oa_YW=Oa_YH=Oa_y=y坐标

点A到W面的距离Aa″=a′a_z=aa_YH=Oa_x=x坐标

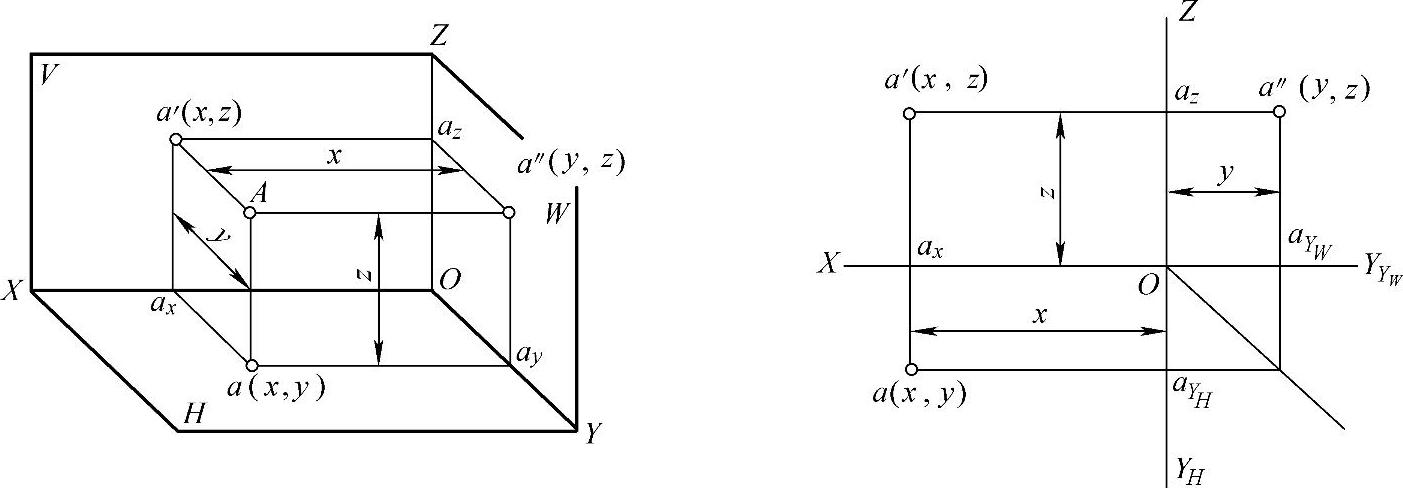
图4-3 点的投影与直角坐标

由此可见，A点的一个投影可以反映A点的两个坐标值。因此，由点的三面投影可以确定其三个坐标值；反之，由点的三个坐标值可以确定该点的三面投影或空间位置。

2.特殊位置点

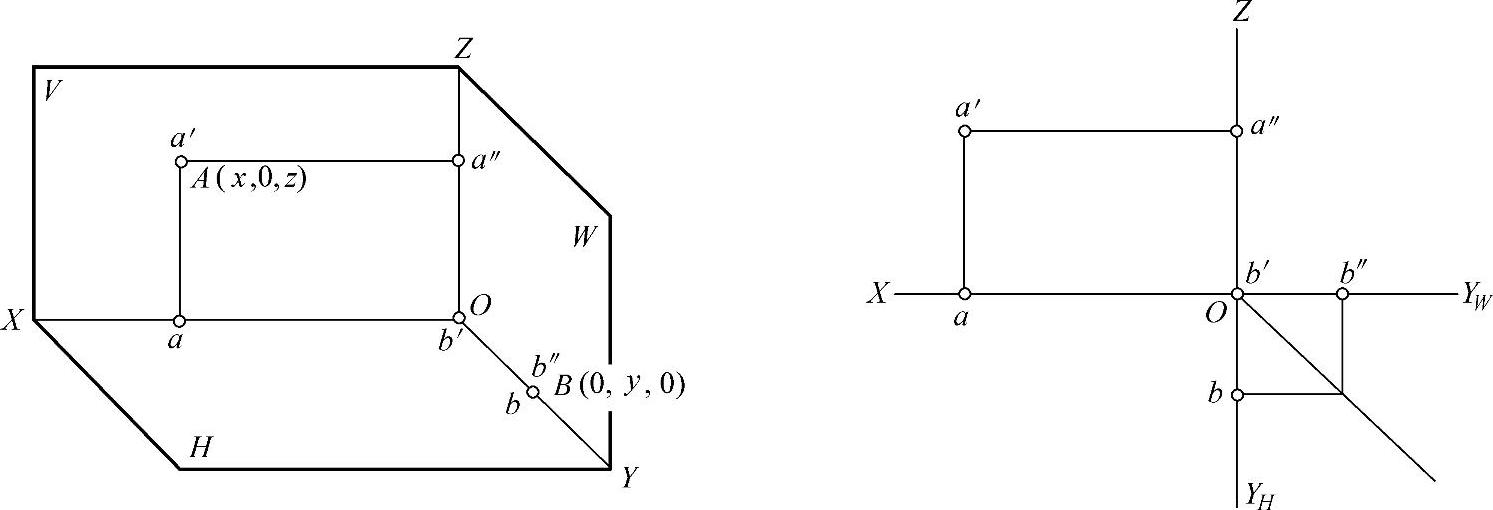
如果空间点处于特殊位置，即某一投影面上的点或某一投影轴上的点，通常称为特殊位置点。如图4-4所示，其投影特性如下：

(www.xing528.com)

图4-4 投影面和投影轴上的点

1）若点在某一投影面上，则与该投影面垂直的轴的坐标必为0。如A点在V面上，则y=0。

2）若点在某一投影轴上，则其他两轴的坐标必为0。如B点在Y轴上，则x=0，z=0。

【实例分析】例4-2 已知A点的坐标为（15，10，20），求作A点的三面投影。

解：作图步骤如图4-5所示。

1）画出投影轴，沿OX轴取Oa_x=15mm，得a_x点。同理，沿OY_H和OY_W轴取Oa_YH=Oa_YW=10mm，得a_YH、a_YW；沿OZ轴取Oa_z=20mm，得a_z。

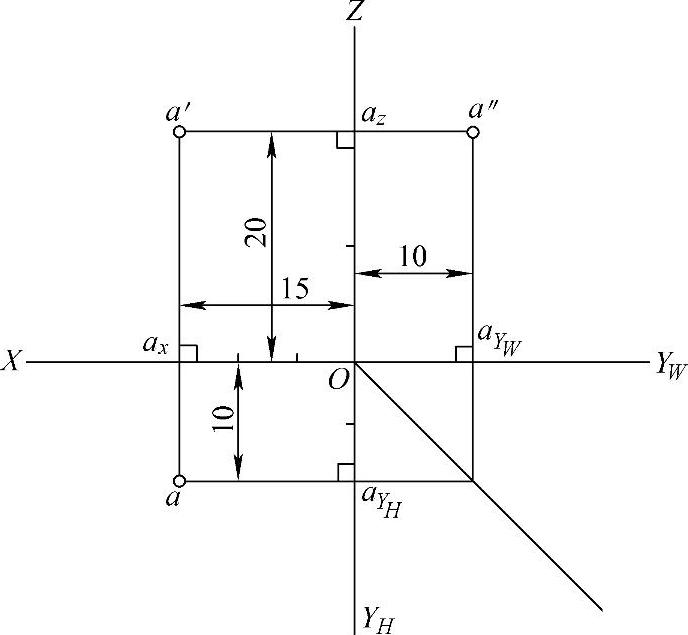
图4-5 由坐标值求三面投影

2）分别过a_x、a_YH、a_YW、a_z四点作OX轴、OY_H轴、OY_W轴、OZ轴的垂线，它们两两相交，交点为a、a′、a″，即为所求点A的三面投影。