【摘要】：图2-31 同心圆法作椭圆a）已知椭圆的长轴AB及短轴CD b）以O为圆心，分别以OA、OC为半径作圆，并将圆十二等分 c）分别过小圆上的等分点作水平线，大圆上的等分点作竖直线，其各对应的交点，即为椭圆上的点，依次相连即可图2-32 四心法作椭圆a）已知椭圆的长短轴AB、CD。
画椭圆的方法比较多，在实际作图中常用的有同心圆法和四心法，同心圆法用于求作比较准确的图形，四心法是一种近似作法，还有一种八点法用于要求不很精确的作图。
1.同心圆法
用同心圆法画椭圆的基本方法是，在确定了椭圆长短轴后，通过作图求得椭圆上的一系列点再将其光滑连接，作图过程如图2-31所示。
2.四心法
四心法是一种近似的作图方法，即采用四段圆弧来代替椭圆曲线，由于作图时应先求出这四段圆弧的圆心，故将此方法称为四心法。作图过程如图2-32所示。
(www.xing528.com)
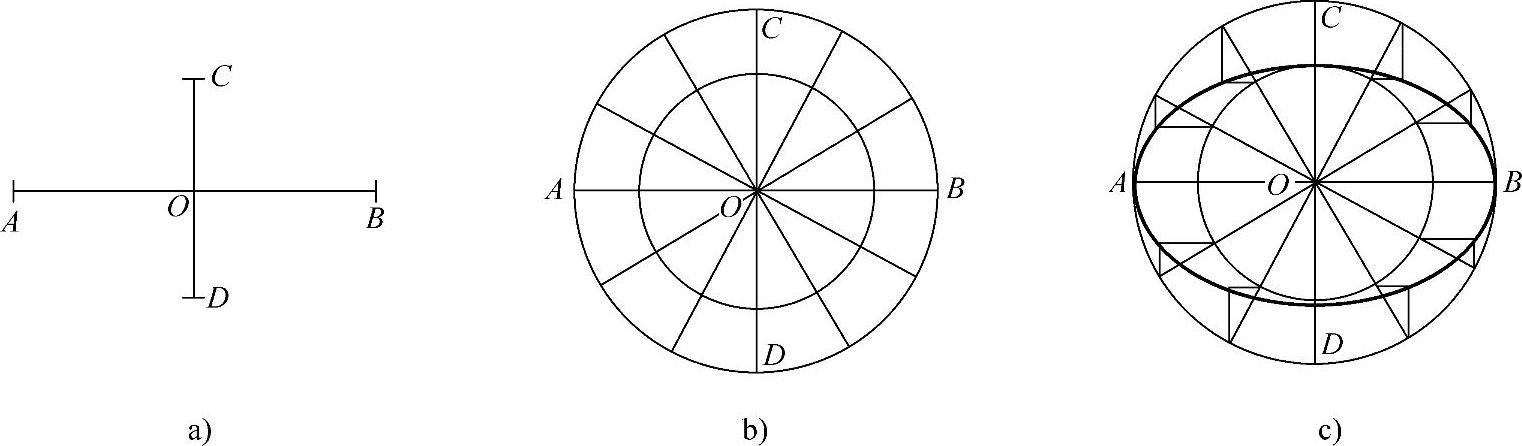
图2-31 同心圆法作椭圆
a）已知椭圆的长轴AB及短轴CD b）以O为圆心，分别以OA、OC为半径作圆，并将圆十二等分 c）分别过小圆上的等分点作水平线，大圆上的等分点作竖直线，其各对应的交点，即为椭圆上的点，依次相连即可
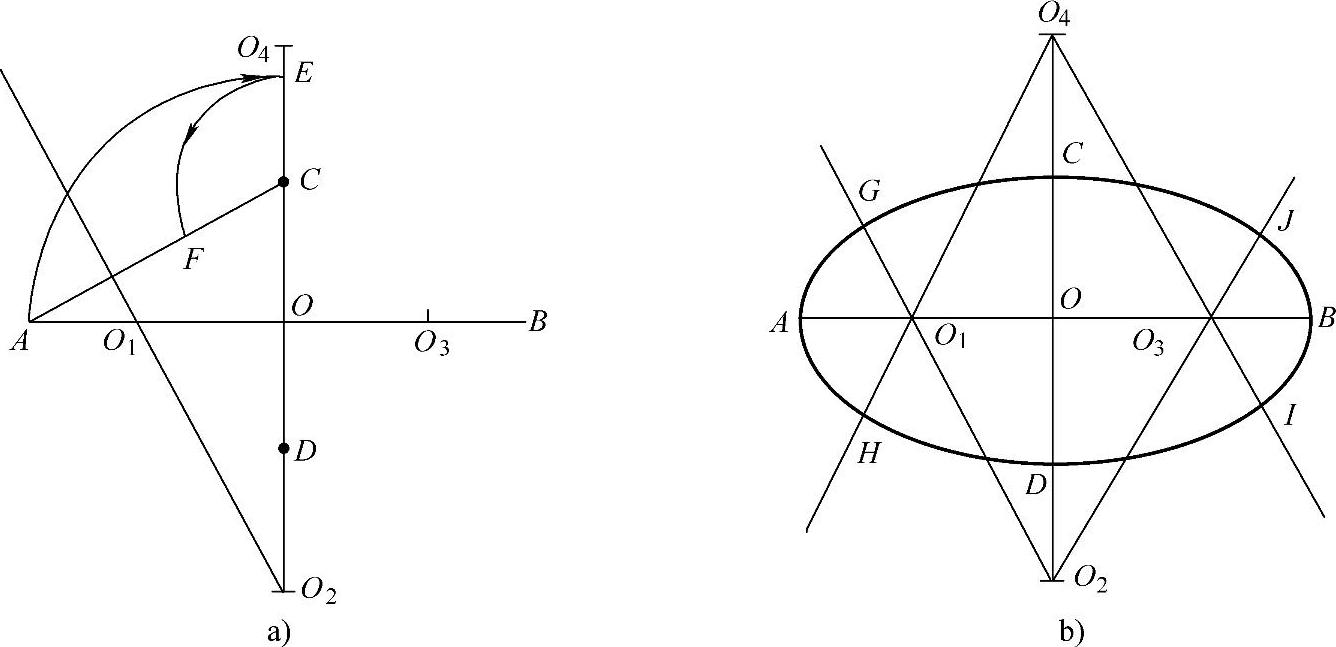
图2-32 四心法作椭圆
a）已知椭圆的长短轴AB、CD。连接AC，以O为圆心，OA为半径作弧交OC的延长线于点E，以C为圆心，CE为半径作弧交AC于点F，作AF的垂直平分线，交长轴于O1，短轴于O2，作OO3=OO1，OO4=OO2 b）连O1O2、O1O4、O2O3、O3O4并延长，分别以O1、O2、O3、O4为圆心，O1A、O3B、O2C、O4D为半径作弧，使各弧相接于G、H、I、J点，即为所求
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
