多轴汽车评定指标及等级限值

（一）单项评定指标

本书采用四个独立的单项评定指标，它们是平均故障间隔里程、平均首次故障里程、固有有效度、故障危害度。

上述四个指标，客观上并非完全独立，而有其相互的内在联系。例如，平均故障间隔里程提高，固有有效度一般就会增大，故障危害度则可能减小。再如，固有有效度和故障危害度之间似乎存在着指数函数关系。除平均故障间隔里程暗含于有效度之中外，其余皆不能互相代替。

此外，我们还给各个单项指标分别规定了零分、不合格、合格、良好、优秀和满分等限值。这些限值虽对整车和发动机整机不起全面评价作用，但它们可以明确在哪一方面存在问题，有多么严重，从而供生产厂家和主管部门参考。下面具体介绍各个单项指标。

1.平均故障间隔里程M_b或者平均故障间隔时间T_b

平均故障间隔里程系整车定程截尾试验的均值M_b，平均故障间隔时间系发动机定时截尾试验的均值T_b，它们分别由下列二式计算：

式中 M_b（T_b）——平均故障间隔里程（时间）[km（h）]；

n——试样汽车（发动机）的台数；

M（T）——试验终止里程（时间）[km（h）]；

r——各试验车辆（发动机）发生的Ⅰ、Ⅱ、Ⅲ类故障的总数。

为供参考，将我军20世纪80年代越野车（发动机）的M_b（T_b）等级限值列于表8-3之中。

表8-3 越野车（发动机）M_b（T_b）等级限值

下面分别说明几个问题：

（1）故障数 故障数有实际的故障数和当量故障数两种。本书采用实际故障数。不采用当量故障数，不仅是当量数难定，而且当量系数算出的数值，实际上是平均当量故障间隔里程（时间），缺乏真实感。当量数值不便和国外同一指标比较，且当量故障数还无法做区间估计。

（2）故障类别的确定 所以不计Ⅳ类故障，一则是因为该类故障对行车安全基本没有影响，但一个故障一个数，它对均值产生很大影响；再则是美军考虑该项指标时，也不计Ⅳ类故障。为方便分析对比，所以只计前三类故障。美军规定，采用随车工具和备件由驾驶人和使用人员在1h内能够排除的任何功能失灵均不认为是故障，这相当于本书规定的Ⅱ类以上的故障。

（3）等级限值得确定 等级限值非常重要，不提限值就等于没提指标。只有通过研究单项指标的等级限值，才能使综合评定分值的等级限值立于可信的基础之上。

在等级限值中，首要的是合格限值。美军提的是最低合格值（Minimum Acceptable Value，MAV）。我们把它当做在试验里程（时间）、子样数和置信度已定的情况下，按在给定的故障数计算的置信下限M_bl（T_bl）。

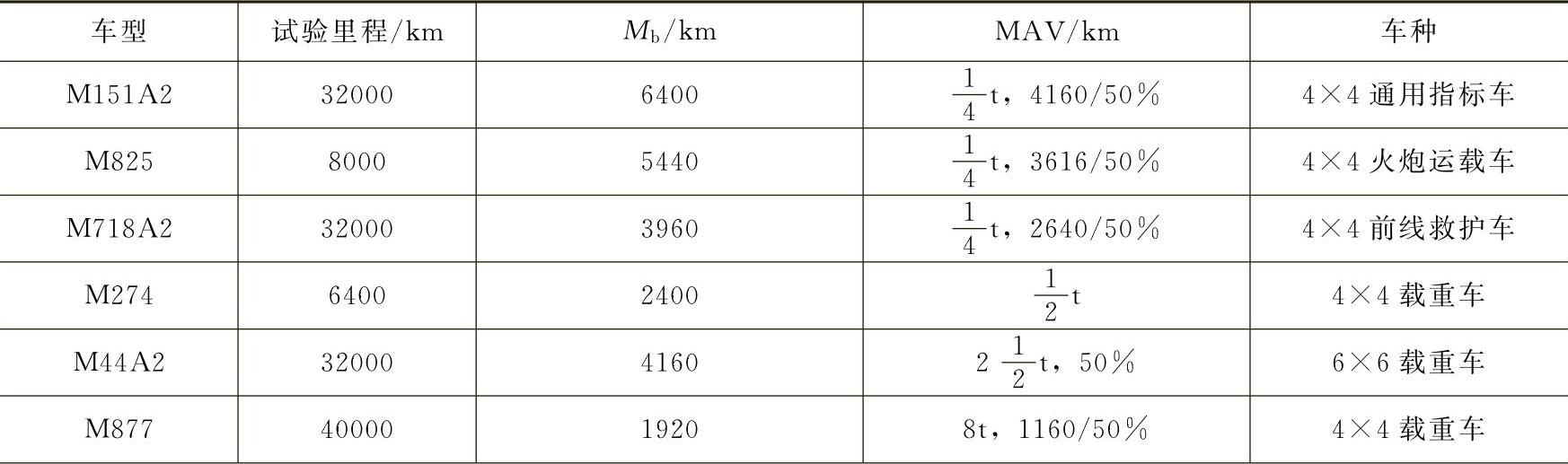
在我国越野汽车可靠性评定办法中，没有直接给出置信下限，而是给出一个合格限值。例如20世纪80年代我国越野车整车的平均故障间隔里程定为1200km。这是衡量M_b值是否合格的一把尺子。然而这把尺子又是怎样制造出来的呢？这主要是根据当时国内越野车的质量水平。我们统计参考了14个车型在2500km和25000km中的试验数据。此外，我们也参考了20世纪80年代美军M系列越野车的技术要求，参见表8-4。

表8-4 美军越野汽车的M_b和M_bl限值

（续）

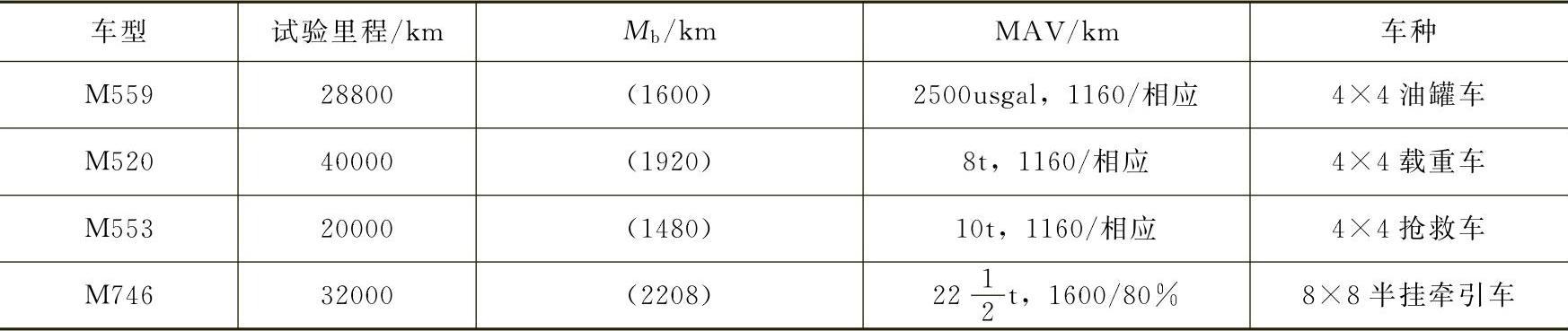
由表8-4的数据可知，表8-3的合格限值，比起美军战术性较强的M151A2等车的MAV值来，显得很低。这除了故障定义之外，主要是美军车辆的质量较高。表8-3的限值只相当于或略高于美军战术性较差的特种车和越野载货车的MAV值，为1160km。

我军当时越野车1200km这个合格限值，是按试验里程M=2500km，子样数n=2，置信度1-α=0.5的情况下，规定每台车允许出现1.75个不分类别的Ⅲ类以上故障的条件，利用式（8-8），计算出平均间隔故障里程的限值M_bl来。

式中 χ²——卡方表数值；

r——三类以上故障数；

α——显著性水平，或区间之外的概率；

（1-α）——置信度，也就是预定的概率。

代入上述数据，可得

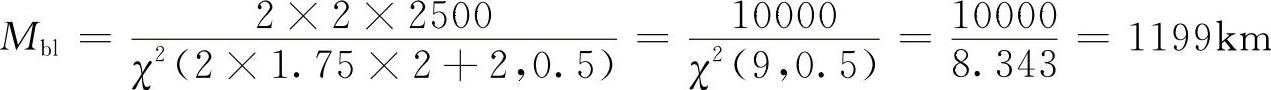
那么，1.75个故障又是如何确定的呢？这是根据美军车辆的试验里程M和最低合格限值MAV，再假定子样数n=2，置信度（1-α）=0.5，来分析他们的单车故障数r并换算到2500km的故障数r'来确定的。

在已知平均故障间隔里程的限值M_bl后，可用下式近似估算单车故障数：

利用式（8-9）换算的美军部分越野车单车故障限值列于表8-5中。

表8-5 美军部分越野车单车故障限值

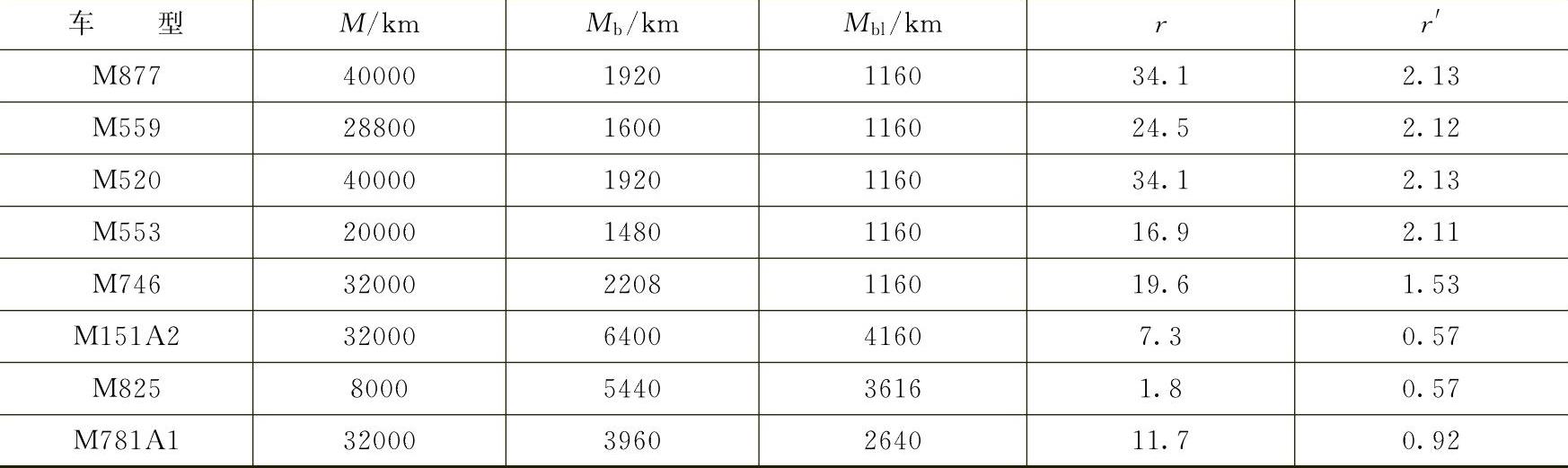
由表8-5数据可知，美军换算为2500km试验的单车故障数，特种车和载重车平均为2个。考虑到他们的故障数定义较高，加之试验里程高，所以当时我军越野车定为1.75个。在2500km试验中，按照美军的限值，相当于我军的单车故障数为20个左右。

发动机的及格限值，汽油机定为60h，柴油机定为90h，这是和整车对比确定的。如果把整车的1200km作为1倍看待的话，在假设平均技术车速，汽油机车辆为50km/h，柴油机车辆为40km/h以下，那么，汽油机车辆为60×50÷1200=2.5倍，柴油机车辆为90×40÷1200=3倍。至于其他限值，则是按合格为60分以上，良好为80分以上，优秀为90分以上，满分为100分，且给定100分时的里程或时间的上界，然后按等比的关系示出的。

2.平均首次故障里程M_f或平均首次故障时间T_f

平均首次故障里程系整车定程截尾试验的估计值M_f，平均首次故障时间系发动机定时截尾试验的估计值T_f，它们分别由下列二式计算。

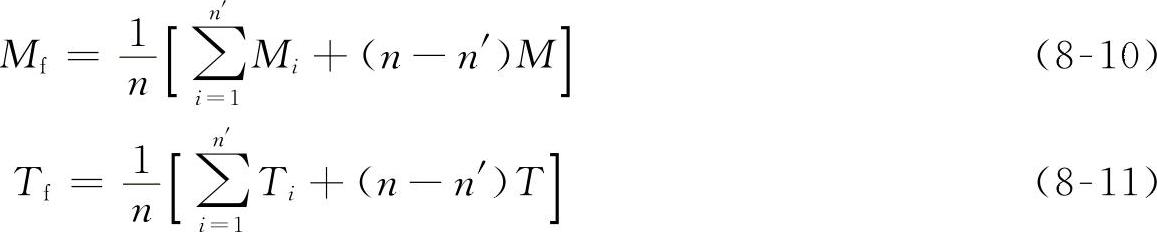
式中 M_f（T_f）——平均首次故障里程（时间）[km（h）]；

n——试验车辆（发动机）的台数；

n'——发生故障的车辆（发动机）的台数；

M_i（T_i）——发生故障的车辆（发动机）的首次故障里程（时间），[km（h）]；

M（T）——试验截止里程（时间）[km（h）]。

为供参考，现将我军20世纪80年代的越野车和发动机的平均首次故障里程（时间）M_f（T_f）的等级限值列入表8-6中。

表8-6 M_f（T_f）的等级限值

平均首次故障里程（时间）这个指标，一般用以评价损坏后不可修复的一次性使用产品，它也叫做平均寿命。汽车是可修复产品，似乎不应提这个指标，美军也没提这个指标。越野汽车“蓝皮书”所以强调这个指标，是根据我国汽车工业当时的实际情况，希望用这一指标来推动装配调整质量，改变那种新车一出门就走不动的现象。注意，M_f（T_f）是不计Ⅳ类故障的，因它不影响行车安全，且一般不需停车。

3.固有有效度A_i

有效度A是产品使用效率和工作能力的标志，它和运行完好率是同一概念。而固有有效度A_i则是指产品本身所具有的工作效能。有效度是指总工作时间与总修复时间及总工作时间之和的比值。亦即

式中 MTBF——平均故障间隔时间，亦即总工作时间；

MTTR——平均故障修复时间，亦即总修复时间。

式（8-12）还可表为如下形式，即

式中 MR—维修系数。

维修系数就是总修复工时与总工作小时数之比，亦即

式中 n——被试样车或样机总数；

T_oi——第i台样车（样机）的工作总时间（h）；

T_ri——第i台样车（样机）排除故障的总时间（h）。

排除故障总时间是指各类故障的诊断、修理和验证时间，不包括例行保养维修时间以及事故和行政等时间。

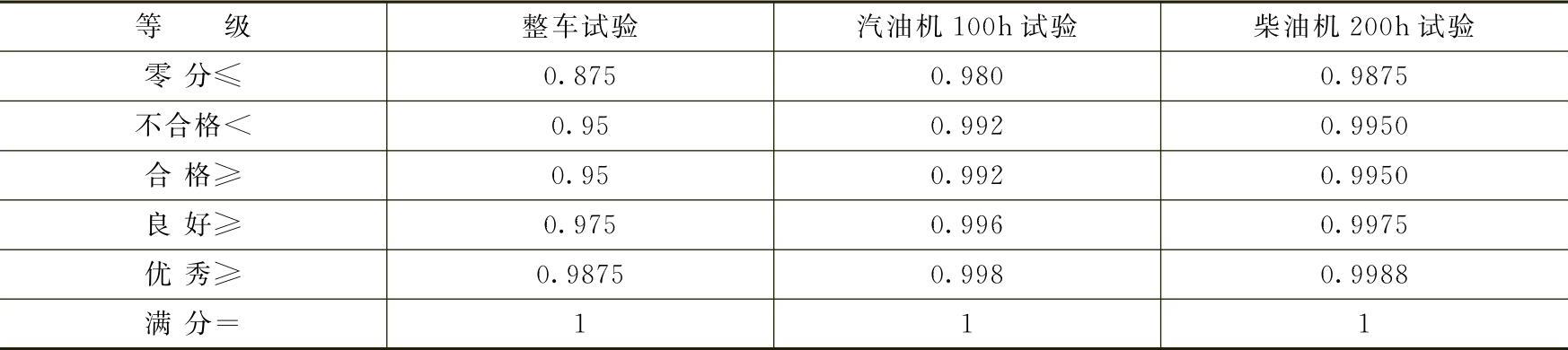
由式（8-13）和式（8-14）可知，固有有效度就是维修系数的标志。为供参考，现将我军20世纪80年代军用越野汽车（发动机）固有有效度A_i的限值列入表8-7之中。

表8-7 A_i的等级限值

有效度指标，按说是不应放入可靠性考虑的，美军只是把它放入维修性中来提的。我们所以把它放入可靠性中，一是因为维修性和可靠性不可截然分开，二是我军当时还没有单独提要求。美军把导致停驶，产生致命或灾难性以及采用随军器材设备（OEM）在1h内不能排除的功能失灵定义为可靠性的故障，而对我们所指的Ⅳ类故障是不予计算的。然而，在维修性中，Ⅳ类故障却是应予考虑的。有效度这个指标的作用，在很大程度上是要防止“三天打鱼，两天晒网”的小毛病不断的现象。因此，在把有效度作为单项指标看时，应理解为维修性和工作效率的标志。但在进入综合评价时，它又在一定程度上反映着可靠性的水平。

第i台样本（样机）的工作总时间T_oi，是指各试验产品的试验运行或工作（Operation）时间，即平均无故障工作时间（MTBF）。一律用时间表示，是因为修理只能按工时统计。至于整车，当然也可用各试验样车的试验里程，然后，以平均技术速度换算为工时。

排除故障总时间T_ri，是指各试验产品在试验过程中的实际修复时间，即计划之外的维修时间。不计驾驶人日常的检查维护时间，更不计事故和候件等行政时间。事故是外因，行政时间仅仅反映组织管理水平，不反映产品的固有属性。这正是固有有效度的含义。

此处所讲的维修时间，在美国军用汽车标准中叫做平均修复时间（Mean manhours to perform a corrective maintenance action），其中corrective maintenance是改正维修之意，显然是计划之外的，包括故障后驾驶人的修理，而不是计划之内的预防性维修（Preventive Maintenance）。只有这样定义维修时间，有效度的最大值在理论上才有可能达到1。

表8-7中A_i的限值是如何确定的呢？作为整车来说，是在参考国内外越野车的要求和试验结果的情况下，经过分析确定的。

在当时，国内车辆试验，由于缺乏经验，故障统计尚不严密，因此算出的有效度可能偏高。当时8个车型在2500km试验中A_i的平均值为0.94。

美军战术性较强的小吨位车型，一般不提有效度这个指标，而是提维修总工时和维修系数，参见表8-8。他们的维修总工时，包括计划内的维修工时和计划外的修复工时。美军对于大吨位的、短途使用的变型车，则是按使用情况进行任务（Mission）试验，故还有平均任务试验故障间隔里程的提法（Mean Miles Between Mission Failure MMBMF）。对这类车的维修性提了如下8个指标。

1）驾驶人的平均维护工时T_dm。

2）驾驶人的最高修复工时T_dr。

3）总维修工时与总工作小时之比MR_g。

4）分队维修总工时与总工作小时之比MR_tm。

5）总修复工时与总工作小时之比MR_r。

6）平均修复时间MTTR。

7）固有有效度A_i。

8）平均无故障工作时间MTBF。

表8-8 美军10个车型的总维修工时、维修系数及有效度

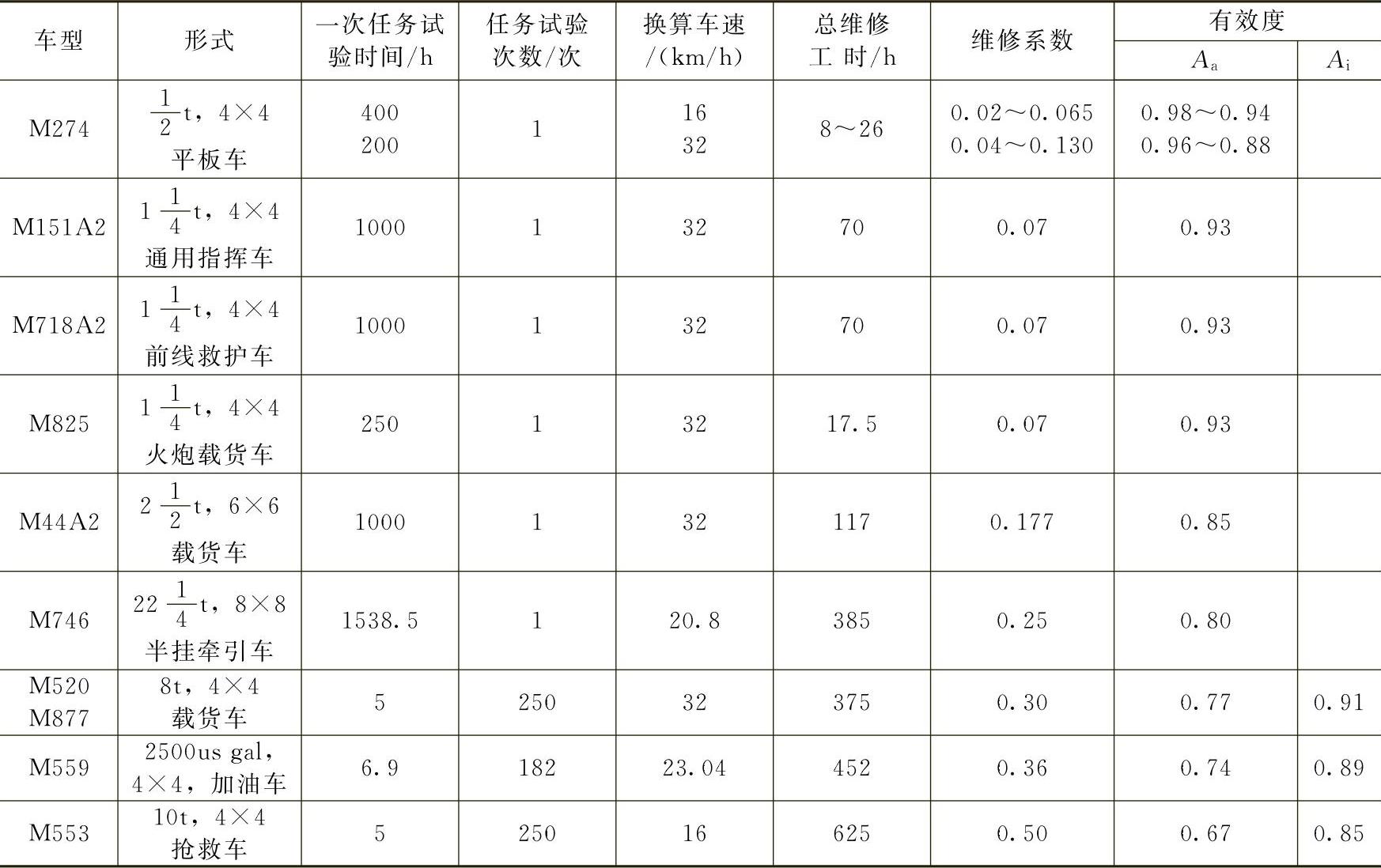
此处，MTBF中的故障有别于MMBMF中的故障。前者相当于我们定义的各类故障，后者比Ⅲ类故障还略为严重。

美军4个车型的8个维修性指标列入表8-9之中。

表8-9 美军4个车型的8个维修性指标

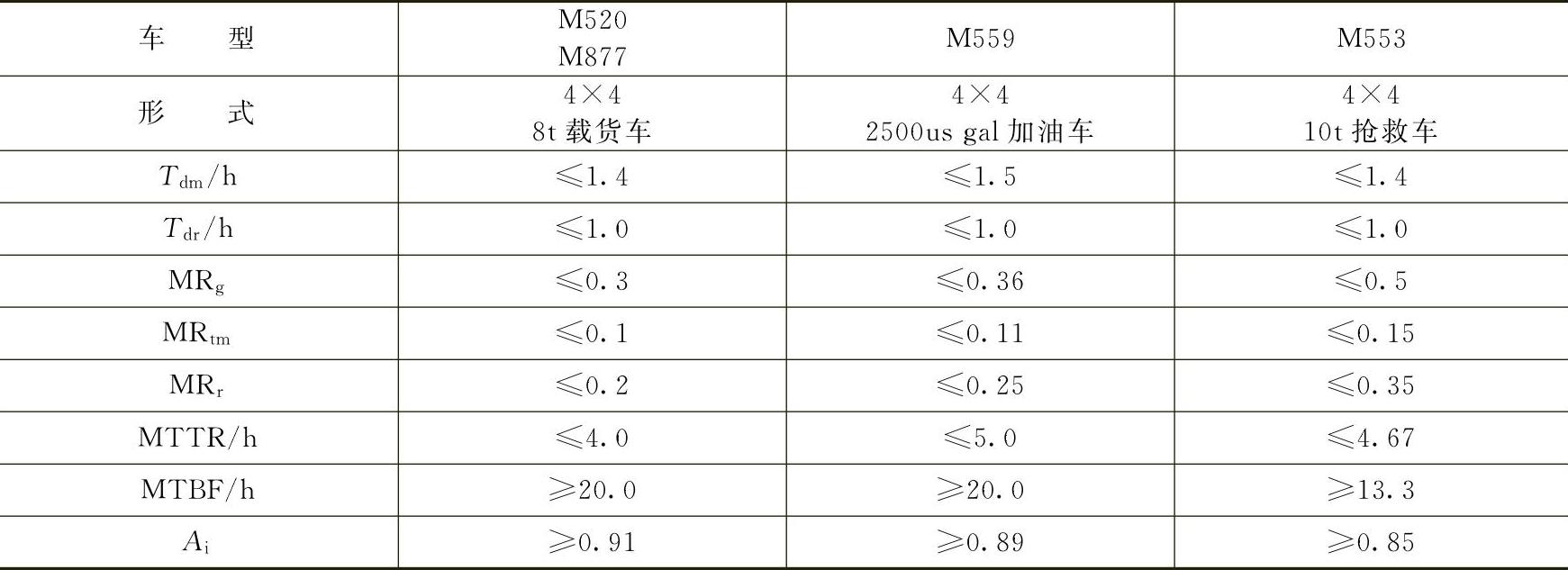
由表8-8数据可知，表8-7中的0.95这个A_i的合格限值略高于美军作任务试验的M520等车型的限值。但比M151A2等车型的要求要低一个等级。这些车型在考虑计划内维修的情况下，我们当时所提的限值才与之接近。

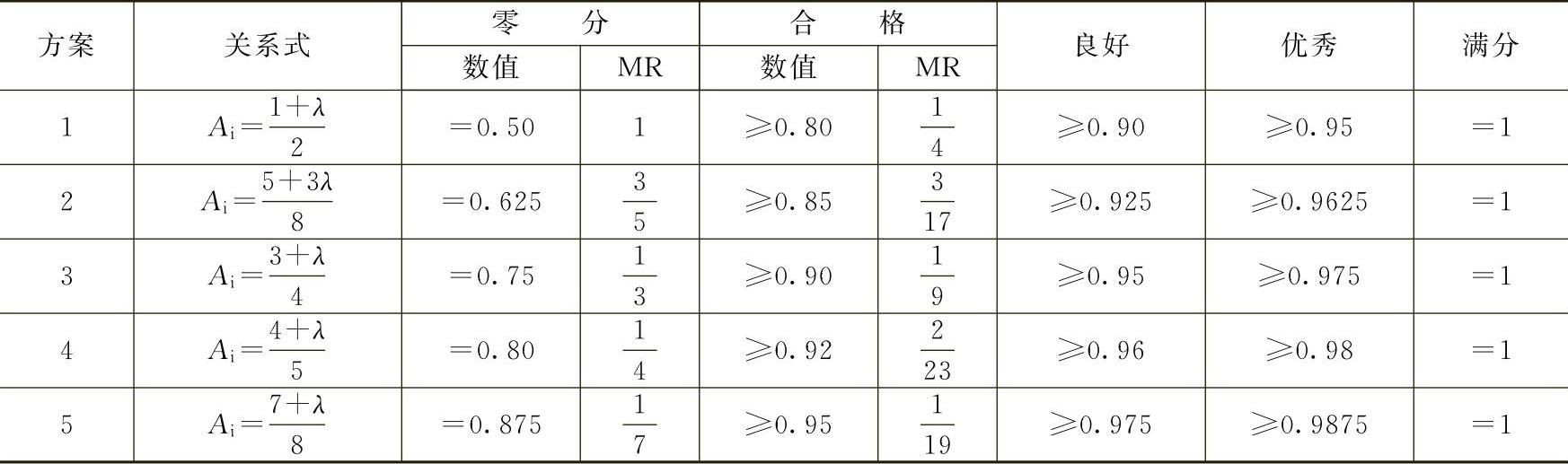
为分析确定固有有效度A_i值，当时提了（0.80、0.85、0.90、0.92、0.95）五个对比方案，并以λ作横坐标，A_i作纵坐标分别建立了A_i和λ的关系式：A_i=f（λ），以此关系式算出了各方案的各级限值，并对比列于表8-10之中。

表8-10中的零分和合格栏目下，列有维修系数MR，它正是我们选定方案的依据。表中的第4方案，A_i值的变化范围是0.8～1.0。下限是说，只要修复时间占了工作时间的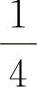就为零分。合格限值告诉我们，修复时间若占了工作时间的，也就不合格了。若把0.95作为A_i的合格限值，修复时间大于工作时间的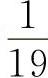就不合格，这就有点过严了。

附带说明一下，关系式A_i=f（λ）不仅可以求出各分位点λ的A_i值，而且可由此找出它的反函数λ=F（A_i）。以后将看到这个反函数便是建立综合分值公式的有效度这一因素的系数式。

表8-10 固有有效度A_i的限值方案

作为发动机，A_i的限值主要是参考当时JB 3744—1984《汽车发动机可靠性试验方法》的要求来决定的。该标准规定Ⅰ类发动机300h，Ⅱ类发动机600h，故障停车不得超过8次。Ⅲ类以上发动机每小时故障停车不应超过1次。排除故障时间应在20min以内。

Ⅰ类发动机用于总重在2.5t以下的汽车，这显然是汽油机。

Ⅱ类发动机用于总重在2.5～6t范围内的汽车，这绝大部分是汽油机。

Ⅲ类以上发动机大部分是柴油机，由此可分别计算出它们的维修系数及其有效度。

Ⅰ类（汽）：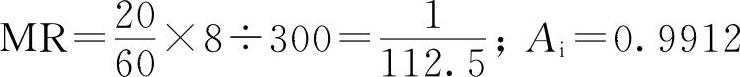

Ⅱ类（汽、柴）：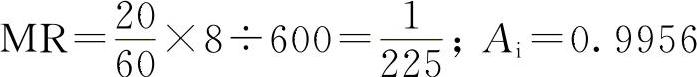

Ⅲ类（柴）：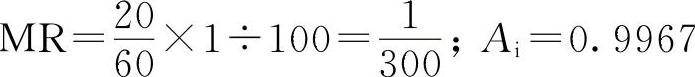

由此可知，汽油机A_i的合格限值定为0.992（MR=1/124），柴油机定为0.995（MR=1/199），还是一个低标准，是放得较松的。

4.故障危害度H

故障危害度就是各类故障的综合危害程度。故障有大有小，有轻有重。如果只把各类故障数的简单和作为评价指标，那就没有反映出故障的性质和严重程度来。为了相对合理地表达各类故障的差异和影响，故给各类故障一个相应的危害系数（权系数）ε_i。这个系数与全部试验车辆或发动机的各类故障数r_i的积，便是第i类故障的危害度。综合各类故障的危害度并取其均值，便得到参试车辆或发动机平均故障危害度的计算公式了：

式中 H——故障危害度，其最大数值，由表8-11限定；

n——参试样车或发动机的总数；

r_i——各样车或样机第i类故障总数；

ε_i——各样车或样机第i类故障的危害系数，其数值如下：(www.xing528.com)

致命故障ε₁=1000严重故障ε₂=40

一般故障ε₃=5轻微故障ε₄=2

故障危害度的等级限值列入表8-12之中。

表8-11 故障危害度H的最高限定值

表8-12 故障危害度H的等级限值

（续）

我军的危害系数与美军较为接近，美军ε₁=1000，ε₂=40，ε₃=20/3。ε₂取为40，在整车2500km试验中，正好是一台车的合格限，即只允许出现一个二类故障。

之所以要把危害度作为一个单项指标提出，是考虑到这一指标具有可靠性的本质特色。仅这一指标的高低，就在相当程度上反映出可靠性的优劣。

故障危害度等级限值的确定，除参考20世纪80年代美军和我军越野汽车和发动机的实际水平外，还从故障的角度来确定合格限值。

例如整车2500km试验，1台车仅允许出1个Ⅱ类故障，或8个Ⅲ类故障，或20个Ⅳ类故障。注意说是允许出一个Ⅱ类故障，实际上是不允许，因为在此同时，完全有可能出Ⅲ类和Ⅳ类故障。由此可知，这个合格限值也不是太松的。1个Ⅱ类故障，在整车2500km试验中，对一台车来说是合格限，对两台车来说正好是良好限。在整车25000km试验中，一台车仅允许出10个Ⅱ类故障，80个Ⅲ类故障，200个Ⅳ类故障。但须注意，在任何试验中，绝不允许发生Ⅰ类故障，只要出现一个Ⅰ类故障，不管子样数n为多少，都认为得零分。

除合格限值外，其他限值都是以满分H=0按等比关系确定的。

发动机的合格限值，则是以整车2500km试验仅允许出一个Ⅱ类故障为基础，并假设汽油机车辆的速度为50km/h，柴油机车辆的速度为40km/h，再按里程或故障数的要求来计算出来的。

1）按里程数的要求。允许出一个Ⅱ类故障，整车运行2500km，要求汽油机运转小时数的换算里程应为10000km，柴油机运转小时数的换算里程应为20000km。于是，

汽油机的合格限值为

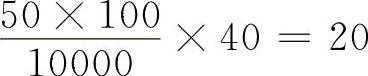
柴油机的合格限值为

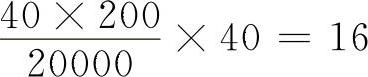
2）按故障数的要求。换算里程同为2500km，整车允许出一个Ⅱ类故障，汽油机允许出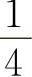个Ⅱ类故障（或2个Ⅲ类故障），柴油机允许出个Ⅱ类故障（或1个Ⅲ类故障），于是，

汽油机的合格限值为

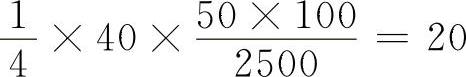
柴油机的合格限值为

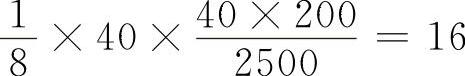
至于其他限值，仍是以满分时的H=0，然后按等比关系确定的。

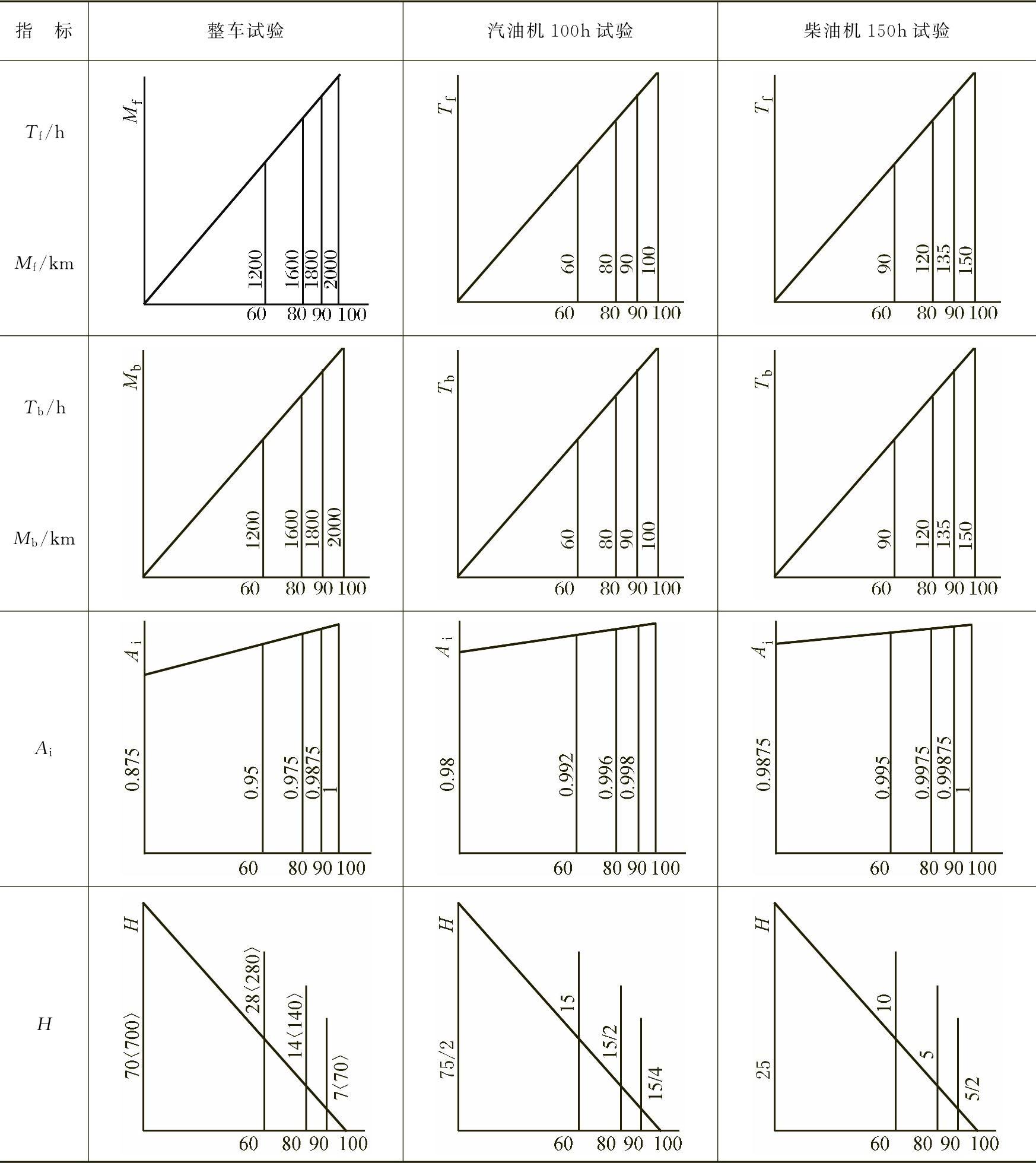
为便于查找和给人以直观的印象，特将4个单项指标的各级限值绘成图样排列于表8-13之中。

表8-13 各单项指标的各级限值

（二）综合评定分值

1.公式的建立

综合评定分值是由平均首次故障时间（里程）T_f、平均故障间隔时间（里程）T_b、固有有效度A_i以及故障危害度H四个单项指标组成的一个综合评定指标，是被试产品可靠性水平的全面标志。

综合评定分值用下式计算：

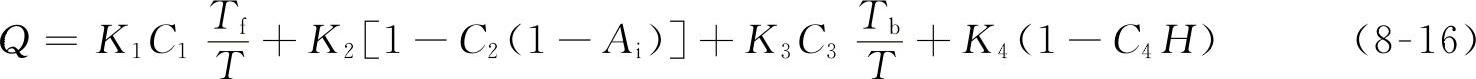
式中 Q——综合评定分值（分）；

T——试验截止时间（里程）[h（km）]；

T_f——平均首次故障时间（里程）[h（km）]；

A_i——固有有效度；

T_b——平均故障间隔时间（里程）[h（km）]；

H——故障危害故；

K₁、K₂、K₃、K₄——分别为T_f、A_i、T_b和H的权系数；

C_i——试验类型系数。

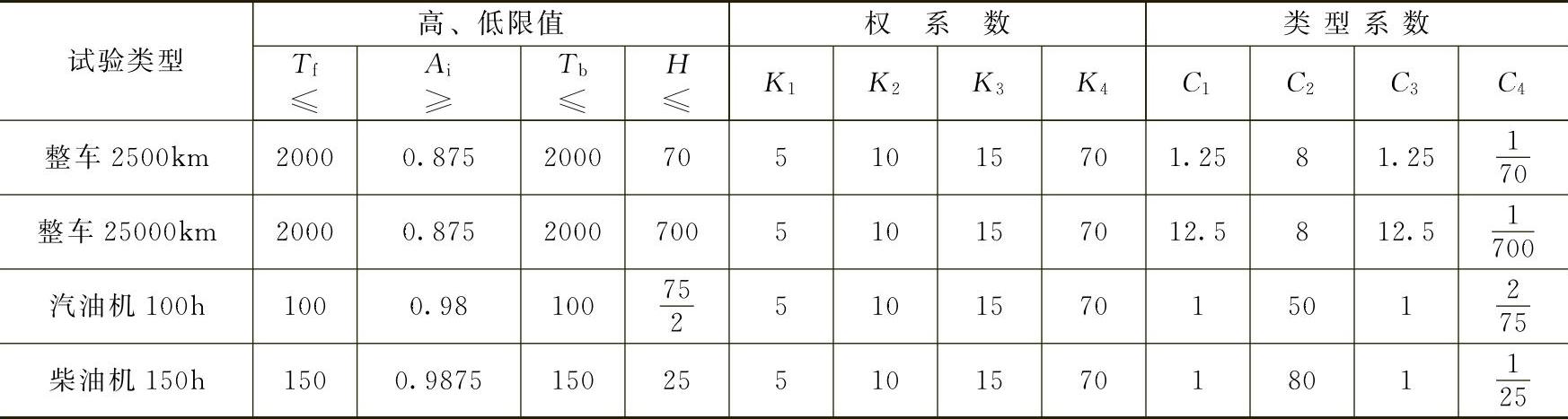
T_f、A_i、T_b和H的高低限值、权系数以及试验类型系数暂按表8-14的数据取值。今后，随着汽车质量水平的变化，随时可以修订。

将表8-14中的系数代入前式，便得到下列简化计算公式：

整车2500km试验：

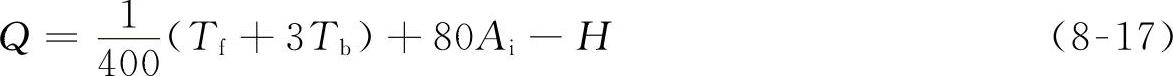
整车25000km试验：

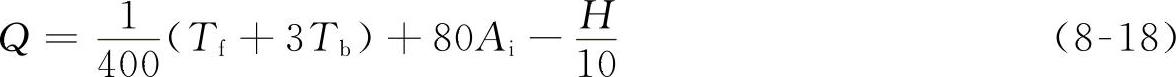
汽油机100h试验：

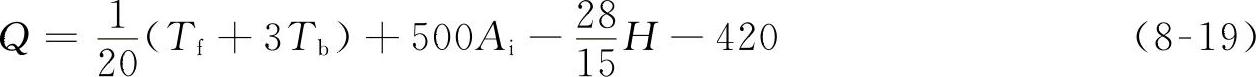
柴油机150h试验：

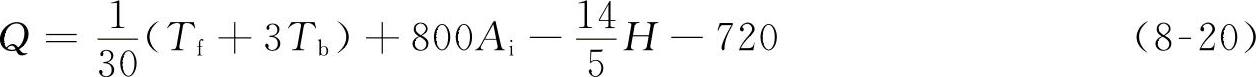
注意：当单项指标的测试值超出高、低限值时，须按所给限值计算。

表8-14 单项指标的高低限值及系数

综合评定分值的等级限值列入表8-15。

表8-15 Q值的等级限值

下面就Q值公式的结构特点、结构设计、各种系数和限值的确定以及可行性等问题作一个介绍。

2.公式的结构特点

Q值公式的结构特点是线性组合。即先把4个单项指标T_f、A_i、T_b和H分别设计成单项指标因式X_i，再给各因式一个权系数K_i，最后把它们加起来便构成了我们的综合分值公式Q=∑K_iX_i。单项指标因式分别是C₁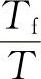、[1-C₂（1-A_i）]、C₃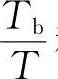和（1-C₄H）。各因式均无量纲，各单项指标在因式中以一次方出现。因此，各因式均是在0～1之间保持线性变化的关系。例如有效度因式，当A_i=1时，[1-C₂（1-1）]=1；当在整车2500km试验中，A_i取下限值0.875时，[1-8×（1-0.875）]=0。加之∑K_i=100，所以，Q值总是在0～100之间保持线性变化。

因此，Q值公式概念清晰，形式简明。

3.公式的结构设计

加权处理，线性组合是这一公式的结构特点，也是结构设计的中心内容。但此处所要介绍的是单项指标因式的设计。

因式设计的基本想法是：在以各单项指标y为纵坐标，以单项指标因式x为横坐标的坐标系（图8-4）中，建立一个直线方程x=F（y、C），并保证x无因次。式中的C为试验类型系数，C=f（y_a），y_a是各单项指标的合格限值。

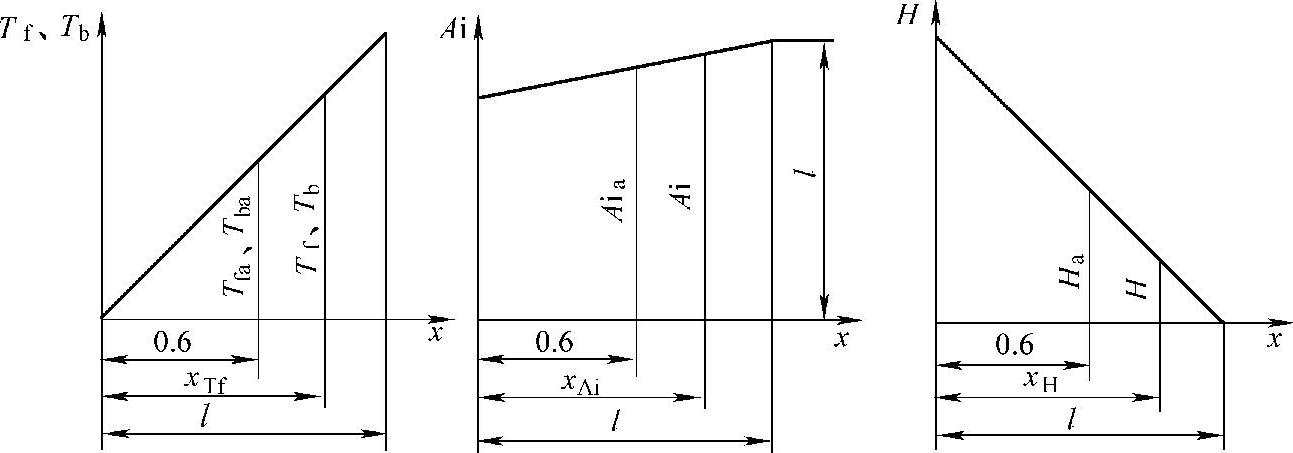
图8-4 横坐标与单项指标的关系

这样，只要给定了单项指标的合格限值y_a，试验类型系数C就被确定了。一旦确定了C，再得到了单项指标的测试值y，那么该指标应得分值的坐标x就被确定了。x乘以权系数K，就得到了该指标的分值。

1）求T_f（T_b）因式x_Tf（x_Tb）。由图8-4可得

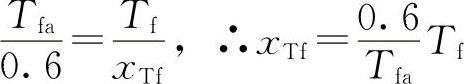
为保证试验类型系数为无因次系数，我们可引进试验总时间T来把前式变成如下形式：

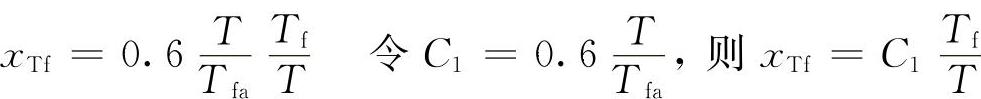
同理，

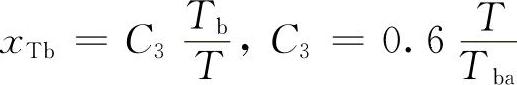
2）求A_i因式x_Ai。根据图8-4有

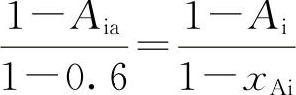，解之可得

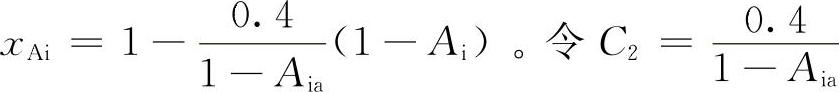，则有

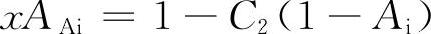
3）求H因式X_H。按图8-4有

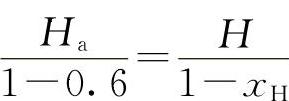，解之可得x_H=1-，

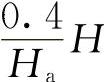令C₄=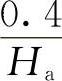，则x_H=1-C₄H。

H因式我们可以这样来理解它：C₄H是危害度，而（1-C₄H）便是“无害度”。值得注意的是，（1-C₄H）还正好是指数函数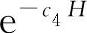展开式的前两项。

由上述可知，Q值公式结构严谨，依据充分。

4.确定单项指标的高、低限值

单项指标高、低限值的作用，在于控制单项指标因式在0～1之间变化，亦即控制综合评定分值Q在0～100之间变化。否则就有可能使Q值大于100或得负数。

1）确定最低限值。T_f、T_b的最低限值就是零，而A_i不到零，H不无限增大时就应得零分。确定得零分的最低限值，可令单项指标因式为零，并代入试验类型系数便可求出。例如求整车2500km试验A_i的最低限值A_il，可令1-C₂（1-A_i）=0，因C₂=8，所以

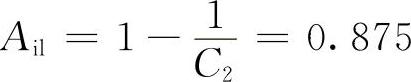
2）确定最高限值。单项指标获得满分时的值就是最高限值。很明显，A_i=1，H=0就获得满分，然而T_f、T_b并不需要达到试验总里程才得满分。确定它们得满分的最高限值，可令单项指标因式为1，并代入试验类型数便可求出。例如求整车2500km试验T_f的最高限值T_fu，可令C₁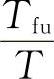=1，因C₁=1.25，T=2500km，所以

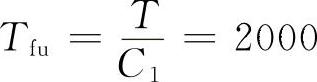
5.确定试验类型系数和权系数

为使Q值公式具有普遍的意义和广泛的适应性，故式中含有4个试验类型系数和4个权系数。这些系数的数值，既反映了产品的质量水平，也体现出主管部门的政策要求，因此，它们是这一公式的灵魂所在。

1）确定试验类型系数。试验类型系数，既是区别不同里程的整车试验、各种发动机试验或者其他总成部件试验的一个系数，也是合格限值的标志。在各单项指标合格限值已定的情况下，可按下列公式分别计算T_f、A_i、T_b和H的试验类型系数：

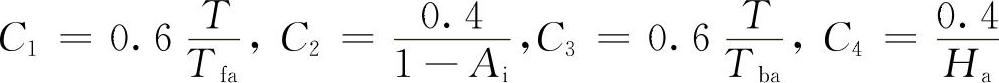
上列公式，还可通过令各项指标因式等于0.6而得到。

2）确定权系数。权系数是各单项指标在综合分值公式中的地位表现，更是质量管理政策的体现。因此，可根据主管当局的具体政策确定各单项指标的权系数。

例如，总后车船部和中汽公司质管部规定：在整车2500km试验中，平均1台车不得发生1个Ⅱ类故障。亦即当发生1个Ⅱ类故障时，应满足Q＜60分。据此，就可确定故障危害度的权系数K₄了。

令Q值公式的前3项得满分（事实上，只要一有故障发生，有效度就不能得满分，Q值就不能得60分），由于∑K_i=100，前3项得满分就是（100-K₄），于是得到下面的关系式：[（100-K₄）+K₄（1-C₄H）]≤60。我们已知C₄=1/70，Ⅱ类故障的危害系数是40。将其代入后便可解得K₄≥70。为了既能满足政策要求，又不致过分降低其余3项指标的分值故取K₄=70。

前3项权系数的和30这个数字又怎样分配呢？同样应由政策确定。美军把平均故障间隔里程看得较重，有效度本属维修指标，加之我们的平均首次故障里程合格限值提得较高，综合权衡这些因素，故取K₁=5，K₂=10，K₃=15。

上述系数的确定过程让我们清楚地看到：Q值公式具有相当的灵活性和适应性。它既适应于不同的试验类型，也适应于产品质量水平的变化和政策的改变。不管怎么变，都不需要改变公式本身，只需调整系数就可以了。

6.公式的可行性

Q值公式的可行性可从理论上、特例分析上以及实际计算上来考核。

从理论上说，在Q=f（T_f、A_i、T_b、H）的关系式中，Q值总是和T_f、A_i、T_b和H保持着线性的关系。若各单项指标因式分别为0、0.6和1，那么Q值必然相应地得0分、60分和100分。亦即Q值和各单项指标具有一致变化性。若各单项指标因式并非同时取得某一数值，那么权系数就发生作用了。所以，只要各项指标的限值和权系数定得合理，那么Q值就相对合理了。

理论与政策，科学性和实用性应有机地结合。例如，故障危害度因式，有人主张采用函数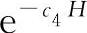。理由是较为科学，符合故障规律。我们认为：汽车可靠度与故障的关系未必就是指数分布；由于采用了当量故障形式，也不符合自然故障分布规律；再退一步，还算其符合，那在Q值整体公式中，前3项是线性函数，加上第4项指数函数又是什么分布呢？我们采用（1-C₄H）的形式，既保证了整个公式的线性化，形式鲜明，计算简便，又是指数函数的工程简化。更重要的是纯指数函数，只有当故障趋于无穷时，才得零分，而（1-C₄H）仅当故障达到某一数值时，就得零分。所以，Q值公式，既强调了政策性的实用，也注意了它的依据性。

特例分析：我们分别以汽油车辆2500km试验和汽油机100h试验为例进行计算分析，并假定子样数n=1，修复时间1个Ⅲ类故障为0.5h，Ⅳ类故障为1/12h，换算车速为50km/h。故障发生的时刻都以试验开始和结束的一瞬间计算。不同情况下所计算的结果列入表8-16。

由表8-16可知：整车2500km试验，平均每一台车若在最后一瞬间发生1个Ⅱ类故障恰为合格（事实上有了Ⅱ类故障不会合格，因不可能恰好在最后一刹那发生Ⅱ类故障）；若在开始瞬间发生1个Ⅲ类故障，就得不到优秀；若在开始瞬间发生2个Ⅲ类故障就得不到良好，若在最后瞬间发生2个Ⅲ类故障恰为优秀（实际不可能）；若在最后瞬间发生1个Ⅳ类故障就不能得满分。

表8-16 特例计算结果

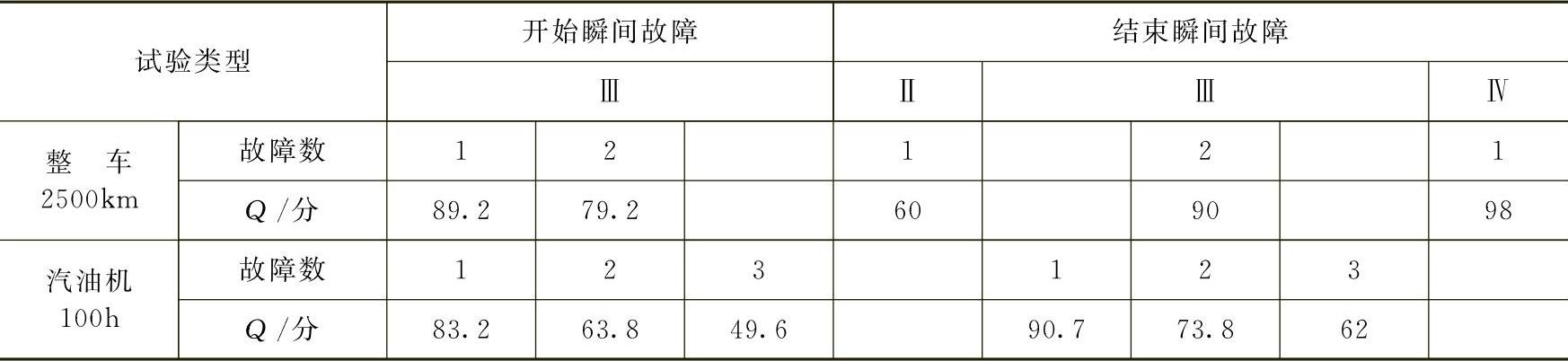
汽油机100h试验平均每台发动机若在开始瞬间发生1个Ⅲ类故障还可得到良好；若在开始瞬间发生2个Ⅲ类故障还将合格；若在结束瞬间发生1个Ⅲ类故障能够勉强得到优秀；若在结束瞬间发生3个Ⅲ类故障只能勉强合格等。

从上述典型例子的分析来看，Q值公式还是经得起推敲的，不致越格。

总之，Q值公式形式简明，结构严谨，且具有广泛的适应性，故可作为一把度量我国越野汽车可靠性的尺子。然而，这一公式也并非完美无缺。例如，采取加权的办法把4个独立的单项指标强行组合在一起，还缺乏更多的科学根据；各指标的合格限值及其权系数也未必定得合理。我们仅是从无到有地迈出了第一步，故还有待于通过今后的实践，使之合理完善。