多轴汽车-可靠度函数及其定量指标

任何产品都可按一定的试验方法鉴定它们的可靠性或者比较它们的可靠性。可靠性不只是定性的描述，而且可以是定量的描述。产品从开始使用到某一时刻这段时间内，维持规定功能的能力可用可靠度R（t）这个指标来表示。

所谓可靠度，就是产品无故障的概率，或者说产品从开始使用到某一时刻这段时间内，产品维持规定功能的能力。也就是产品在规定的条件下和规定的时间内完成规定功能的概率。所谓概率系指在一定条件下，一个随机事件发生的可能性的大小。它是一个在0～1之间的数值，可用百分比表示。可靠度越大，说明产品越可靠。它是可靠性的一个定量指标。

假如一辆汽车在运行500h的可靠度为99%，那么这就意味着如果多次抽取100辆同样的汽车在规定的条件下工作500h，平均有99辆能够完成其规定的功能。与可靠度相对应的是不可靠度F（t），它也称为累计故障率。可靠度R（t）与不可靠度F（t）之和等于1，即

如果设f（t）为故障概率，或称为故障概率密度函数、失效密度函数，那么

R（t）、F（t）与f（t）的关系如图8-3所示。F（t）是图8-3中斜线部分的面积，R（t）是剩下部分的面积。由此还可得到：

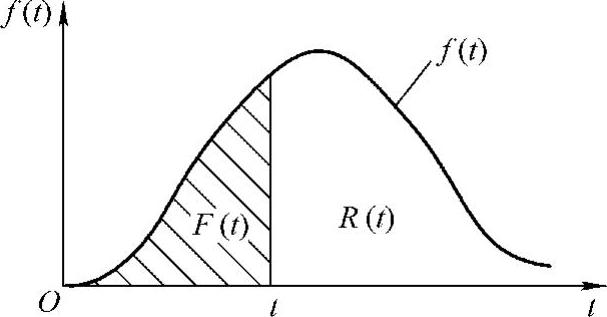
图8-3 故障概率函数(www.xing528.com)

瞬时故障率λ（t）是故障概率f（t）与可靠度R（t）的比值，亦即

由式（8-3）可知，

所以，故有

由式（8-6）可知，可靠度函数R（t）也可用瞬时故障率λ（t）来表示，或者说，可靠度是瞬时故障率的函数。

由图8-3和上述情况可知，产品失效数虽有其偶然性和随机性，然而在大量偶然现象中，却包含着必然性的规律，按数理统计的话说，失效的时间，是顺从一种分布的。只要分布函数f（t）或F（t）确定，则可靠度R（t）也就随之确定。不同的产品服从于不同的失效分布类型，也就是服从于不同的f（t）或F（t）的函数类型。

分布函数很多，例如威布尔分布，χ²分布、正态分布、t分布、二项分布、F分布、泊松分布、伽玛分布和指数分布等。