基于Liston模型的多轴汽车压实过程功的关系探究

在过去的三十年中，人们对雪地行驶阻力R_s的模型进行了许多研究，提出了各种模型。其中Liston（1974）提出的模型较为可行，因为该模型所需的雪地行驶系数可以通过测量得到。

Liston模型假定压实力与体积存在一定的关系，应用能量法对初始和最终体积的变化量进行积分，阻力R_s和水平距离的乘积等于压实过程中的功。其中，假定雪的横向滚动可以忽略，这样体积的变化可以用沉陷量来表达，具体表达式为

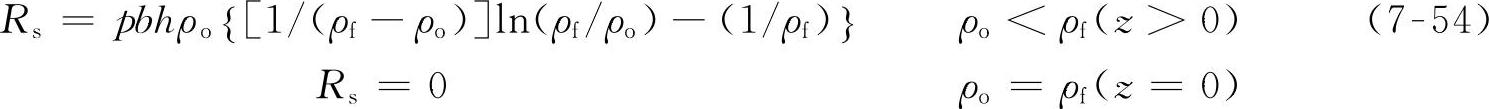
式中 p——轮胎气压（Pa）；

b——最大轮胎宽度（m）；

h——雪的厚度（m）；

ρ_o——初始雪密度（车轮轧过前）（kg/m³）；

ρ_f——最终雪密度（车轮轧过后）（kg/m³）；

z——沉陷量（m）。

在SSM1.0中，总牵引力与车轮对雪地的作用相关，其中车轮与雪的交接处雪的剪切力十分关键。剪切力与雪的内摩擦力和雪的粘性有关，根据Mohr-Coulomb原理，土壤的剪切失效关系为

式中 s——疲劳剪切强度（Pa）；

σ——正应力（Pa）；

c——内聚力（Pa）；

ϕ——内摩擦角。

乘以面积后得

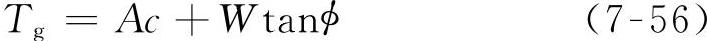
式中 A——轮胎的接地面积（m²）；

W——垂直力（N）。(www.xing528.com)

图7-17 雪的内聚力与 初始密度的关系

参数c和ϕ通过试验获得，图7-17为SSM1.0中使用的数据。该数据显示了不同初始密度ρ_o与c和ϕ的关系：

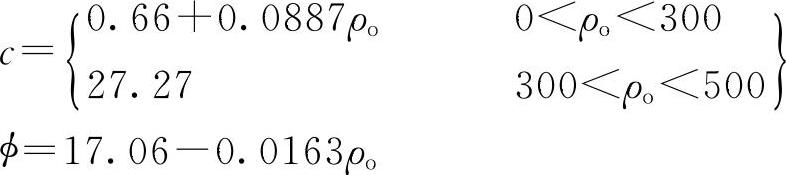
式中，c的单位为kPa，ρ_o的单位为kg/m³，ϕ的单位为（°）。

以上公式是指单一车轮的计算式，整车的牵引力计算要考虑所有车轮的计算结果后，进行求和计算，即总的静牵引力T_n为

轮胎的接地面积A由两部分组成（图7-18），其中A₁为曲面部分，该部分与雪的沉陷深度有关；A₂为压平的部分。

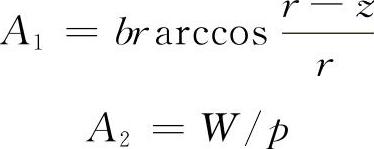
式中 r——轮胎半径（m）；

b——轮胎宽度（m）；

z——雪的沉陷量（m）。

轮胎的接地面积A为

A=A₁+A₂

美军通过大量试验研究表明：当雪的密度大于500kg/m³时，其行驶阻力系数很小，一般情况下为0.04～0.06，这与Yong提出的雪的临界密度是相符合的。Yong根据试验发现，当雪的密度大于500kg/m³时，在大多数的车辆作用下，雪地的压实沉陷量很小，因此车辆因压实地面所产生的行驶阻力系数很小。Yong将雪的密度500～550kg/m³称为雪的临界密度。当雪深小于10cm时，行驶阻力系数一般不大于0.08，当雪深的范围为10cm～20cm，行驶阻力系数一般为0.1～0.2。

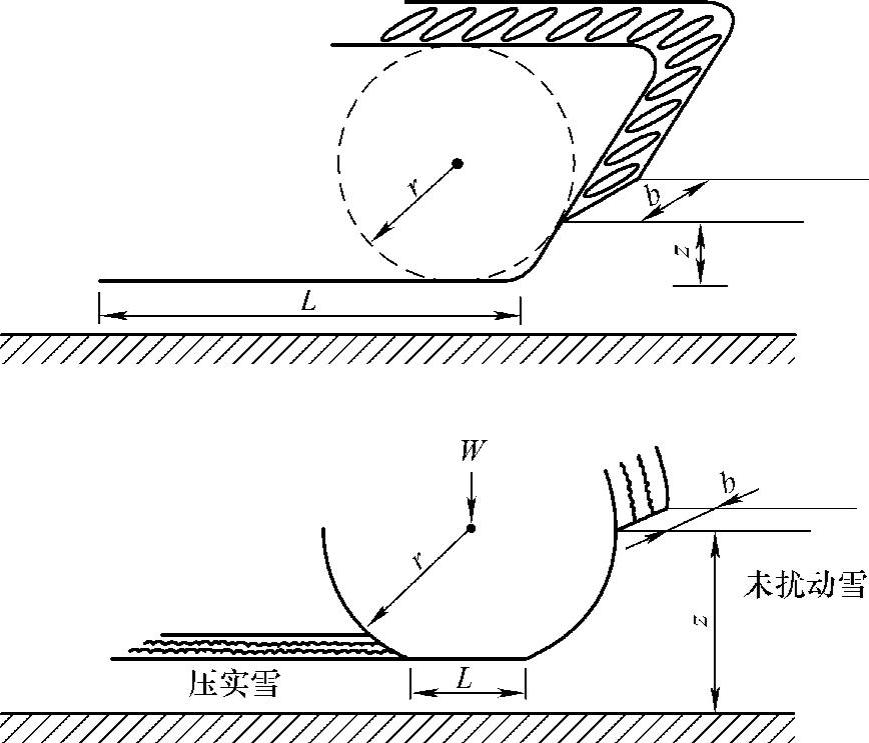
图7-18 轮胎与轨道的接触面积