多轴汽车超静定方法及越障高度分析

（一）数学模型

假设多轴汽车的轴数为n，第k轴越障，越障轴可以是驱动轴，也可以是从动轴。障碍系坚硬、垂直，高度为h的短凸台。若汽车在足够驱动力的作用下，车体绕簧外瞬心O转过了一个δ角，各车轴悬架弹簧产生了一个变形f_i和一个变形力P_i=f_iC_i。C_i为各轴弹簧的刚度。再假设整车载荷为P，簧外瞬心至整车质心面的距离（外心距）为R₀。质心面至第一轴的距离为l，各轴至第一轴的距离为l_i，那么便可通过图7-9的力学关系来建立多轴汽车越障高度的数学模型了。

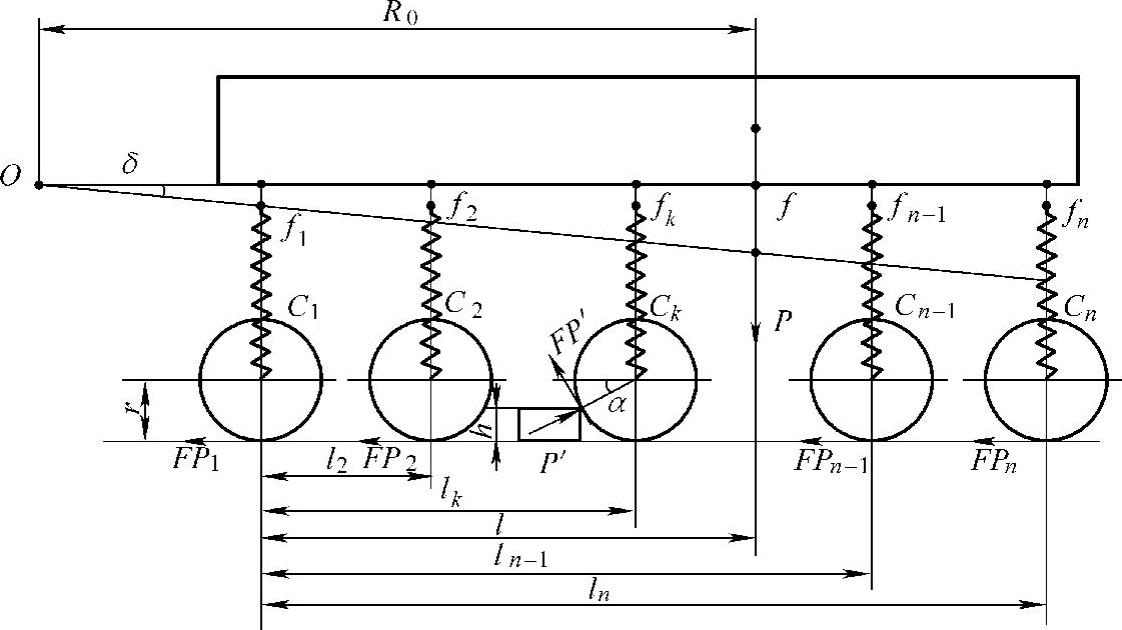
图7-9 多轴汽车跨越垂直障碍

根据水平方向力平衡的关系，即∑X=0的关系，可得如下方程：

式中 X_d——各驱动轴的驱动力；

X_r——各从动轴的滚动阻力；

X_o——作用于越障轴的阻力。

下面具体研究式（7-27）中的参数。

1.驱动力和滚动阻力

在假设P_i为各轴弹簧变形力，φ为附着系数，f为滚动阻力系数的情况下，各驱动轴的驱动力X_d=∑φP_i，而各从动轴的滚动阻力为X_r=∑fP_i。在第k轴为越障轴的情况下，驱动轴的驱动力和从动轴的滚动阻力可合并成为有效驱动力：

式中，F_i为各轴的接触系数，驱动轴为附着系数，即F_i=φ；从动轴为滚动阻力系数，取F_i=-f。

当越障车为全轮驱动汽车时，

式（7-28）中的P_i=f_iC_i，而各轴弹簧的变形f_i可由图7-9的几何关系求得，即

式中 f——整车质心处的变形。

于是各轴弹簧的变形力为

式（7-31）中的C_i是各轴弹簧刚度（单边悬架刚度的2倍）。

整车质心处的变形可表达为

式（7-32）中的P是整车负荷，C是整车质心面处的换算刚度，计算式为

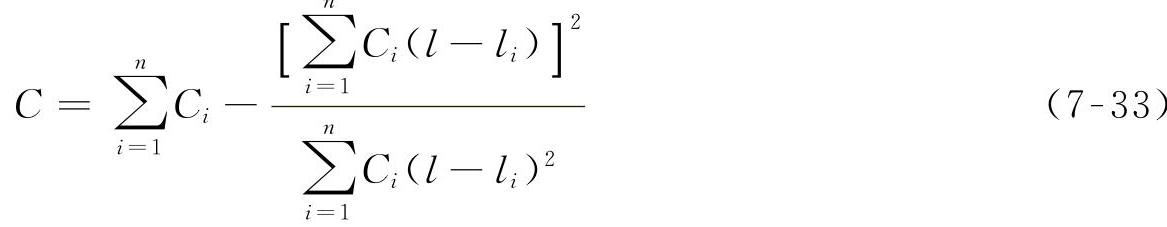
式（7-30）和式（7-31）中的R₀是外心距，它可用下式计算：

2.越障轮的阻力

作用于第k轴这个越障轮的水平载荷，也就是阻力x₀，可由图7-9的受力关系得到：

作用于越障轮向上的载荷，也就是托举力y₀，同样可由图7-9的受力关系得到：

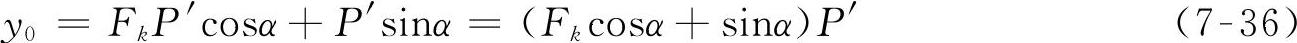
由于sinα=（r-h_k）/r，cosα=，式中，r为车轮半径，h_k为第k轴的越障高度。将sinα和cosα代入式（7-35）和式（7-36）后可得

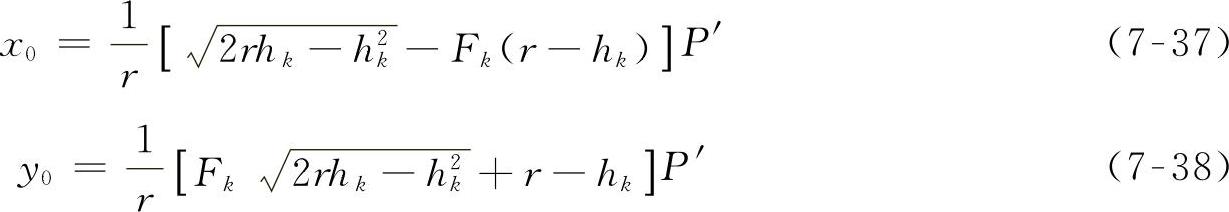
又因第k轴弹簧的变形为

故：

令式（7-38）等于式（7-39），便可得

将式（7-40）代入式（7-37），可得越障轮的阻力

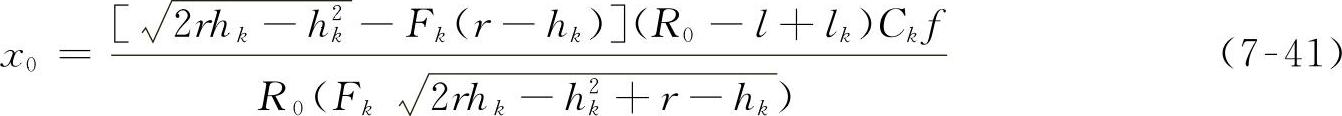
3.越障高度

将式（7-38）和式（7-41）代入式（7-37）可得S_k=x₀，亦即

解式（7-42），可得如下二次方程：

于是各轴越障高度为

若再设A_k=R_k+T_k，则

式中，，。

经进一步简化后，还可得到：

式中，，。

当为全轮驱动汽车时，

将式（7-46）代入式（7-45）后可得

（二）越障高度公式的分析

1.建式思路

越障高度式（7-45）的建立，是假定车轴越障时，车体绕外心转动，从而产生各轴的弹簧力和驱动力，进而按驱动力和阻力相等建立平衡方程。有关越障高度的因素，不仅考虑了整车负荷及其重心位置，而且也考虑了各轴的位置和刚度。特别还考虑了路面的附着状况和阻力状况等，因此式（7-45）必然具有较高的可行性。

2.适用范围

式（7-45）不仅适用于计算全轮驱动汽车各轴的越障高度，也适用于计算驱动轴和从动轴混列汽车车轴的越障高度；不仅适用于车轴数n>2的汽车，也适用于n=2的汽车。就拿负荷分配来说，用含有刚度C_i的式（7-31）计算的弹簧力与二轴汽车按杠杆比计算的负荷分配也完全一致。

3.h_k与r成正比

式（7-45）具有完美的数学形式，一看便知越障高度h_k是随车轮半径r的增大而增大的。正因如此，选装大尺寸的轮胎对提高通行能力是最为有效的。

4.h_k的取值范围

由式（7-45）可知，越障高度h_k的取值范围在（0～1）r之内。当M_k=0时，h_k=0；当M_k=N_k时，h_k=r。那么，M_k为零以及M_k=N_k的条件又是什么呢？

（1）h_k=0的条件 当越障车为全轮驱动汽车时，由式（7-47）可知，M_k=（φ_kP）²。因此，只要令式中的附着系数φ=0，M_k就将为零。此时，由于越障车失去了附着，失去了驱动力，故越障高度h_k也就为零了。

（2）h_k=r的条件 h_k=r，也就是h_k获得极大值，这要求解M_k=N_k时的φ_k值。当越障车为全轮驱动汽车时，根据式（7-47）和式（7-48），可以得到：

解此式可以得到h_k=r时的附着系数

h_k=r这个结果，从理论上说，一般是能够实现的。然而在下述情况又是不可能实现的。例如当式（7-49）中的时，P/P_k值就将小于2，即φ_kr值大于1。这是不可能的。这在三轴汽车中是普遍存在的，特别在后轴为双胎的二轴货车中更是有可能出现的！

5.h_k与φ的关系

上文已讲过，当φ=0，h=0；当φ=φ_r，h=r。在h获得极大值r之前，h总是随φ的增大而增大的。但曲线的具体形态则是与轴数n相关的。二轴汽车一般只有一个轴能在φ＜1时获得极大值。当φ＞φ_r后，h值就下降。当车轴数n≥3时，一般在φ＜1时，h都能获得极大值r。然而，过了极值点，h值依然下降，参见后文计算示例。注意，轴荷较小的车轴，出现极值点的φ值也较小。

6.h_k与轴荷P_k的关系

式（7-49）的φ_kr值是越障高度h_k获得极大值r时的附着系数。由该式可知，在同一辆汽车上，轴荷P_k较小的车轴，h_k获得极大值时的附着系数φ_k值较小。这就是说，轴荷较小的车轴能在附着条件较差的情况下，亦能越过较高的垂直障碍。

然而，在同一辆汽车上，某一车轴负荷较小，必然带来其他车轴负荷的增大，当障碍阻挡了高负荷车轴时，低负荷车轴以及整车也就不能通过了。因此，设计者的任务就是酌情使各轴负荷均布，也就是使各轴负荷趋于P/n值。

7.h_k与车轴数n的关系

在多轴汽车中，车轴数n越大，各轴负荷的均值∑P_i/n就较小，亦即P/P_k值就较大，由式（7-49）可知，h_k获得极大值时的附着系数，φ_k值就较小。例如二轴汽车（n=2），h_k获得极大值时的φ_k的均值趋近于1.0，而五轴汽车（n=5），h_k获得极大值时的φ_k的均值趋近于0.5。这就是说，汽车的轴数越多，在附着条件较差的环境下，亦能越过较高的垂直障碍。

8.混驱车与全驱车的比较

混合驱动汽车与全轮驱动越野车相比，其各轴的越障高度h_k在同等φ值下均大幅度下降。各轴的h_k达到极大值r的φ值也大大推后。特别是从动轴，虽有其他轴驱动力的推动，但由于自身失去了附着，h值就下降得更多，甚至在φ≤1的范围内不能达到极值点。

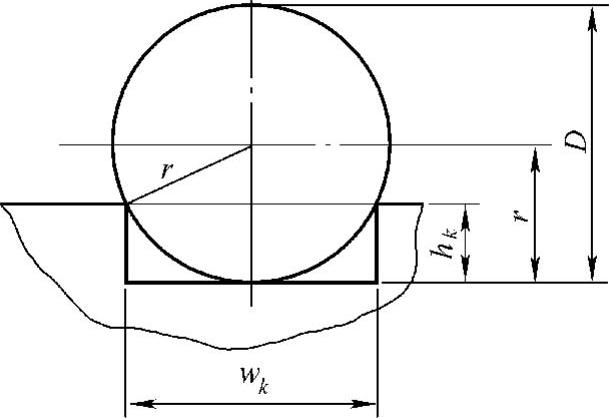
图7-10 越壕宽度

（三）跨越壕沟的问题

在已知越障高度h_k的情况下，可由图7-10的几何关系求得所能跨越壕沟的宽度w_k。(www.xing528.com)

（四）计算示例

1.某4×4越野车

有关参数：总负荷P=25988N，车轮半径r=385mm，整车质心至第一轴的距离l=1566mm；各轴至第一轴的距离l₁=0mm，l₂=2700mm；各轴悬架刚度C₁=54N/mm，C₂=85.4N/mm；取接触系数为F_k=φ=0.2，0.4…0.8，1.0。

具体计算：

1）利用式（7-34）计算外心距R₀，计算结果R₀=-19727.7mm。

2）利用式（7-33）计算质心换算刚度C，计算结果C=138.78N/mm。

3）利用式（7-32）计算质心处的变形f，计算结果f=187.26。

4）利用式（7-31）计算各轴弹簧力P_i，计算结果P₁=10914074N，P₂=15073N。

5）利用式（7-48）计算过渡参数N_k，计算结果列入表7-2之中。

表7-2 某4×4车型的N_k值与φ值的关系

6）利用式（7-47）计算过渡参数M_k，计算结果列入表7-3之中。

表7-3 某4×4越野车M_k值与φ值的关系

7）利用式（7-45）计算越障高度h_k，计算结果参见表7-4和图7-11。

表7-4 某4×4越野车h_k与φ的关系

图7-11 某4×4越野车h_k与φ的关系

8）用式（7-49）计算h_k的极大值点φ_kr，计算结果为φ_1r=0.851，φ_2r=1.175。

2.某6×6越野车

有关参数：总负荷P=73500N，车轮半径r=610mm，整车质心至第一轴的距离l=2000mm；各轴至第一轴的距离l₁=0mm，l₂=2400mm，l₃=4500mm；各轴悬架刚度C₁=265N/mm，C₂=275N/mm，C₃=255N/mm；取接触系数F_k=φ=0.2，0.4，0.6，0.8，1.0。

具体计算：

1）利用式（7-34）计算外心距R₀，计算结果R₀=-12403mm。

2）利用式（7-33）计算质心处的换算刚度C，计算结果C=778N/mm。

3）利于式（7-32）计算质心处的变形f，计算结果f=95.54mm。

4）利用式（7-31）计算各轴弹簧力P_i，计算结果P₁=29093N，P₂=25160N，P₃=19248N。

5）利用式（7-48）计算过渡参数N_k，计算结果列于表7-5之中。

表7-5 某6×6越野车N_k与φ的关系

6）利用式（7-47）计算过渡参数M_k，计算结果列于表7-6之中。

表7-6 某6×6越野车M_k与φ的关系

7）利用式（7-45）计算越障高度h_k，计算结果参见表7-7和图7-12。

表7-7 某6×6越野车不同φ值下的h_k值

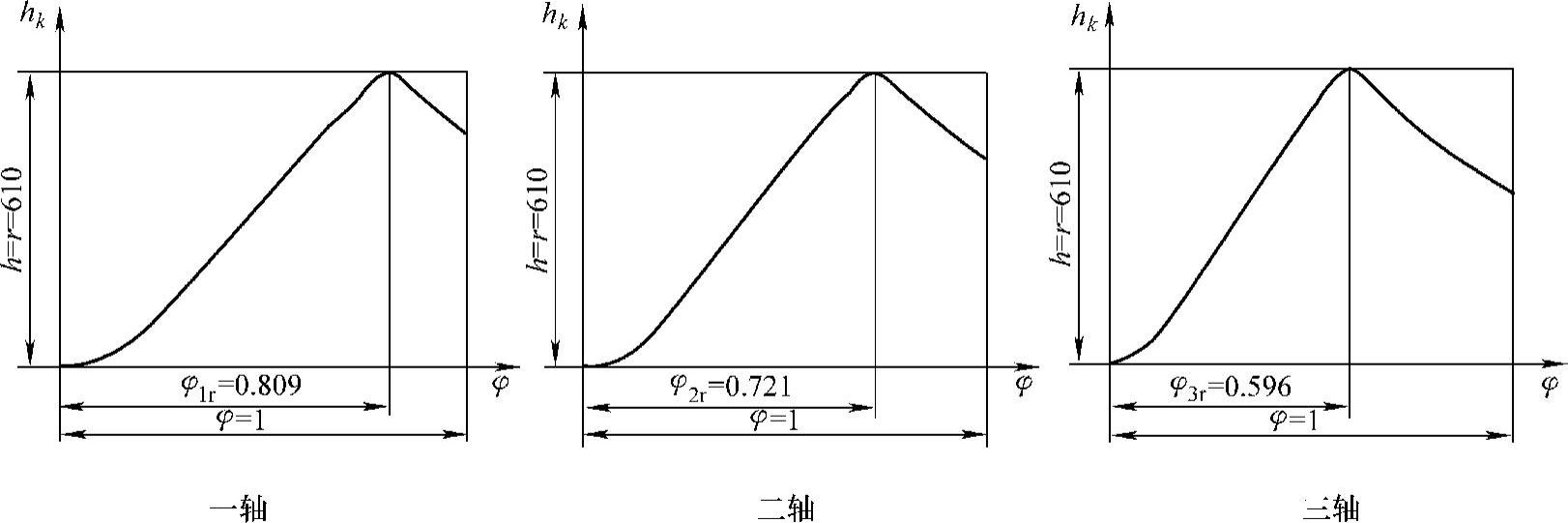
图7-12 某6×6越野车不同φ值下的h_k值

8）利用式（7-49）计算h_k获得极大值时的φ_kr值，计算结果为φ_1r=0.8094，φ_2r=0.7214，φ_3r=0.5956。

3.某8×8越野车

有关参数，总负荷P=286000N，车轮半径r=650mm，整车质心至第一轴的距离l=3700mm；各轴至第一轴的距离l₁=0mm，l₂=1950mm，l₃=5500mm，l₄=7000mm；各轴悬架刚度C₁=645N/mm，C₂=675N/mm，C₃=705N/mm，C₄=735N/mm；取接触系数F_k=φ=0.2，0.4…0.8，1.0。

示例计算：

1）用式（7-34）计算外心距R₀，计算结果R₀=-167144.7mm。

2）用式（7-33）计算质心处的换算刚度C，计算结果C=2759.24N/mm。

3）用式（7-32）计算质心处的变形f，计算结果f=103.65mm。

4）用式（7-31）计算各轴弹簧力P_i，计算结果P₁=68334N，P₂=70696N，P₃=72286N，P₄=74679N。

5）用式（7-47）计算过渡参数M_k，计算结果列于表7-8之中。

表7-8 某8×8越野车M_k与φ的关系

6）用式（7-48）计算过渡参数N_k，计算结果列于表7-9之中。

表7-9 某8×8越野车N_k值与φ值的关系

7）用式（7-45）计算越障高度h_k，计算结果参见表7-10和图7-13。

表7-10 某8×8越野车不同φ值下的h_k值和w_k值

8）用式（7-49）计算h=r点的φ_kr值，计算结果参见表7-10和图7-13。

9）用式（7-50）计算越壕宽度w_k，计算结果列入表7-10之中。

图7-13 某8×8越野车不同φ值下的h_k值

4.某8×6汽车（第四轴为从动轴）

本车型系上述8×8车型的变型，故基本参数相同。附着系数仍取为0.2，0.4，…0.8，1.0；滚动阻力系数取为f=0.02。已计算参数有：R₀=-167144.7mm，C=2759.24N/mm，f=103.65mm；P₁=68334.2N，P₂=70696.3N，P₃=72286.3N，P₄=74678.6N。

补充计算：

1）用式（7-28）计算有效驱动力S_k，计算结果列入表7-11之中。

表7-11 某8×6汽车S_k值与φ值的关系

2）用式（7-47）计算过渡参数M_k，计算结果列入表7-12之中。

表7-12 某8×6汽车的M_k值与φ值的关系

3）用式（7-48）计算过渡参数N_k，计算结果列入表7-13之中。

表7-13 某8×6汽车的N_k值与φ值的关系

4）用式（7-45）计算越障高度h_k，h_k=（1-）r，计算结果参见表7-14和图7-14。

表7-14 某8×6汽车h_k与φ的关系

图7-14 某8×6汽车不同φ值下的h_k值

（五）结论

1）采用超静定方法建立的多轴汽车越障高度h的计算公式，它不仅是一显式函数，且既适合驱动车轴，也适合从动车轴。

2）多轴汽车的越障高度h是和车轮半径成正比的，因此选装大尺寸的轮胎对越障行驶是有利的。

3）多轴汽车的越障高度h，开始是随附着系数φ的增高而增高的，当h达到极大值r后又反随φ值的增高而减小。然而，选用宽断面变气压和优质胎面的轮胎亦是可取的。

4）轴数n越大，h出现极大值r时的φ值越低，反之越高；二轴汽车负荷较高的车轴以及三轴以上汽车的非驱动轴其越障高度一般不可能达到车轮半径。

5）多轴汽车轴荷较小的车轴，或者说车轴数n大的汽车均有利于越障行驶。

6）由于多轴汽车轴荷较小的车轴，在φ值较小时，就能越过较高的垂直障碍，因此，使各轴轴荷P_i均布或趋于P/n值，则有利于整车超越障碍。

7）越壕宽度w是随越障高度h增大而增大的，当h=r时，w=2r。

总之，选大胎，增附着，加轴数，均载荷是提高越障高度的有效措施！