转矩和为零的方法及多轴汽车的应用

1.数学模型

假设多轴汽车的轴数为n，车轮半径为r，各轴弹簧的刚度为c_i，整车负荷为P，各轴的法向反力为w_i；l为整车重心至第一轴的距离，l_i和l_j为各轴至第一轴的距离，第k轴为越障轴，l_k为越障轴至第一轴的距离；F_i为各轴的接触系数，驱动轴为附着系数，即F_i=φ；从动轴为滚动阻力系数，取F_i=-f。

第k轴越障时的力学关系如图7-8所示。

根据图7-8的力学关系，可以得到下列平衡方程：

1）当k轴越障时，各轴反力对P_j点取矩所得的（n-1）个方程：

式中，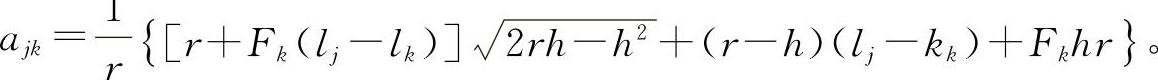

2）当k轴越障时，各轴反力对P_k点（i=k）取矩所得的一个方程：

图7-8 多轴汽车超越垂直障碍

式中，a_ki=F_kh+l_k-l_i-。当i=k时，a_kk=0。

3）当k轴越障时，由全部垂向力之和为零（∑Y=0）可得：

(https://www.xing528.com)

在式（7-22）、式（7-23）和式（7-24）中，共有[（n-1）+1+1]=n+1个方程，而未知数也恰好是n+1个，因此可求解全部未知数。

由式（7-24）可以解得

式中

2.计算方法

有了上述的数学模型，便可按下列步骤计算第k轴的越障高度了。

1）由式（7-22）和式（7-23）可以得到一个n阶矩阵：

AW=B （7-26）

2）把越障高度视为一个已知数H₀（初试高度，可取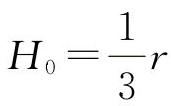，输入矩阵方程，这样便可解得各轴垂直反力w_i。

3）把所得w_i代入式（7-25），又能得到一个H（k）值。

4）令ΔH=|H₀-H（k）|，若此值大于一个规定的步长数ST，则重新输入新的H值（H=H₀+S×ST），这样便可得到一组新的垂直反力w_i和H（k），如此循环往复（迭代法），直至ΔH<ST为止，此时的H（k）值便是所求的第k轴的越障高度。

下面写出n阶矩阵的具体表达形式：