多轴汽车：车身下危险点纵向通过角分析

1.定义

GB/T 3730.3—1988对纵向通过角的定义如下：“当分别切于静载车轮前后轮胎外缘且垂直于y平面的两平面交于车体下部较低部位时，车轮外缘两切面之间所夹的最小锐角。该角为车辆可以超越的最大角度。”

这个定义更是值得研究：

问题之一是，只考虑了切于轮胎外缘的情况，没有考虑不可能相切的情况。事实上，作为纵向通过角，绝大多数是不可能相切的。

问题之二是，车体下部较低部位中的“较低部位”一词未能说明问题的本质。因不光是高或低的问题，而关键是危险的程度，是相碰的可能性。Z坐标较高的点有可能比Z坐标较低的点还危险。

车身下部哪一个点的纵向通过角最小呢？这需要具体分析。一般来说，车体下部某点的X坐标越是靠近两轮距离L的处，且Z坐标又越小时，则过该点所做的纵向通过角就越小，该点就是所谓的危险点，如图7-4所示。

图7-4 纵向通过角的比较

由此可知，纵向通过角应按下文定义：

纵向通过角系在满载静状态下，过车身下部危险点（最易碰触点）的两个平面之间所夹的锐角。这两个平面既须垂直于yz平面，还须或分别切于前部或后部轮胎外缘（地上部分），或分别过前部（或后部）轮胎与地面的交点（或交线）。(www.xing528.com)

2.数学表达式

在图7-4中，D点在x方向靠近处，但Z坐标（从地面计起）较高；而P点在x方向远离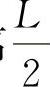处，但Z坐标却较低。到底哪一点的纵向通过角最小呢？是α_D还是α_P呢？这需要

具体的检验计算。计算可以判定真正的危险点，还可考察其是否满足战术技术要求。纵向通过角可用式（7-5）计算：

式中 α——纵向通过角（°）；

α_f、α_r——前、后部轮胎的通过角（°）。

α_f和α_r可采用式（7-1）或式（7-2）计算，到底采用哪一式计算，仍可利用式（7-4）

判定。值得注意的是，在计算α_r时，坐标应取为（L-X）。