汽车通过角：接近角和离去角的计算公式

接近角和离去角均是汽车的通过角，皆为关系汽车通行能力的表征参数。由于这些参数貌似简单，故未得到人们的足够重视。不仅没有从数学高度去表述它们，而且有关其定义都不甚严谨。

1.定义

关于接近角和离去角概念的定义，存在很多分歧，本书认为：

假设当车身前下部的危险点（最易碰触的点）D的x坐标很大，而z坐标又很小时，那么过D点且与轮胎外缘相切的平面，所切部位只能在地面之下，如图7-1所示。

所切部位只能在地面之下是不能接受的。若设危险点D的z坐标（从地面计起）为零，则此时的接近角便是负值。事实上，此时的接近角应该是零度。由上述情况可知，接近角应按下文定义：

接近角系在满载静状态下，xy平面与P平面所夹之锐角。而P平面或为过车身前下部危险点（最易碰触点）D，且与轮胎外缘（地面部分）相切而同时又垂直于yz平面的平面；或为过危险点D和轮胎外缘与地平面的交线A-A而同时又垂直于yz平面的平面。

离去角与接近角类同，不再赘述。

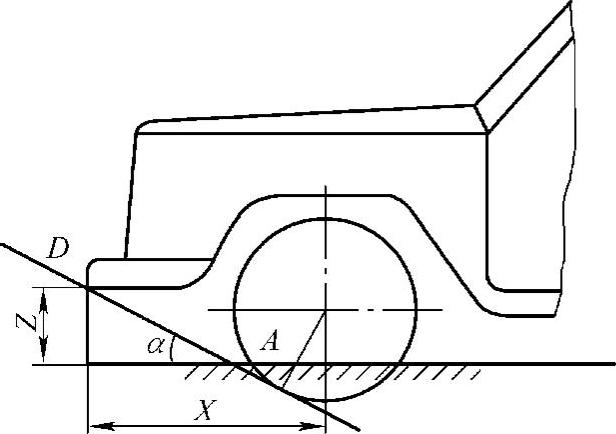
图7-1 接近角的定义

2.数学表达式

为满足战术技术要求，在对车辆前下部的某些总成部件，例如转向机、绞盘等进行布置安装时，对接近角进行检验计算是很有必要的。

计算公式可按两种情况建立：

当P平面可与轮胎外缘地上部分相切时，可根据危险点D的坐标值X、Z，利用图7-2的几何关系，导出接近角（离去角类同）的数学表达式：

图7-2 接近角（可切）

式中 α——接近角（离去角）（°）(www.xing528.com)

X——危险点D的x坐标；

Z——危险点D的z坐标；

R——轮胎的自由半径；

R_k——轮胎的静力半径。

当P平面不可能与轮胎外缘地上部分相切时，仍可利用危险点的坐标值，根据图7-3的几何关系，导出接近角（离去角）的数学表达式：

作为具体的车辆，上述两种情况到底属于哪一种呢？到底采用式（7-1）还是采用式（7-2）计算呢？

当总布置图已经绘出，从图上可以一目了然。然而，当根本没有绘制图样，只是对某一总成试行布置，估计到该总成的某一部位可能就是危险点时，则应根据危险点的坐标值加以判定。

对此，需要建立一个坐标判别式。首先需要确定P平面从可切到不可切的临界接近角（离去角）。由于临界状态处于P平面与车轮半径相垂直的位置，故临界接近角（离去角）α_c可由式（7-3）表示：

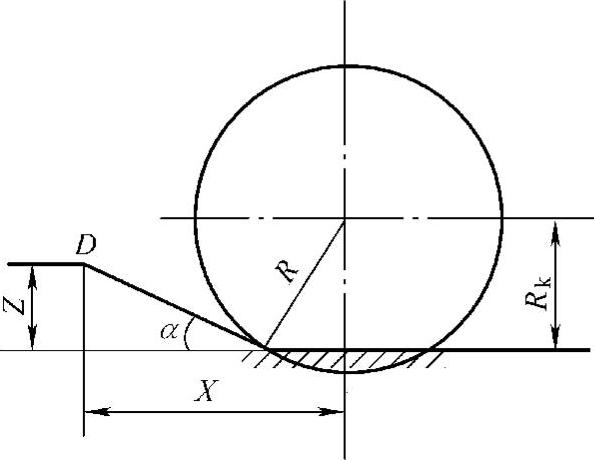
图7-3 接近角（不可切）

当令式（7-2）等于式（7-3）时，便可解得临界位置危险点D的坐标X与Z的关系式：

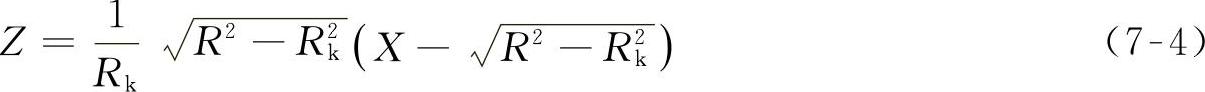
由式（7-4）可知，当需要考察的点的坐标X确定之后，那么危险点的Z坐标就可由式（7-4）求出。如果被考察点的Z坐标值小于计算值，那么接近角（离去角）则应采用式（7-2）计算，反之采用式（7-1）计算。