如何选择多轴汽车球头中心位置

汽车转向系在总布置中需要确定节臂球头中心和垂臂球头中心的空间位置，以及直拉杆的形状等。

两球头中心的空间位置是关键：它关系到车桥和转向系统运动的干涉问题；关系到转向的轻重、向左转和向右转的转向力矩是否接近以及直拉杆的空间位移量是否过大等问题，还关系到直拉杆的直线长度。车轮的转动、弹簧、减振器、稳定杆等的位置一起决定着直拉杆的形状。此处仅研究车桥和转向系统运动的干涉问题。

（一）轨迹矛盾问题

行车中，由于车桥的跳动，刚化固定在车桥（非悬挂质体）上的元件的任何点都将绕各自的中心，以一定的轨迹半径作近似的圆弧运动。节臂球头中心正是这样的点（相关点）。直拉杆式的转向系统，桥上的节臂球头中心连接着直拉杆的一端，车身（悬挂质体）上的垂臂球头中心连接着直拉杆的另一端。车桥跳动时，假设垂臂球头中心不动，那么，节臂球头中心又将以垂臂球头中心为圆心、以直拉杆的直线长度为半径作圆弧运动。同一个点，同时作两个圆弧运动，两个圆心不一定重合，两个半径不一定相等，因此运动是矛盾的，如图6-37所示。

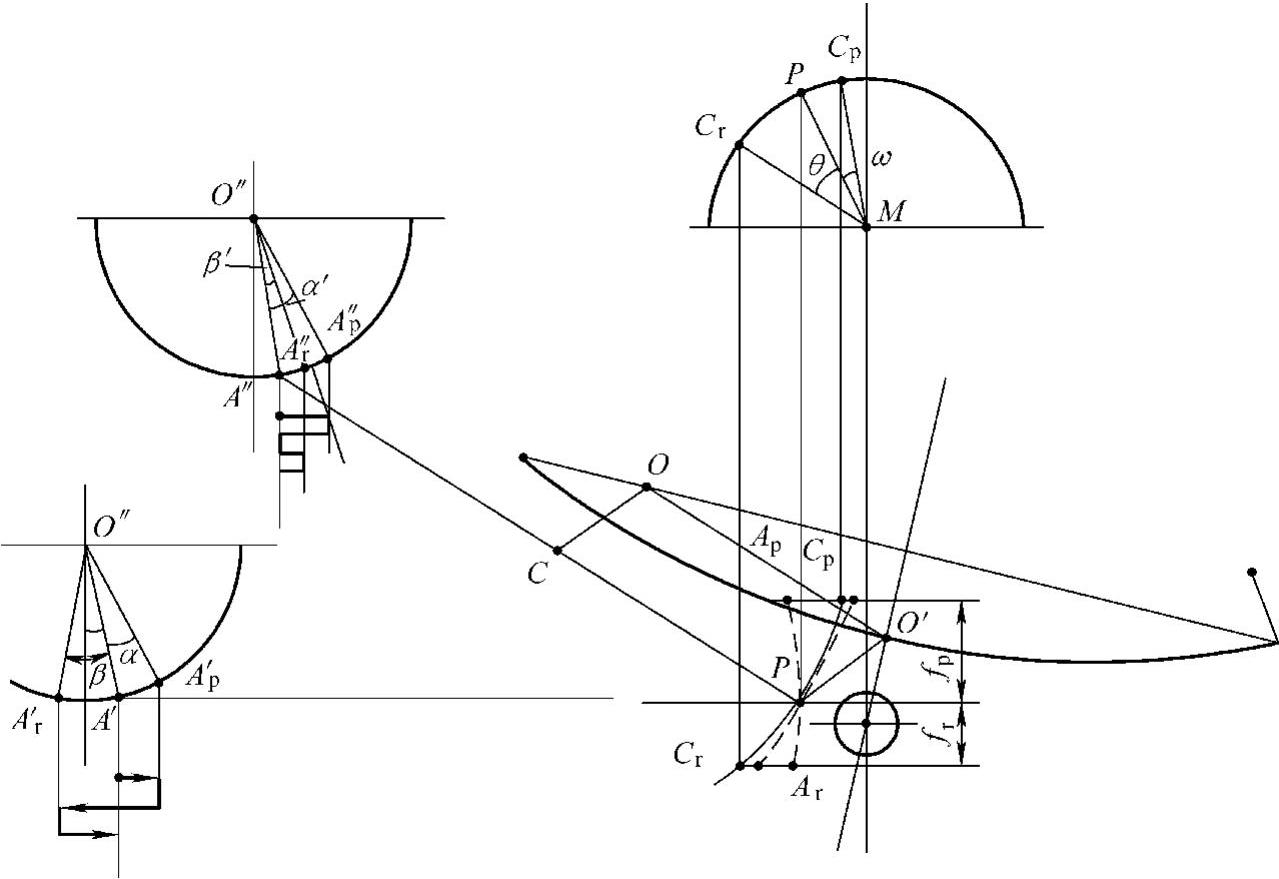
图6-37 球头中心位置与运动干涉的关系

图中，A是垂臂球头中心，P是节臂球头中心，O是钢板弹簧主叶片中心O'的轨迹中心，C是相关点P的轨迹中心。在对称簧中

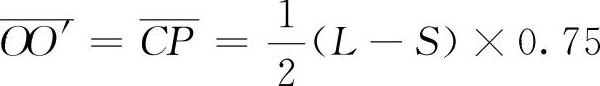
式中，L为弹簧主片伸直长度；S为夹紧长度。弧线C_rC_p是以C为圆心、CP为半径画出；弧线A_rA_p是以A为圆心、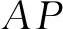为半径画出。

动挠度为

式中，f_静为满载静挠度；λ值参照“汽车设计”取值。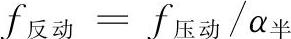

式中，α_半为半周期衰减系数，α_半=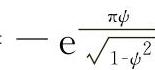，ψ是悬架系统相对阻尼系数（阻尼化）。ψ=0.25，则α_半=-22.5；ψ=0.3，则α_半=-2.68。负号说明f_反动在满载静状态平衡位置P点之下。由f_压动所决定的水平线和C_rC_p弧交于C_p点，和A_rA_p弧交于A_p点。直线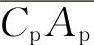代表压缩终极位置的矛盾量，直线代表着反弹终极位置的矛盾量。

假若垂臂球头中心A点可绕O″点转动，（P点不动），并设A、P两点在同一垂直平面上，那么A'_p点就是以O″点为圆心、以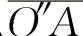为半径所画的圆弧与以C_p点为圆心、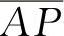为半径所画弧的交点。按相似步骤，可画出A'_r点。也就是压缩时，垂臂向右转过α角，反弹时，垂臂向左转β角。α和β也代表着机构的矛盾量。若方向机构是可逆的，那么，转角α和β最终反映到转向盘上。转向盘转角向右为α_d=i_α，向左为β_d=i_β。由于转向器的速度比i值一般不小于15，所以α_d、β_d是可能达到很大数值的。假若节臂球头中心P点可绕主销中心M点转动（A点不动），由于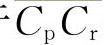弧是P点必经的轨迹，所以节臂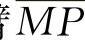压缩时转过了ω角，反弹时反转了θ角。ω和θ也代表着机构的矛盾量。它最终反映到车轮的偏转上。节臂的转角也就是车轮的转角。

总之，这一机械的矛盾，必将由下列三种情况之一来解决：

1）假若转向盘抓得很紧（A点不动），地面阻力又很大（P点不动），那么车桥跳动时，只能以克服各部关节点的间隙，或者机件产生弹性变形和损坏来统一矛盾。

2）假若转向盘抓得不紧（A点可动），地面阻力却很大（P点不动），那将造成转向盘来回打摆。这种情况下，在高速通过凹凸不平较大的地面时，转向盘就有脱手的可能。车辆原地不动，丢开转向盘，若干人在车上一齐闪动，就类似这种情况。(www.xing528.com)

3）假若转向盘抓得很紧（A点不动），地面阻力却很小（P点可动），行车时，将出现车轮摆转，车辆摆头绕行。高速行经光滑路面时，这种可能性较大。值得注意的是：随着球头中心A、P两点位置的不同，运动的矛盾量（也就是垂臂的摆角）也将不同。在图6-37中，若球头中心A点移至A'点，垂臂摆角就是α'和β'，显然图6-37中的α'＜α，β'＜β。也就是说，A'点优于A点，因而矛盾量较小。

（二）摆振的频率问题

车桥和方向机构运动的轨迹矛盾，带来转向盘或者车轮的偏摆振动。上节所谈的矛盾量，就是偏摆振动的振幅。除此之外，还存在一个振动频率的问题。在图6-37中，A点的振动，是从A到A'_p，再从A'_p过A到A'_r回到A，即车桥跳动一次，垂臂和转向盘也摆动一次。若设车桥振动频率为n，转向盘摆振频率为N，则在A点是N=n的全波振动。

然而，随着垂臂球头中心位置的变化，摆振频率也发生变化。在图6-37中，A'点在车桥跳动一次时，它的振动过程是：A'→A″_p→A'→A'_r→A'，显然，这是N=2n的半波振动。频率高了，带来的问题是转向盘（或车轮）振动加速度大，此外，关节部位磨损加快。

（三）矛盾的协调统一

由前述可知：车桥和转向系统的运动干涉问题，是和球头中心A、P两点的位置紧密相关的。那么，什么位置为较好呢？从原则上说，那就是两条：第一，摆幅越小越好；第二，摆振频率越小越好。矛盾量α=0、β=0，摆振频率N=n，是最理想的位置。也就是垂臂球头中心A和节臂球头中心P的轨迹中心C相重合为最理想。但从结构上看，这一般是难以做到的。但近似的做法是调整A、P两点的位置，争取：①A、C两点在桥心的同一侧；②A在接近于C—P连线且稍偏离下方处；③A、C距离尽可能减小。在这几点中，单就某一点来说并不一定有利。如A、C虽在同侧，但若A点的具体位置选得不好，还可能不如A、C异侧好。

下面我们根据减小矛盾量和频率的原则，进行具体分析选择。先假定节臂球头中心P和直拉杆长度AP已定，A、C同侧，对称钢板弹簧，并设A、P两点在同一垂直平面上。如图6-38所示，弧线PP是以P圆心、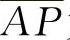为半径画出的，也就是说垂臂球头中心就是在这条弧线上选择。当f_p和f_r给出后，就决定了C_p和C_r两点，再分别以C_p、C_r为圆心、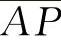为半径，就画出了和。这两条弧线就表示出压缩和反弹时垂臂的偏转量。这

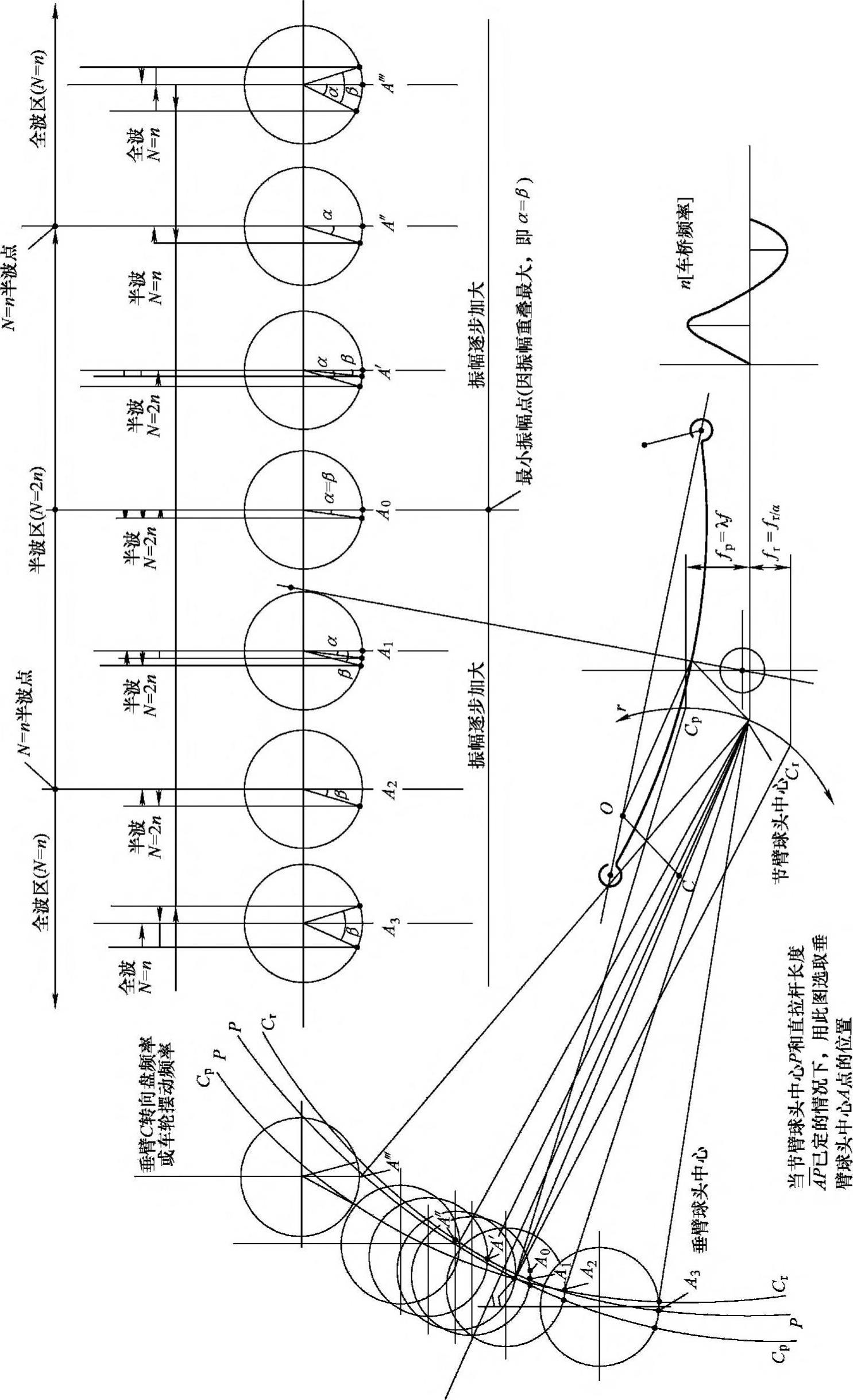
图6-38 车桥和转向系统运动干涉的分析选择

两条弧线分别和相交于A₂点和A″点。从振动频率看，这两点是N=2n的半波点，区间[A₂，A″]是N=2n的半波区，区间外皆为N=n的全波区。C_pC_p弧和C_rC_r弧有一个交点F，若垂臂球头中心A₀点的轨迹经过F点，那么A₀点就是最小振幅点。因压缩和反弹的矛盾量相重叠，即α=β，A在PP弧上离A₀点越远，则振幅越大。

综合矛盾量和振动频率来看，还是选A₀点为合适。虽然频率较[A₂，A″]区间以外高一倍，但振幅最小。微小振动，转向盘是不致脱手的。如果位置不允许，要在靠近A₂点或A″点处选取，那么不如就选A₂点或者A″点好。因为和全波区比，频率相等，振幅却小；和半波区比，虽振幅最大，但和邻近点相差甚微，相反，频率却减小一倍按同样的道理，我们也可变化的长度（直拉杆的长度）选择。若在A点位置没有选择余地的情况下，也可变化P点的选择。如一些车型，节臂做成既弯又斜的形状，就是在调整P点的位置。

原则就是减小振幅和频率，以减少振幅为主。

从上述分析中，已知A₀点是较理想的。但在已知和F点，以及垂臂长度的情况下，怎么确定A₀点呢？这可利用图6-39来确定。过F点作一铅垂线，并以F点为圆心、垂臂长为半径画圆，此圆和铅垂线交于S点。再以S点为圆心、垂臂长为半径画弧，此弧与交于一点，此点即是A₀点。

如果垂臂有一初相角λ，则可过F点作一铅垂线；并以F点作顶点，作一与此铅垂线成λ角的线，此线与以F点为圆心、垂臂长为半径所画的圆交于S点；再以S点为圆心、垂臂长为半径画弧，此弧与交于一点，则此点就是A₀点。

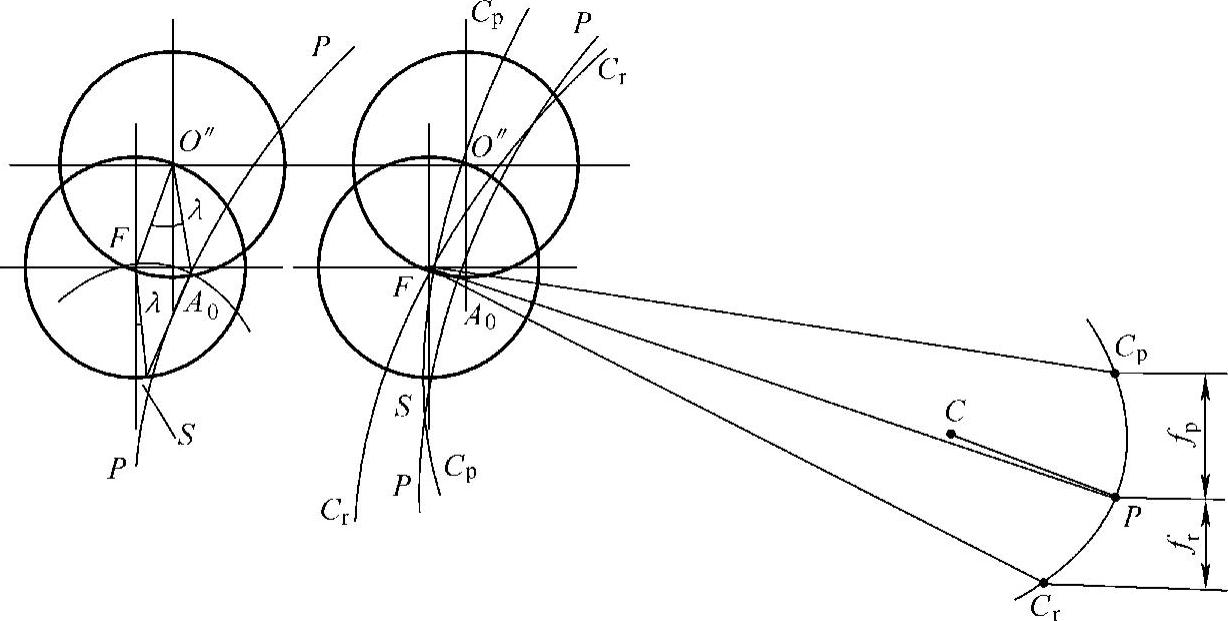
图6-39 A₀点的确定