多轴汽车：转向系传动比变化特性分析

（一）传动比的组成及定义

转向器的传动比由角的传动比iωo和力的传动比i_p组成。

1.角传动比i_ωo

角传动比i_ωo是转向盘的转角φ与驾驶人同侧转向轮转角之比。它包括转向角传动比i_ω和转向传动装置的角传动比i'_ω。

转向盘的转角φ和转向摇臂轴的转角β_p之比，称为转向器的角传动比，即i_ω=φ/β_p。转向摇臂轴的转角β_p与转向节臂转角β_k之比，称为转向传动装置的角传动比i'_ω，即i'_ω=β_p/β_k。

2.力传动比i_p

力传动比i_p是从轮胎接地中心作用在两侧转向轮上的合力2F_ω与作用在转向盘上的手力F_h之比，即i_p=。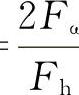

（二）力传动比与角传动比的关系

如上所述，力传动比可用式（6-87）表示：

轮胎和地面之间的转向阻力F_ω和作用在转向节上的转向阻力矩M_r，有以下关系：

式中 a——车轮转臂，指主销延长线至地面的交点到轮胎接地中心的距离。

作用在转向盘上的手力F_h可由式（6-89）表示：

式中 M_h——作用在转向盘上的力矩；

R_sω——转向盘作用半径。

将式（6-88）和式（6-89）代入式（6-87）后得

如果忽略摩擦损失，2M_r/M_h可用式（6-91）表示：

将式（6-91）代入式（6-90）之后得(www.xing528.com)

由式（6-92）可知，力传动比与R_sω、a和i_ωo有关。车轮转臂a越小，力传动比i_p越大，转向越轻便。但a值过小，会由于车轮和路面之间表面摩擦力的增加，反而增大了转向阻力。对于一定车型，可用试验方法确定a值的最小极限。通常货车的a值在40～60mm内，轿车的a值取0.4～0.6轮胎胎面的宽度。转向盘半径R_sω根据车型大小在200～275mm范围内选取。对于一定的汽车而言，R_sω和a都是一个常值，故力传动比i_p与角传动比i_ωo成正比关系。

（三）转向系的角传动比i_ωo

转向传动装置的角传动比i'_ω可用转向摇臂轴转角β_p与转向节臂转角β_k之比来表示，也可以近似用转向节臂臂长l₂与摇臂臂长l₁之比来表示，即

现代汽车结构中l₂和l₁的比值，一般为0.85～1.1，可粗略地认为其比值为1，所以转向传动装置的角传动比i'_ω近似为1，则

即转向系的角传动比，近似等于转向盘的转角和转向摇臂轴转角之比。于是，研究力传动比i_p和转向系角传动比i_ωo及其变化规律的问题，可以归结为只研究转向器角传动比及其变化规律的问题。

（四）转向器角传动比及其变化规律

转向器角传动比i_ω是一个重要参数，它影响汽车的操纵轻便性、转向灵敏性和稳定性。由式（6-92）能看出：增大角传动比可以增大力传动比。而式（6-87）表明，在转向阻力F_ω一定时，增大力传动比i_p会减少驾驶人作用在转向盘上的手力F_h，使操纵轻便。

由式（6-91）并考虑到i_ωo≈i_ω，则能看出：转向轮的转角和转向器角传动比i_ω成反比。角传动比增加后，转向轮转角对同一转向盘转角的响应变得迟钝，操纵时间增长，汽车转向灵敏性降低，所以“轻”和“灵”构成了一对矛盾。为解决这对矛盾，通常采用可变角传动比的转向器来协调这对矛盾。变传动比的变化规律，又因转向器的结构形式和参数的不同而有所差异。

图6-31所示为蜗杆曲柄销式转向器的工作简图。销子与蜗杆接触点A、传动中心O的距离是不固定的。转向盘转动一周，销子由图上的A点位置将移动一个螺距t，若转向盘转动一个φ角，销子的距离是s，则有

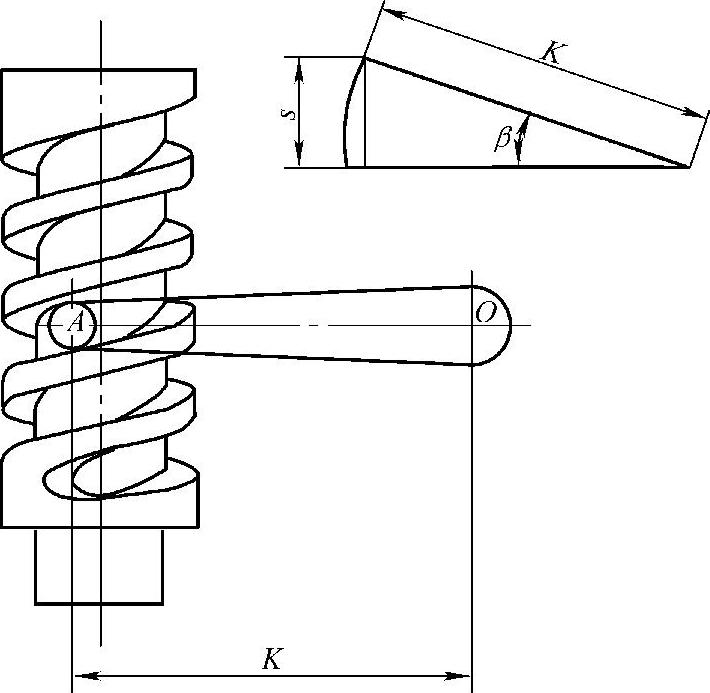
图6-31 蜗杆曲柄销式转向器

由图6-31可知

所以

如果曲柄长为K，螺距t不随φ角而变，则

式（6-98）表明当螺距t不变时，角传动比i_ω和转角β_p的余弦成正比。故在直线行驶位置附近，转向器角传动比i_ω比在其他位置要大，所以在小转弯行驶时获得了较好的操纵轻便性。当指销离开中间位置走向两端时，角传动比的值逐渐下降，根据公式β_h=φ/i_ω可知，此时转向轮对转向盘转角的响应变得比较敏感。转向盘旋转总圈数得以减少，这样在一定程度上解决了“轻”和“灵”的矛盾。根据使用要求，有的汽车希望角传动比在直线行驶位置附近有较小值，在两端有较大值，对此，蜗杆曲柄销式转向器可通过改变螺距t来达到这一要求。

对单销式转向器而言，设计者可根据要求把每处螺距设计成所需要的值，以获得所要求的角传动比变化规律。例如某车型转向器蜗杆，中间位置附近螺距t较小，到两端逐渐增大，其传动比在中间位置等于19，转向盘从中间位置向两边转30°仍然不变。转向盘从30°转动到75°，传动比从19急剧减低到11，之后从75°开始缓慢减小，当摇臂轴转到底时减至8。蜗杆中间位置附近螺距t较大，到两端逐渐变小。