普通梯形机构及转向特性分析

普通梯形机构也叫整体式梯形机构，由两个梯形臂和一根横拉杆组成。梯形机构有前梯形和后梯形之分，如图6-15所示。图中M为主销中心距，m为梯形臂，θ为梯形角。

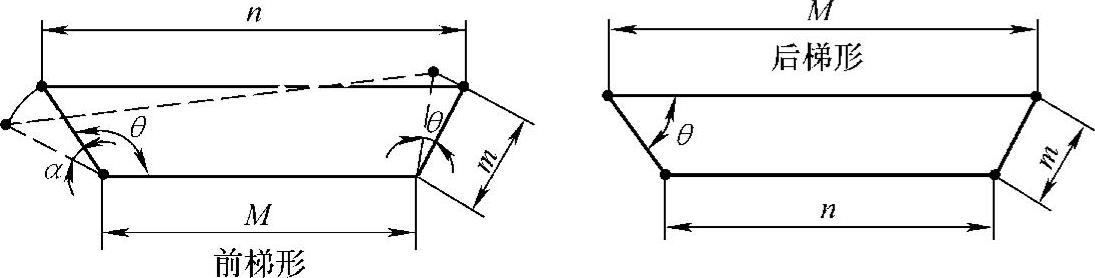
图6-15 整体式梯形机构

（一）内外轮转角关系

当给定一个内轮转角α值后，由梯形机构的运动学关系可以得到相应的外轮转角β值，即

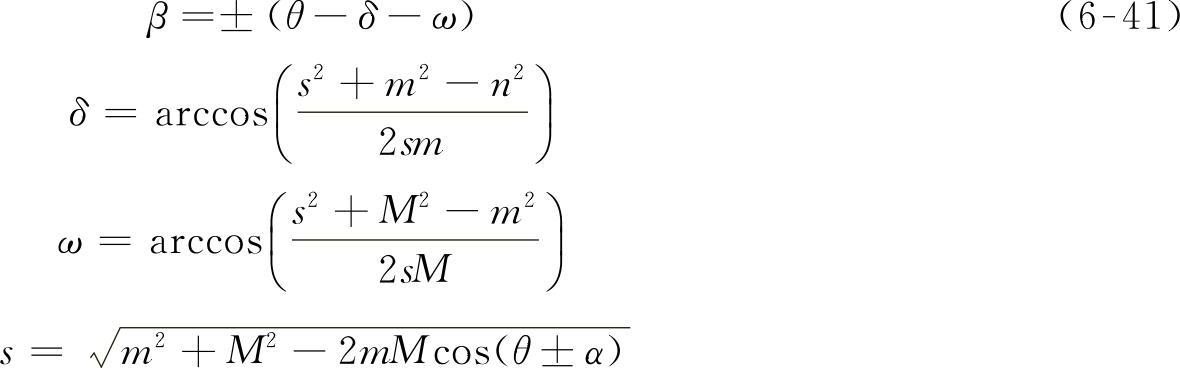
式中 α——内轮转角（°）；

β——外轮转角（°）

θ——梯形角，即梯形臂m与M线的夹角（°）；

M——主销中心距；

m——梯形臂的长度；

n——两梯形臂球头中心距。

另外，式中的“±”号，前梯形取正，后梯形取负。

有了梯形机构的内外轮转角关系式，就可以解决如下两个问题：

1）计算对应于内轮转角的汽车转弯半径。

2）判定梯形机构的转向特性。

（二）梯形机构的转向特性

刚性车轮无滑移转向的条件是

式中 L_t——无滑移轴距（mm）；

M——主销中心距（mm）；

α、β——内外轮转角（°）。

式（6-42）中所给的条件，便是所谓的中性转向趋势。在轴距和梯形机构已定的情况下，要想始终保持这种转向，既无必要也无可能。不过有一个通常的参考，那就是cotθ=0.75M/L，m=0.11～0.15M。

对于一定的梯形机构，当给定了一个内轮转角α之后，相应的外轮转角β就被完全确定了。

内外轮转角一定，即完全确定了车辆的运动瞬心和转弯半径。若将此时的内外轮转角带入式（6-42），由此算得的无滑移转向的理论轴距L_t，与实际的轴距L_p就不见得一致了。L_p可能大于L_t，也有可能小于L_t。它们的关系见式（6-43）：

式中 λ——轴距系数；

L_p——实际轴距（mm）；

L_t——无滑移转向轴距（mm）。

轴距系数不仅反映了实际轴距与梯形机构所决定的无滑移转向轴距之间的关系，而且反映了不同的转向特性趋势：

•λ＞1，为不足转向趋势；

•λ=1，为中性转向趋势；

•λ＜1，为过度转向趋势。

值得注意的是，随着内轮转角α的不断变化，轴距系数λ=f（α）也在不断地变化，也就是说，转向程度在不断地变化，转向性质也在变化。在全部转向过程中，只有一个α点，能使λ=1（中性转向）。

λ=1的_α点落在哪里，这对于不同的梯形机构是完全不一样的。设计者的任务就在于合理地选定λ=1的位置，做到与已定轴距的合理匹配。

作为具体的汽车，在轴距L_p和梯形机构已定的情况下，可按下列5个步骤判定它的转向特性。

1.计算无滑移转向的外轮转角

给定一系列的内轮转角α值（前梯形不得大于180°-θ，后梯形不得大于θ），并利用式（6-44）算出相应的无滑移转向（中性转向）的外轮转角值为

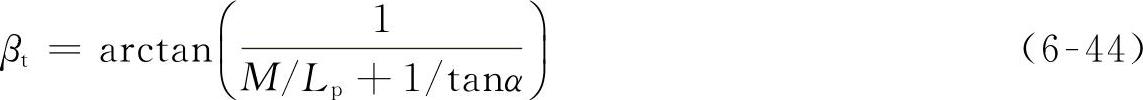
2.计算梯形机构的外轮转角

以上述给定的内轮转角α值，用梯形机构运动学关系得出的式（6-41），计算相应的梯形机构的外轮转角值。

3.确定车轴偏离角

车轴偏离角，是指在给定内轮转角下，实际梯形机构造成的转向角δ_p与无滑移运动的转向角δ_t的差。δ_p与δ_t可由式（6-45）和式（6-46）计算。

所以车轴偏离角为

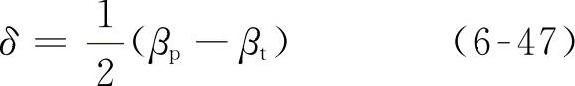
由于后轴没有发生偏离，所以式（6-47）的δ值就是前后轴偏离角差Δ，故可直接用于检验具体梯形机构在不同内轮转角下的转向趋势。

为了更好地观察具体梯形机构的转向性质和转向的变化过程，尚需利用已得的δ值绘制α-δ曲线，如图6-16所示。

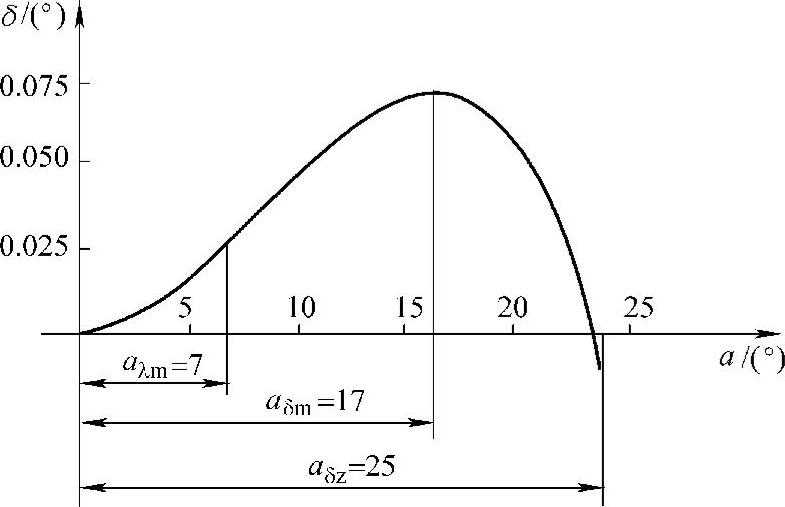
图6-16 α-δ曲线

4.计算无滑移转向轴距和轴距系数

计算无滑移转向轴距和轴距系数是为了考察在转向过程中，具体梯形机构在保证车轮纯滚动下的轴距变化情况。它们能较为直观地显示其转向趋势和转向程度。

无滑移转向轴距可用式（6-48）计算：

式中 L_t——无滑移转向轴距（mm）；

β_p——具体梯形机构的外轮转角（°）。

轴距系数λ可用式（6-43）计算。

为了观察L_t和λ值的变化过程，还应作出α-λ曲线，如图6-17所示。

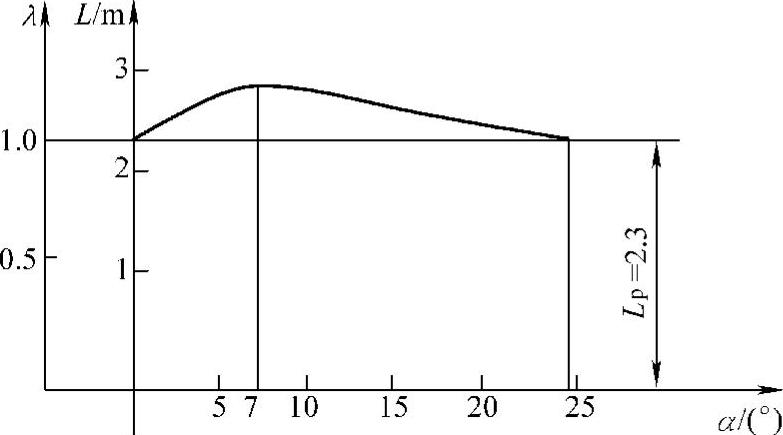
图6-17 α-λ曲线和α-L曲线

5.示例计算与分析

为掌握梯形机构转向特性的规律，特选择了8种梯形机构进行分析计算，其有关参数及其计算结果见表6-5。

在8种梯形机构中，有7种是前梯形。在7种前梯形中，编号为A～F的6种，均与2300mm的轴距匹配，且主销中心距均为1246.8mm，梯形臂皆等于170mm。不同的是，让梯形角θ从120°逐步变到90°。同时，对拉杆n的数值作了相应的调整。编号为G的前梯形是为了进行轴距变化的对比。编号为B'的后梯形则是为了与编号为B的前梯形对比。

为了更好地理解表6-5的计算结果，特将B'号后梯形的部分内轮转角的计算结果列于表6-6之中。

表6-5 不同梯形机构的转向特性

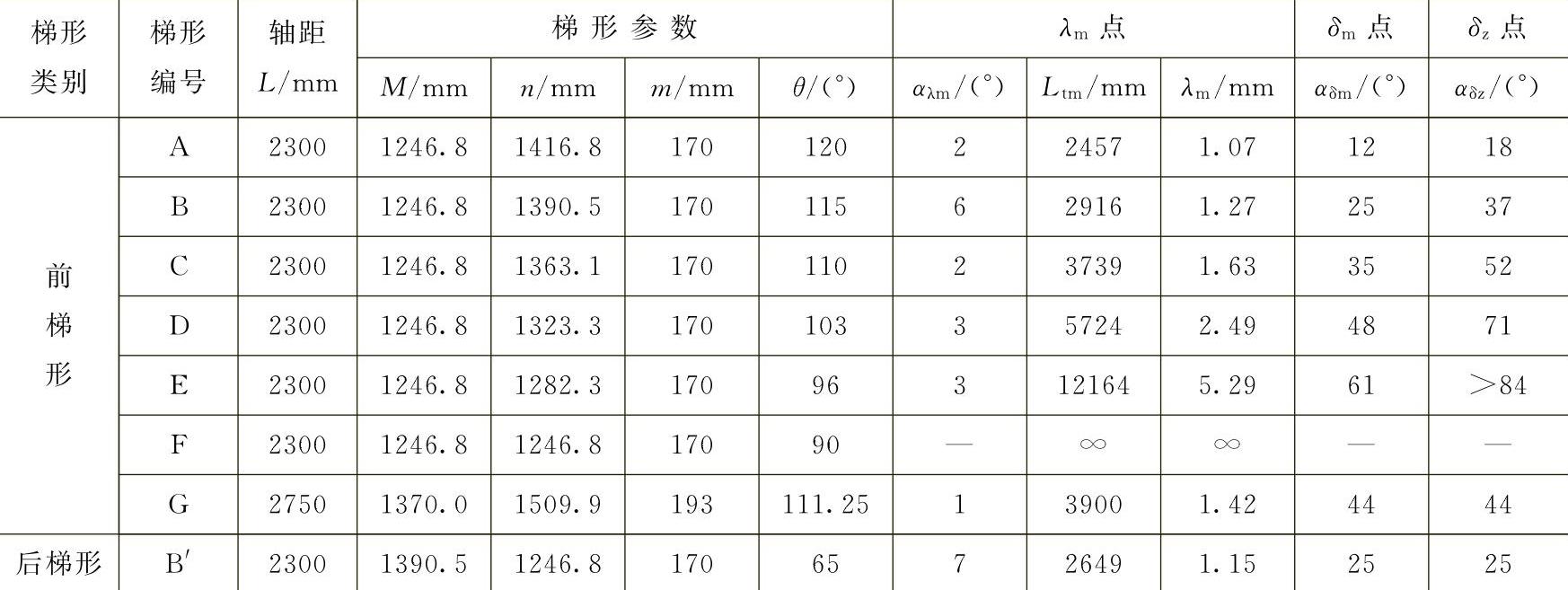
表6-6 B'号梯形机构的匹配特性

从表6-6数据可知，随着内轮转角α的增加，轴偏角δ从小到大，直至α约为17°时达到最大值δ_m，然后又开始减小。当α≈25°时，减至最小值δ_z=0，之后变为负值，且越负越大。也就是说B'后梯形与2300mm轴距匹配所得的转向特性是：

当α在0°～25°的区间内属于不足转向趋势，而17°～25°的区间则是不足转向程度的下降区段；当α≈25°时，为中性转向趋势；α＞25°后则变为过度转向趋势。

作为无滑移转向轴距L_t则是从实际轴距L_p=2300mm开始逐步增大，当α≈7°时达到最大值L_tM=2649mm。此时的轴距系数λ获得最大值λ_m=1.15。之后，L_t值逐步回落。当α≈25°时，L_t=L_p=2300mm，继而逐步减小。

图6-16的α-δ曲线以及图6-17的α-λ曲线清楚地显示了该梯形机构的转向特性。

从表6-5数据可知，B'号后梯形所具有的转向特性，具有普遍意义，所有梯形机构都是在内轮转角α的变化过程中，具有三个关键点：

1）纯滚动轴距和轴距系数获得最大值L_tm和λ_m的点α_λm，该点一般出现在初始转角上。

2）轴偏角获得最大值δ_m的点α_δm，这是不足转向趋势由增到减的转折点。(www.xing528.com)

3）轴偏角降为零值δ_z的点α_δz，这是不足转向与过度转向的转换点，即中性转向点。此时的轴距系数λ=1，纯滚动轴距等于实际轴距，即L_t=L_p。

不同的梯形机构和不同的匹配，会造成：

1）轴距系数的最大值λ_m是随梯形角θ的变化而变化的。θ值越大，λ_m值越小。一般来说，λ_m值在1～∞之间变化。D号前梯形是一个实际采用的方案，而λ_m=2.49。也就是说，轴距变化约两倍半，不足转向程度高，跨越的区间也大。

2）轴偏角的最大值δ_m和零值δ_z也是随θ值的变化而变化的。θ值越大，δ_m和δ_z出现得越早。值得注意的是，δ_m和δ_z所对应的内轮转角α_δm和α_δz的分布还具有一定的规律性。二者的比值，大约在式（6-49）的范围之内。

式（6-49）描述了梯形机构转向特性从量变到质变的内轮转角的变化规律。

3）从表6-5的B号前梯形与B'号后梯形的计算对比可知，前后梯形的转向特性规律没有多大不同，只是后梯形的不足转向下降点和中性转向点出现得更早。

基于上述认识，设计者在选择梯形机构时就有了主动权，改变梯形参数，就可获得不同的最大轴距系数，获得所需的不足转向下降点和中性转向点。

汽车实际的内轮转角使用值一般不超过30°，故中性转向点应大于此点。

以上所讲的是二轴汽车梯形机构的内、外轮转角关系和梯形机构的转向特性。作为三轴以上汽车的梯形机构，其内、外轮转角关系式（6-41）依然适用，然而无滑移转向的外轮转角公式（6-44）却需要另行推导。例如四轴汽车一、二轴转向的情况（图6-8），其外轮转角则应采用式（6-18）和式（6-19）计算。除此之外，与其他梯形机构转向特性分析没有什么区别。

（三）转向机构附加牵动轮转向

转向机构附加牵动轮转向包含两个方面的内容：一是转向系统与悬架机构运动干涉造成的车轮转向；二是垂臂球头中心绕侧倾中心转动带来的车轮转向。这些都和梯形机构相关，下面分别研究。

1.转向系与悬架运动干涉的轮转向

转向系与悬架运动的不协调性，在可逆转向系统中，当车速较低时，往往造成转向盘的摆振；而在不可逆的转向系统中，当车速较高时，必将引起转向车轮的干涉转向。现以图6-18所示的悬架和转向系统为例来研究这个问题。

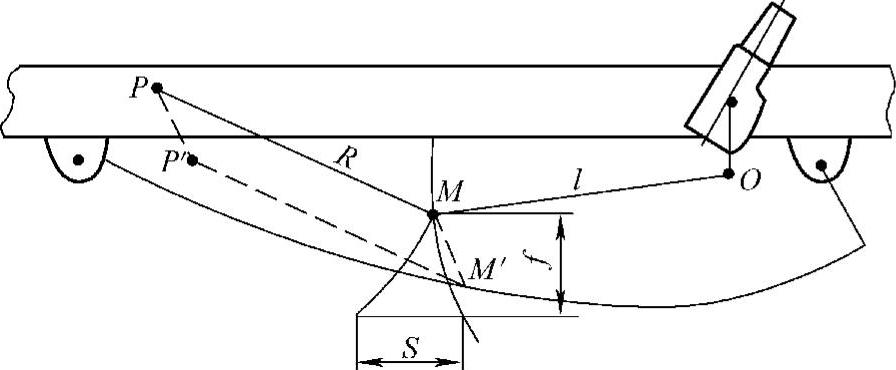
图6-18 悬架与转向系的运动干涉

图6-18系摆耳在后的纵置对称板簧悬架。转向系为转向机在车轴之后的直拉杆式。图中O点为垂臂球头中心，M点为节臂球头中心。当车身上下跳动或者侧倾时，M点既以O点为圆心、以直拉杆长度为半径画弧运动，也以M点的轨迹中心P为圆心、以M点的轨迹半径R为半径画弧运动。二者的矛盾随悬架变化量的大小而变，或者随车身侧倾角的大小而变。

假设悬架的变形量为f，且O点与M点近似地在同一纵向平面内，那么两者运动的矛盾量就是S。在同一悬架变形量的情况下，由于摆耳位置以及O点和M的布置位置不同，矛盾量的大小也将不同，而且压缩和反弹行程也不相同。我们研究和关心的是矛盾量较大的那个行程。

如何统一这个矛盾呢？假设不考虑球头胶件的变形和克服各种间隙，矛盾量S必将转化为转向节臂和车轮的角位移，如图6-19所示。

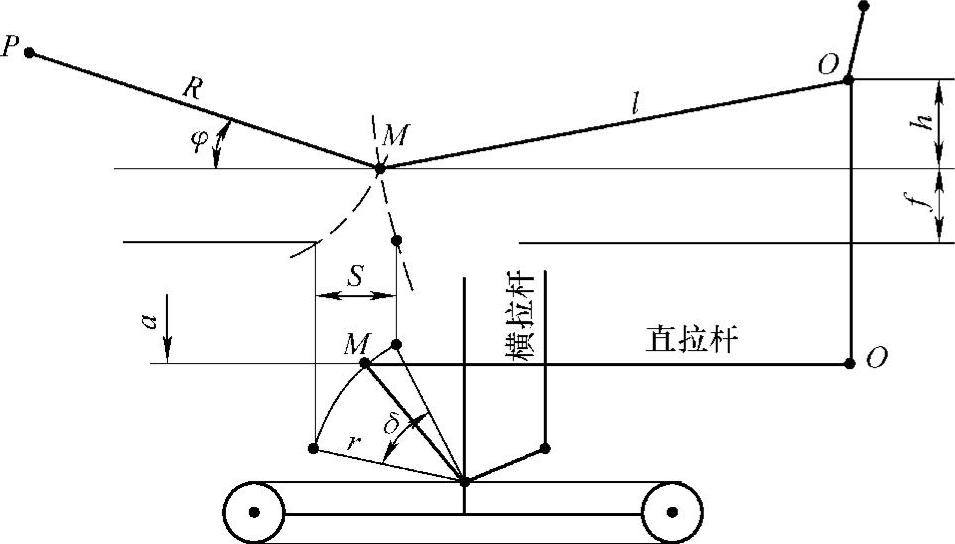
图6-19 水平位移与角位移

根据图6-19的几何关系，水平方向上的矛盾量可由式（6-50）求出：

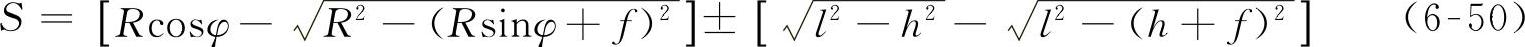
式中 R——节臂球头中心M的轨迹半径（mm）；

φ——悬架推杆角（°）；

l——直拉杆的长度（mm）；

h——l在垂直方向上的长度（mm）；

f——给定悬架的垂直位移（mm）。

f一般以车身在0.4g侧向加速度j的作用下的侧倾角θ来计算：

f=aθ （6-51）

式中 θ——车身侧倾角（rad）；

a——节臂球头中心至车身中心线的距离（mm）。

式（6-50）中的正负号，是由垂臂球头中心O的位置与节臂球头中心M的轨迹中心P的位置来决定的。如果O、P两点在车轴的异侧（图6-18），应取正号，同侧则取负号。由此可知，板簧固定吊耳与转向机同侧布置，可使运动干涉大为降低。

求出了水平方向上的矛盾量，便可由式（6-52）算出车轮偏转角（梯形臂转角）：

式中 δ——车轮偏转角（rad）；

r——节臂长度（mm）。

轴偏角到底反映了什么转向性质呢？假设转向盘内转，车身外倾，图6-19中的O点上提，这相当于M点下移，此时的矛盾量S需要节臂内转来统一，故此转向属于过度转向；反之，若转向盘外转，节臂依然外转，仍属过度转向。假若不打转向盘，只是车身上下跳动，此时必将造成车轮来回摆振，这将使不同转向趋势交替出现。

2.垂臂球头中心侧倾轮转向

汽车转向机构的形式大多数系以纵向上的直拉杆带动转向节臂转动。然而，部分汽车的转向机构却是以横向上的横拉杆带动节臂转动，进而带动梯形臂转动。BJ212越野汽车就属于这种形式，如图6-20所示。

由式（6-52）所求出的车轮偏转角，仅是内轮偏转角，由于此偏转角较小，故可近似认为此轮偏转角就是轴偏角。

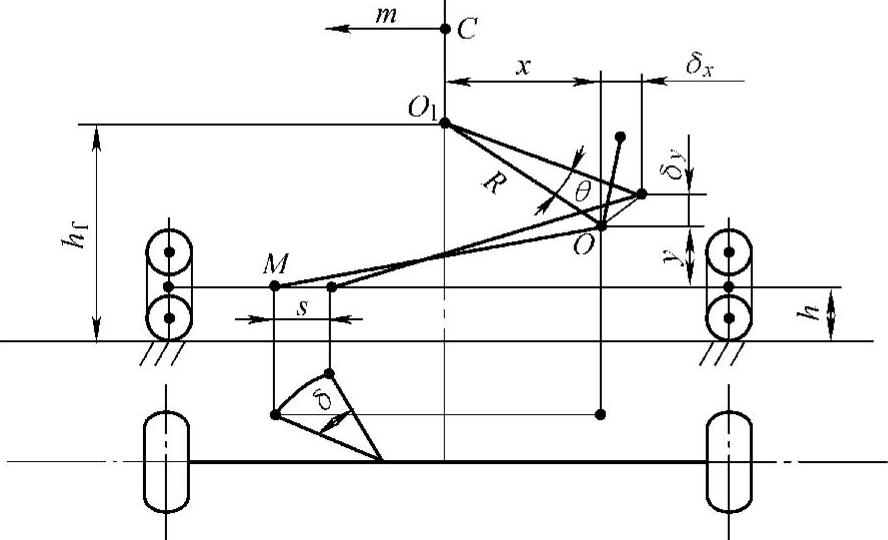
图6-20 转向机构轮转向

【计算示例】 示例车型为燕京YJ620型乘用车。该车前板簧倾角ξ=3°，固定吊耳在前，簧长L=1200mm，采用“柏林式”卷耳，满载弧高F=7mm，夹紧长度d=92mm，转向机与固定吊耳同侧。横拉杆长度l=740mm，垂直方向投影长h=139mm，节臂球头中心至车身中心线的距离a=525mm，节臂长度r=135mm，计算过程如下：

计算推杆长度和推杆角：

R=3（1200-92）/8=415.5mm

φ=arcsin（7/415.5）+3.3°=3.97°

假设车身在0.4g侧向加速度作用下的侧倾角θ=3.5°，那么由式（6-51）便可算出悬架变形量（节臂球头中心相对车身的垂直位移）：

f=525×3.5/57.3=32mm

用式（6-50）计算水平方向上的矛盾量：

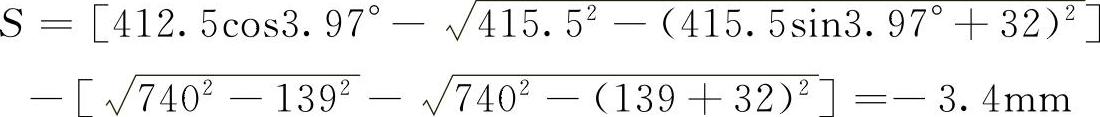
用式（6-52）计算车轮偏转角（梯形臂转角）。

δ=3.4/145=0.0025rad=1.44°

1.44°这个较小的轮偏角，说明该型车的布置方案是较合理的。反之，在同样条件下，如果P、O两点异侧布置，那么水平矛盾量将超过10mm，轮偏角可达4°之多。

式（6-52）所计算的轮偏角，仅是转向机构一侧的车轮偏转角，为简化分析，此处我们就把它当做车轴偏离角。

车身在侧向加速度j的作用下，置于车身上的垂臂球头中心点O便绕侧倾力矩中心O₁转过一个θ角，同时通过横拉杆l带动节臂球头点M横向移动了一个距离S。这个横向位移必然是通过节臂和车轮的偏转来实现的，它可由式（6-53）求出：

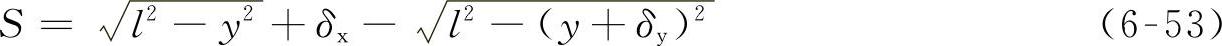
式中 δ_x=R[sin（θ_o+θ）-sinθ_o]；

δ_y=R[cosθ_o-cos（θ_o+θ）]；

θ_o=arcsin（x/R）；

R=；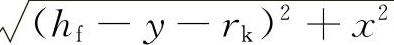

l——横拉杆在横向平面上的长度（mm）；

y——垂臂球头中心点O的坐标（mm）；

h_f——侧倾中心O₁距地面的高度（mm）；

r_k——车轮滚动半径（mm）；

θ_o——O点及O₁点的连线与纵向平面的夹角（°）；

θ——车身侧倾角（°）。

【计算示例】 示例车型有关参数：l=900mm，x=150mm，y=40mm，h_f=550mm，r_k=365mm。节臂长r=145mm。

取侧向加速度j=0.4g时，侧倾角θ=3.5°。由式（6-53）可以计算如下参数：

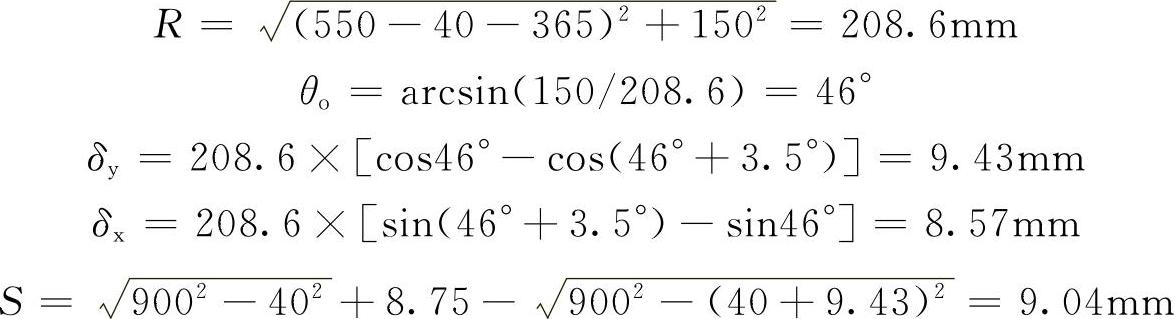
利用式（6-52）计算车轮偏转角：

δ=9.04/145=0.0623rad=3.57°

由图6-20的情况可知，所增δ角是与转弯方向一致的，故属过度转向趋势。

假如在其他条件相同的情况下，使侧倾中心O₁点降低，便可减少车轮偏转角。若使O点低于垂臂球头中心O，那将使过度转向趋势变为不足转向趋势。