多轴汽车转弯半径计算公式

汽车的转弯半径R与汽车的内轮转角α、轴距L、车轮转臂a、主销中心距M等因素有关。汽车的最小转弯半径R_min，则是和汽车最大内轮转角αm相对应的，它是在给定α_m的条件下，汽车以低速转弯时，前外轮与地面接触的轨迹到转向中心点O之间的距离，如图6-4所示。

转弯半径与车轴数紧密相关，不同车轴数的转弯半径有着不同的表达式，下面就以二轴、三轴和四轴为例来建立转弯半径的计算公式。

图6-4 理想的内、外轮转角关系

（一）二轴汽车的转弯半径

在建立转弯半径计算式之前，先研究一下理想的内、外轮转角的关系。

1.内、外轮转角的关系

在转向过程中，为使全部车轮都处于纯滚动而无滑移状态，则要求全部车轮都绕瞬心O作圆周运动。在一般转向条件下，每个车轮的转弯半径都是不同的，同一车轴上的两个转向轮，即内轮和外轮的转向角也是不同的，它们的关系为：

式中 α——内轮转角；

β——外轮转角；

L——轴距；

M——主销中心距。

2.纯滚动转弯半径

在车轮纯滚动的情况下，也就是在理想的内、外轮转角关系的条件下（阿克曼原理），二轴汽车的最小转弯半径为

式中 α——车轮转臂；

β_m——外轮最大转角。

3.梯形机构决定的转弯半径

汽车的转弯半径，严格说来，完全取决于梯形机构，它与轴距的大小基本无关。当梯形机构参数确定后，给定一个内轮转角α，就确定了相应的外轮转角β，有了内、外轮转角α和β，就确定了转向瞬心，即确定了转弯半径，如图6-5所示。图中L_p是实际轴距，L_t是理论上的纯滚动轴距。

在假定没有侧向偏离的情况下，由图6-5的关系，可求出最小转弯半径：

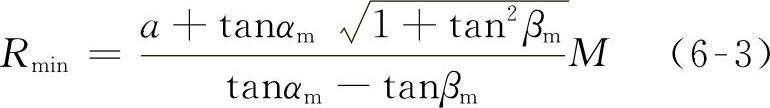
图6-5 梯形机构确定的转弯半径

式中 a——车轮转臂；

M——主销中心距；

α_m、β_m——内、外轮最大转角。

4.二轴全轮转向的转弯半径二轴全轮转向汽车的最小转弯半径可由图6-6的关系求出，即

二轴全轮转向汽车的优点在于提高机动性。由式（6-4）可知，在轴距和外轮转角相等的条件下，其转弯半径要比仅前轮转向的约小一半。然而，外轮转角相同时，在全轮转向的汽车上，内轮就需转过较大的角度，要占用较大的空间。所以，如果转向空间受限制的话，实际最小转弯半径减少就不到一半。全轮转向的另一优点是转弯时的车轮轨迹只有两条，而只前轮转向的汽车则有四条。因此减少了汽车在松软土地上的行驶阻力和所消耗的功率，提高了通过性。全轮转向还会使转向传动装置更为复杂，使转向传动中的总间隙增加，这将影响高速行驶的稳定性。此外，全轮转向的汽车还难于从停车处驶出。为消除这些缺点，在结构中还应考虑装设锁住后轮传动装置的机构。

图6-6 二轴全轮转向汽车的转弯半径

（二）三轴汽车的转弯半径

1.瞬时转向中心

为建立三轴汽车转弯半径的计算式，先假设前轮为转向从动轮，且略去前轮的滚动阻力和惯性力的影响。在考虑侧向偏离的情况下，假定点O为瞬时转向中心，δ_1a、δ_2a、δ_3a分别为前、中、后三轴的侧偏角，如图6-7所示。图中θ为转向轮内外轮α和β的均值，即θ=（α+β）/2。

各轴中点的速度方向由向量v₁、v₂和v₃来决定。轴的侧偏角对于双后轴的车轴决定于v₂和v₃的方向同汽车纵轴线间的角度，而对于前轴，则决定于转向轮平均转角θ和速度v₁方向之间的角度。

由于车轴有侧偏，在车轮上出现了侧向力Y。下面确定瞬时转向中心的实际位置，为此必须找出偏侧角δ_1a和δ_2a。根据作用于汽车上力的平衡条件，可以写出

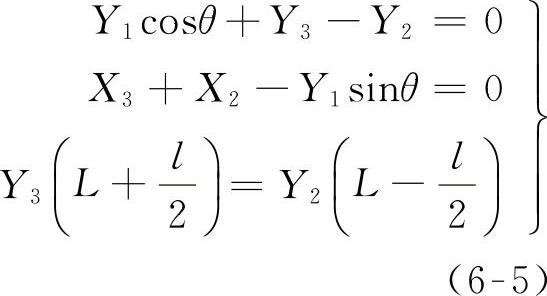
在式（6-5）中，包含四个未知数（Y₁、Y₂、Y₃和ΣX=X₂+X₃），考虑到所求的未知数R_o和C（决定转向中心的位置），必须还要三个方程式，为此可利用下列几何关系：

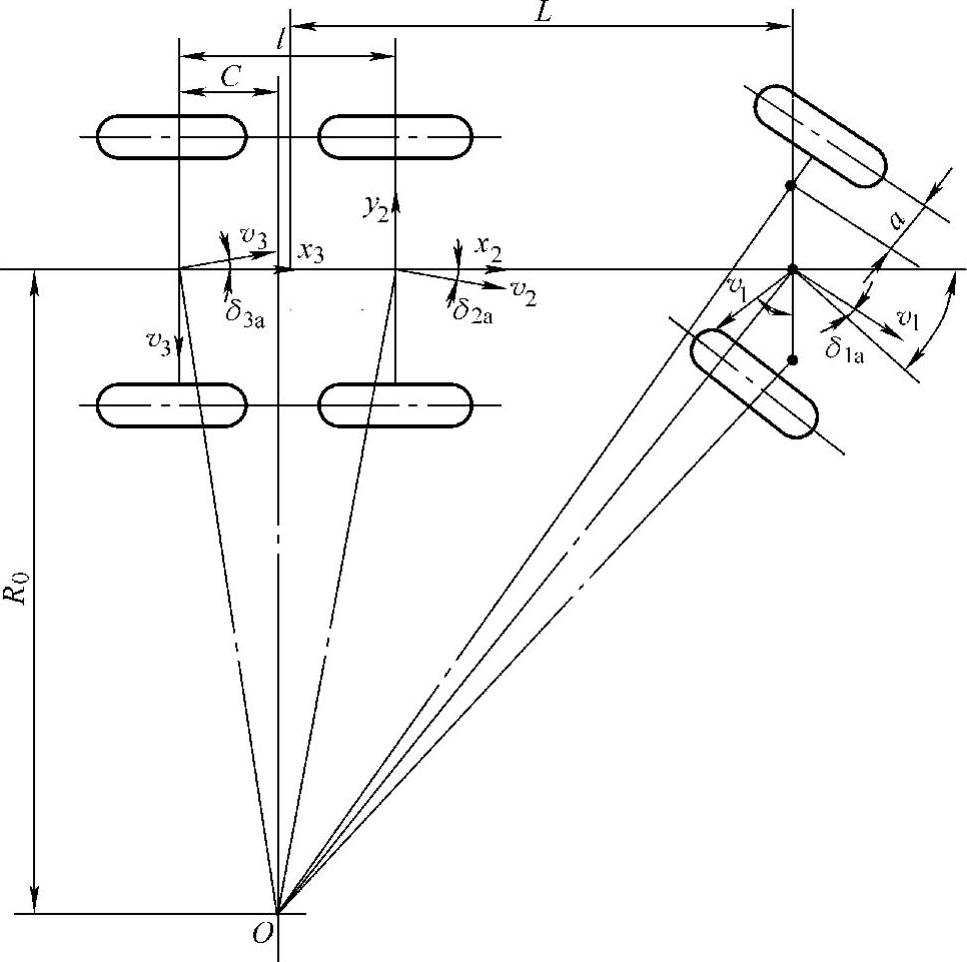
图6-7 前轴转向的三轴汽车

侧向力与侧偏角有下列关系：

式中，K₁、K₂和K₃是相应车轴上的车轮侧偏系数。

解式（6-5）～式（6-7），可求出瞬时转向中心：

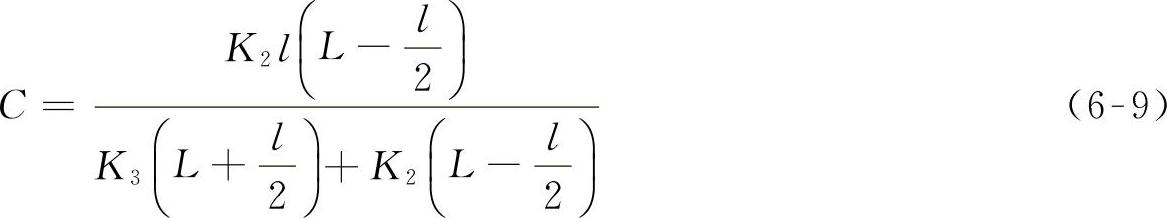
在许多情况下，可认为K₁=K₂=K₃，则式（6-8）和式（6-9）可写成：

从式（6-11）可见，在给定的行驶条件（低速）下，三轴汽车的转向中心总是相对双后轴中心线往后移，并且双后轴的轴距越大，后移也越多。

2.三轴汽车的最小转弯半径

在已知转向中心位置的情况下，可直接求得三轴汽车的最小转弯半径，即

式中 M——主销中心距；

β_m——外轮最大转角。

为了理论分析的需要，还可将三轴汽车的最小转弯半径表达为：

将C值代入式（6-13）得到：

式（6-14）中的δ_1a可以用式（6-6）、式（6-10）和式（6-11）求出。

比较式（6-14）和式（6-2），可以得到如下结论：三轴汽车的最小转弯半径总是大于同样轴距的两轴汽车的最小转弯半径。首先，这是由于瞬时转向中心向后移了，其次，三轴汽车甚至在低速行驶时也存在着前轮侧偏的现象。转弯半径的增加主要取决于双后轴的轴距，它在公式的分子中是二次方，与此同时，车轮的侧偏角，包括前轮的侧偏角要显著增加，因此转弯半径也增加。

如果三轴汽车转弯速度较大，不能忽略侧向惯性力的作用时，转向运动特点就取决于侧向惯性力所引起的各车轮侧偏角变化的情况。由于侧向惯性力的作用，在所有车轮上产生了向心的侧向反作用力，在前轴和后轴上，上述侧向反力与忽略侧向惯性力作用时汽车转向所产生的反力相叠加（图6-7），而在中轴的车轮上，两种反力是相减的，由于这个原因，前轴和后轴车轮的侧偏角随着速度的增加而增大。而中轴车轮的侧偏角则减小，到某一速度后，改变符号，此时C值应考虑侧向惯性力作用的影响，和两轴汽车一样，取决于后轮侧偏角，根据侧偏角的变化，车速越高则三轴汽车瞬时转弯中心向前移得越多。此时最小转弯半径既取决于C的数值，又决定于δ_1a角，见式（6-13）。

将三轴汽车的前驱动轴接通，则会对转向运动产生和两轴汽车上相同的变化。

从保证三轴汽车具有最好的转向运动关系的观点出发，应该使中轴和后轴尽量接近。可是在目前的许多设计中，为了提高通过性，改善重量在轴间的分配，常把中轴设置在前轴和后轴的中间。如果此时只有一个轴的车轮是转向轮，则转弯阻力和转弯时轮胎的磨损将由于所有车轮侧偏角的显著增加而大大增加。所以，这种类型的三轴汽车通常是双轴转向的，在有的汽车上采用了前、中轴转向。但是这种汽车的最小转弯半径不仅不小于一般的三轴汽车，甚至还略大一些。这是由于前、中轴转向汽车的转弯中心，在低速行驶时处在后轴的延长线上，而前轴转向的三轴汽车的转向中心相对后轴向前移了。

等轴距的三轴汽车也有做成前、后轴转向的，这样能改善汽车的机动性，使最小转弯半径比上述几种形式减少将近一半。但实际上内轮转角会受转向空间的限制，最小转弯半径减少不到一半。

（三）四轴汽车的转弯半径

四轴汽车的转向形式，有双前轴转向，前、后轴转向和全轮转向等几种形式。

下面分别研究一、二轴转向和一、四轴转向的情况。首先研究具有双前轴转向的四轴汽车的转向运动学。

1.一、二轴转向的理想转弯半径

所谓理想转向，就是轮胎没有侧向偏离的纯滚动转向。由图6-8的关系，可得四轴汽车一、二轴转向的最小理想转弯半径为(www.xing528.com)

图6-8 一、二轴转向的理想转弯关系

要保证式（6-15）成立，须在假定α₁、α₂为一、二轴内轮转角，β₁、β₂为一、二轴外轮转角的情况下，保证下列关系成立：

2.一、二轴转向的实际转弯半径

所谓实际转弯半径，是指在考虑轮胎侧向偏离情况下的转弯半径，如图6-9所示。

为了简化分析先作如下假定：

1）所有车轴等距分布，且轴距为l。

2）所有车轮侧偏系数相同。

3）转向轮不是驱动轮，且其滚动阻力可以忽略不计。

4）转向速度低而均匀，因此侧向惯性力很小，不影响转向运动学。

图6-9 双前轴转向的四轴汽车

设图6-9中的瞬时转向中心位于点O。要获得点O距后轴中心的距离C和半径R_o，必须列出转弯时，作用于汽车上的力和力矩平衡方程式：

式中 Y_i——车轮侧向力；

θ_i——转向轴的均值转角。

这些方程式中包含了五个未知数Y₁、Y₂、Y₃、Y₄和（X₃+X₄）。为了求得转弯中心的坐标R_o和C，必须再建立四个方程式，为此可以利用下面的几何关系：

式中 δ_1a——车轮侧偏角。

侧偏角和侧向力之间有下列关系：

利用式（6-22）求解式（6-20）和（6-21），从中求出R_o和C值：

由式（6-23）和式（6-24）可知，转弯中心的位置决定于θ₁和θ₂角之比。通常四轴汽车的转向系的设计思路是使所有转向轮的轴线相交于双后轴之间。计算表明，在这种情况下C≈（0.3～0.35）l，即转向中心偏向第四轴。

最小转弯半径可按下列式计算：

式中的δ_1a可通过式（6-21）、式（6-23）和式（6-24）求出。

四轴汽车的最小转弯半径，大致上和一个轴距等于3l的双轴汽车相同。

由图6-9可见，当转向轮像图上那样分布时，由于转弯中心相对于双后轴中心线有所偏移，车轮将走出8条轮辙，这就增加了在松软土壤上的转向阻力，消耗功率较多，并使汽车通过性变坏。

例如：上述四轴汽车是全轮驱动的，则转向轮上的切向驱动力会对转向运动学产生与两轴汽车和三轴汽车相同的影响。当转向的速度达到不能忽略侧向惯性力的情况下，则必须考虑这个力所引起的附加侧偏，这将永远使转向中心前移，而转弯半径则根据后轴和前轴侧偏角之比，可能减小或增大。

当四轴汽车轴距均布时，转弯时在第三轴和第四轴的车轮上将产生显著的侧向力，因此，三、四轴的靠近能使侧向力减小。但对于提高通过性，即对于改善汽车克服水平障碍（壕沟等）而言，将更有利于减小第二轴和第三轴之间的距离。此时，将第一轴和第四轴的车轮做成转向轮比较有利。

图6-10 前、后轴转向的四轴汽车

3.一、四轴转向的转弯半径

一、四轴转向的四轴汽车（图6-10），它的主要优点是在转弯行驶时总共只走出4条轮辙，其结果是在松软土壤上的转向阻力比双前轴转向汽车的要小，转弯时实际上不引起功率循环，这个情况也有助于减少转弯阻力，所以不仅改善了汽车的通过性，也提高了转向机动性。

其转向运动学，采取和上述相同的一些假设。为了求出坐标C和R_o，先列出汽车转弯时作用在汽车上的力和力矩方程式：

式中 l——二、三轴间的距离；

l₁——第一、二轴和第三、四轴间的距离。

利用下列的几何关系，又能得到附加的四个方程式：

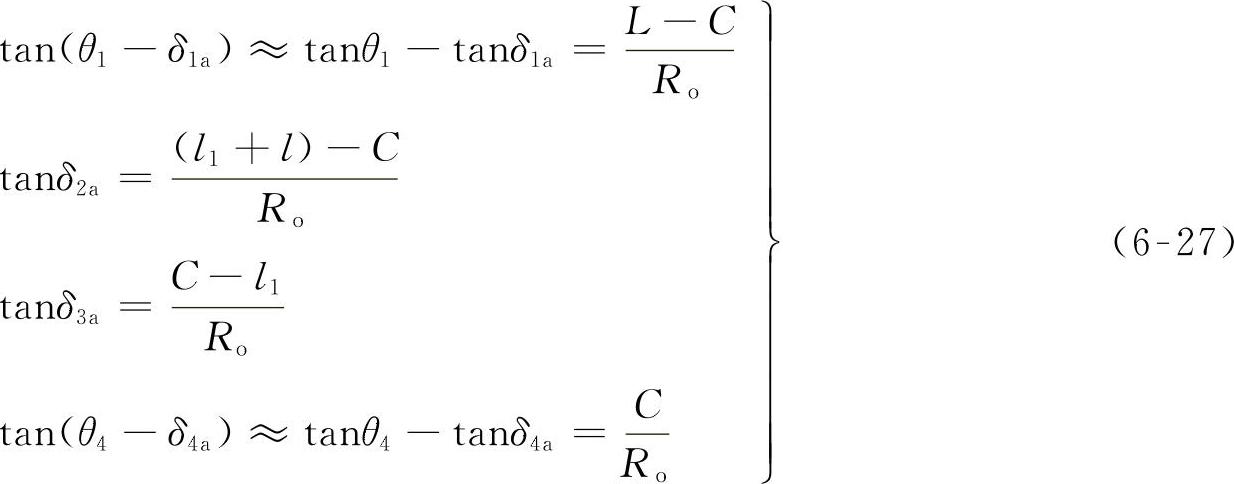
式中 L——首尾两轴之间的距离。

通常θ₁=θ₄=θ

从式（6-22）、式（6-26）和式（6-27）中解出C和R_o，则

最小转弯半径为

式（6-30）中的侧偏角δ_1a按照式（6-27）和式（6-29）确定：

由式（6-31）可见，最小转弯半径在很大程度上取决于二、三轴之间的距离l，它越小，δ_1a也越小，则最小转弯半径R_min也越小，同时，转弯时的侧向力也减少，因而转弯阻力也减少。

如果转向轮同时是驱动轮，则由于前、后两端车轮侧偏角绝对值的减小，最小转弯半径也略为减小，而汽车则有过度转向的趋势。

（四）汽车列车的转弯半径

汽车列车的转向轨迹如图6-11所示。它是在不计轮胎侧偏角的情况下，牵引车前轮转角最大时，前外轮的中心到瞬时转向中心的距离。由该图可知，汽车列车的理论最小转弯半径与牵引车本身的最小转弯半径是相同的，即

图6-11 汽车列车的转向轨迹

实际上，由于牵引车和挂车轮胎的侧向偏离，汽车列车的转弯半径瞬时转向中心并不在同一点上，如图6-2和图6-11所示。当牵引车为二轴汽车、轴距为L₁、前轴主销中心距为M时，考虑轮胎弹性偏离时的列车最小转弯半径为

式中 δ₁、δ₂——牵引车前、后轴内、外轮偏离角的均值（°）；

θ_m——牵引车前轴内、外轮最大转角的均值（°）；

β_m——牵引车前轴外轮最大转角（°）；

δ_o——牵引车前轴外轮轮胎的侧偏角（°）；

L₁——牵引车的轴距（m）；

M——牵引车前转向轴主销中心距（m）；

a——牵引车转向轴车轮转臂（m）。

汽车列车的最小转弯半径和半挂车的位置也可用作图法求得。首先，由牵引车转向时，向各车轮中心平面作垂线，它们的交点便是其瞬时转向中心O。对半挂车来说，其后轴中心线的延长线与转向中心的交点应与半挂车的纵轴线垂直。因此，可以将半挂车牵引销中心O₁与转向中心O连接起来，并以其作为直径画一个半圆（因为半圆上的圆周角总是直角），另以牵引销中心为圆心、以半挂车轴距L₂为半径画圆弧，它与前一个半圆的交点，便是半挂车后轴的中心O₂。这样半挂车的位置也就确定了，如图6-11所示。