轮式车辆在地面上行驶是靠驱动车轮对地面作用获得的地面推进力Fx,当推进力足以克服阻力时,车辆才能运动。该推进力是由于松软地面受到驱动车轮作用时发生水平向后变形产生向前的反力。当发动机给驱动轮提供足够大的驱动转矩时,地面推进力随着土壤变形的增大而增大;土壤的变形导致车轮发生一定滑转,造成车轮(车辆)的速度损失;当地面(土壤)的变形到某一定程度时,地面反力即地面推进力达到最大,超过该变形时,地面反力开始减小;当土壤被完全剪切破坏,该力消失,车轮发生原地滑转,即陷车。本节将根据土壤的剪切力与变形的关系,讨论土壤推进力的计算。
1.土壤最大推进力
前面曾描述了土壤剪切强度τ=c+σtanϕ,或土壤最大剪切应力τmax=c+σtanϕ。由此可知车辆可获得的最大推进力为
Ftmax=τmax=A(c+σtanϕ)=Ac+Wtanϕ (5-62)
式中 A——车辆行走机构与土壤的接触面积;
W——行走机构对地面的垂直载荷;
c——内聚力;
ϕ——内摩擦角。
依据式(5-62),讨论如下:
1)推进力Ftmax由两部分组成:一部分由土壤内聚力产生,该部分仅与车轮接地面积有关,且与之成正比关系;另一部分由土壤内摩擦产生,该部分仅与车辆作用于车轮的垂直载荷有关,且与之成正比关系。
2)饱和粘土的内摩擦角ϕ=0,有Ftmax=Ac。这表明,在内摩擦角ϕ为0或内摩擦角很小的粘性土壤中,增加行走机构接地面积可以提高最大推进力,而与增加车的重量几乎无关。
3)纯干砂的内聚力c=0,有Ftmax=Wtanϕ。这表明,在内聚力c为0的干砂或内聚力很小的摩擦性土壤中,增加车的重量可以有效地提高最大推进力,而与增加接地面积几乎无关。要注意的是,这里讨论的是“最大推进力”而不是挂钩牵引力(车轮的净推力)的问题。在砂性土壤中,增加车的重量固然可以提高最大推进力,但同时还会增加轮胎的沉陷和土壤阻力,有可能减小车轮的净推力。
4)对一般土壤来说,既不是纯粘性也不是纯摩擦性。将式(5-62)两端除以车的重量W,有
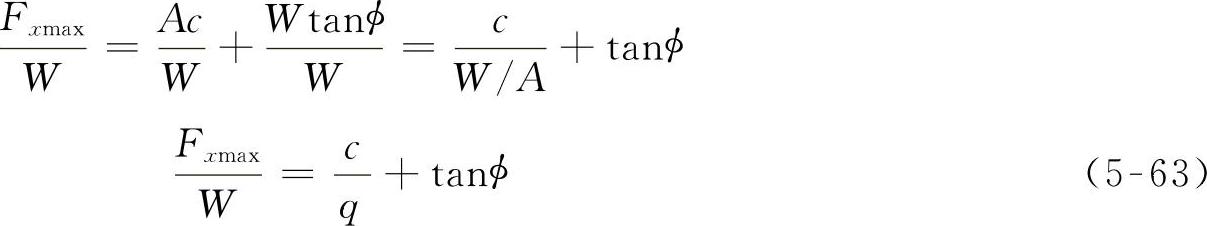
上式表明,要提高单位车重的土壤最大推进力应降低行走机构(轮胎、履带)对土壤的压应力,即接地比压力q。
以上所讨论的公式,仅适用于最大推进力的预测。在达到最大推进力之前的一般工况下的推进力,须在土壤剪切应力-变形规律的基础上进行研究。
 (https://www.xing528.com)
(https://www.xing528.com)
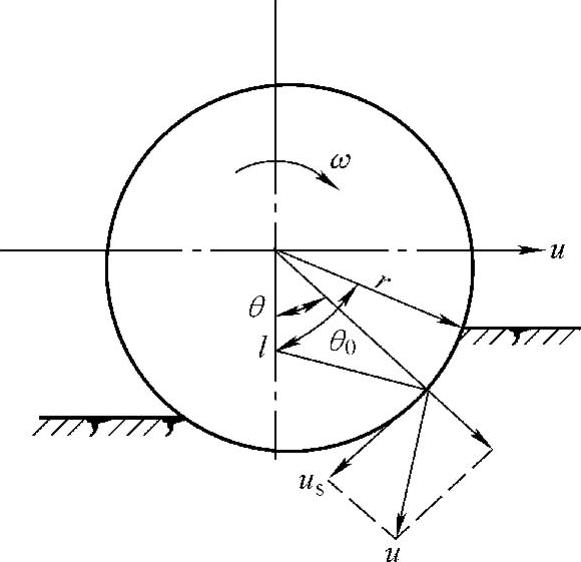
图5-27 刚性驱动车轮受力
2.刚性车轮推进力
在研究车轮对土壤的剪切作用时,要先确定车轮对土壤的剪切位移,如图5-27所示。
设轮缘上任意一点绝对速度沿切向的分量为us,即轮缘上任意一点对土壤的剪切速度。us为该点相对轮心的速度rw和轮心的速度分量uacosθ之和。由于ua=ut(1-sr),故有
us=rω[1-(1-sr)cosθ] (5-64)
设车轮入土角为θ0,转至θ时,车轮转过弧长为s,经历时间为t,在滑转率为sr时,土壤位移为j,有
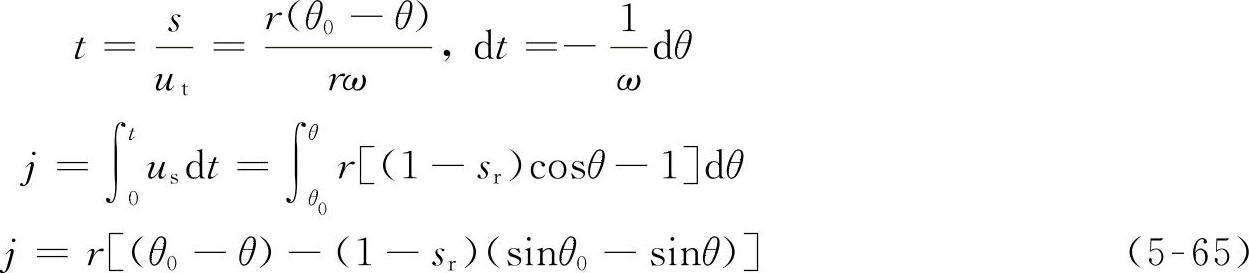
式(5-65)表明,在轮缘各点处的土壤剪切位移不同,该位移为θ的函数。将式(5-65)代入渐进型土壤剪切模型,在轮缘的切应力分布为
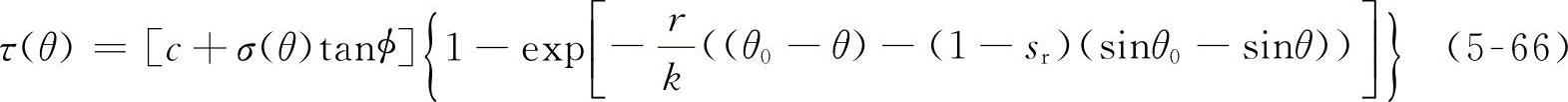
式中 σ(θ)——为法向应力,可用Bekker承压公式计算,其深度为
z=r(cosθ-cosθ0) (5-67)
故
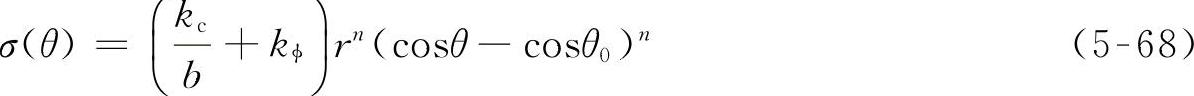
对整个车轮与土壤接触面上切向应力的水平分力积分,即为土壤推进力。
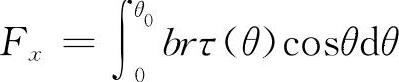
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




