多轴汽车充气轮胎的土壤阻力成果

1.弹性轮胎在松软地面的运动阻力及最佳轮胎气压

一般情况下，弹性轮胎在松软地面滚动，轮胎和地面都发生变形，此时，除了压实土壤阻力F_rc外，还存在轮胎本身的弹性变形引起的阻力F_rs。两种变形阻力都存在于垂直地面方向，在变形中消耗着轮胎从发动机所获得的输入功率。按行驶距离折算的力之和为

F_f=F_rc+F_rs （5-53）

（1）压实土壤阻力 压实土壤阻力F_rc的近似计算方法如下：即认为形成车辙后的土壤表面压力q与轮胎气压P_i及刚度P_c之和相等，轮胎的载荷W完全由轮胎变形时的扁平部分承受，有

式中 L——接触平面部分的长度。

根据Bekker土壤承压公式，有

将式（5-56）代入式（5-48），得

（2）轮胎变形滚动阻力 Bekker对轮胎变形滚动阻力提出的经验公式为

F_rs=uWP_i^-α （5-58）

式中 u、α——与帘布层数、胎壁厚度、轮胎材料、花纹形式等有关的试验系数。(www.xing528.com)

求得u、α方法如下。让轮胎在水平坚实的良好路面如水泥路、钢板飞机跑道上滚动，忽略地面变形阻力。进行上述试验所测得的滚动阻力可认为仅有轮胎变形阻力F_rs。

对式（5-58）取对数，有

logF_rs=（logu+logW）-αlogP_i （5-59）

对于同一型号轮胎，u、α为常数。若取载荷为W不变而改变充气压力P_i，在双对数坐标图上，上式为一条直线；其截距为（logu+logW），斜率为-α。由于W已知，由截距值可得u值。

由压实土壤和轮胎变形的阻力为

2.轮胎最佳充气压力

式（5-60）中的第一项为轮胎压实土壤阻力，由式中可以看出，充气压力P_i增高，则压实土壤阻力增大；第二项为轮胎变形阻力，充气压力P_i增高，则轮胎变形阻力减小。由此可知，必然存在某一轮胎气压P_i0，在特定的松软地面，轮胎的压实土壤阻力与轮胎变形阻力之和将最小。此气压为最佳轮胎充气压力。为此，对式（5-57）求导，并令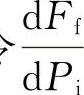=0，有

由式（5-61）求得的最佳气压值P_i0是对应于特定的载荷与土壤条件下，轮胎有最小的阻力。显然，汽车前后车轮的载荷不同，后轮与前轮压过的土壤条件不同，其最佳气压也不会相同。

从以上介绍与讨论中可以得知，具有相同或相近的承载能力，或有相同或相近的接地面积时，大直径、窄断面轮胎的压实土壤阻力和推土阻力要小于小直径、宽断面的轮胎；在特定的松软地面，存在某最佳轮胎充气压力使轮胎的压实土壤阻力与轮胎变形阻力之和最小。