多轴汽车六个接触压力模型和一个数值模型简介

新发展的模型包括六个不同的接触压力模型和一个数值模型。

接地压力模型是基于土壤的承载理论，通过引入平均接地面积，来导出简单的公式。由于计算平均接地面积的方法不同，从而产生了不同的模型。接地面积计算的目的不是要得到一个真实的接地压力，而是要了解轮胎的参数对接地压力的影响，从而进一步导出接地压力与VCI₁的关系。数值型模型的主要思路为导出一个与基本的轮胎尺寸有关的数值，并和VCI₁建立起对应的关系。

这里需要强调VCI₁的物理意义。VCI₁是指一片具有特性一致性的土壤，典型车辆在该土壤上有较高的沉陷和较大的阻力，承载能力的因素比牵引力更加重要。任何人都会想到接地压力起着重要的作用。

1.CP1模型

第一个接地压力模型为CP1模型。CP1与轮胎接地的宽度（WCA）和长度（LCA）有关，参见式（5-21）和图5-5。

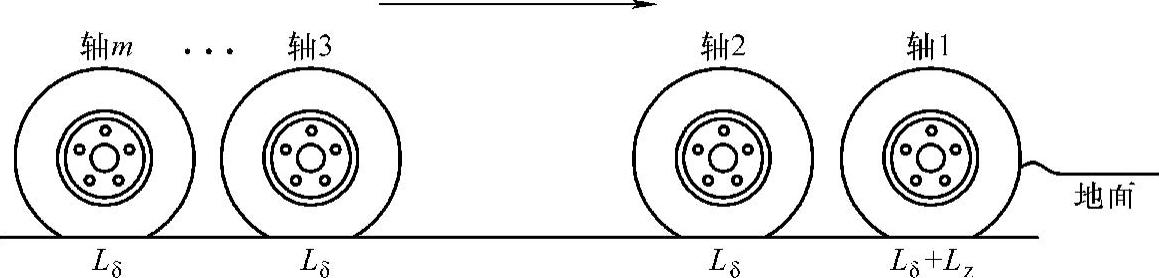
图5-5 平均接地压力参数CP1

从图5-5可以看出，假定有效的接地宽度为轮胎的宽度，每一个轴的接地长度为硬地面接地长度L_δ加上由于轮胎前端下沉造成的附加的一段接地长度L_z。这样，

W_CA=b，LCA=Lδ+1/mL_zCP1=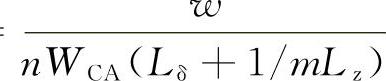 （5-22）

由图5-6可以看出，若δ为变形量，d为轮胎直径，那么

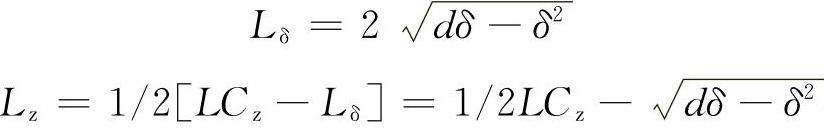
其中，当z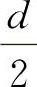＜-δ时，LC_z=2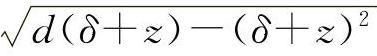；当z≥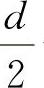-δ时，LC_z=d。

人们对CP1与VCI₁关系进行了许多的尝试，得出以下结果：VCI₁=β₀+β₁CP1＇₁₉+β₂TCF

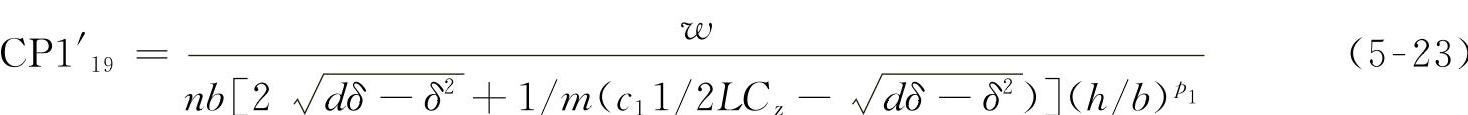
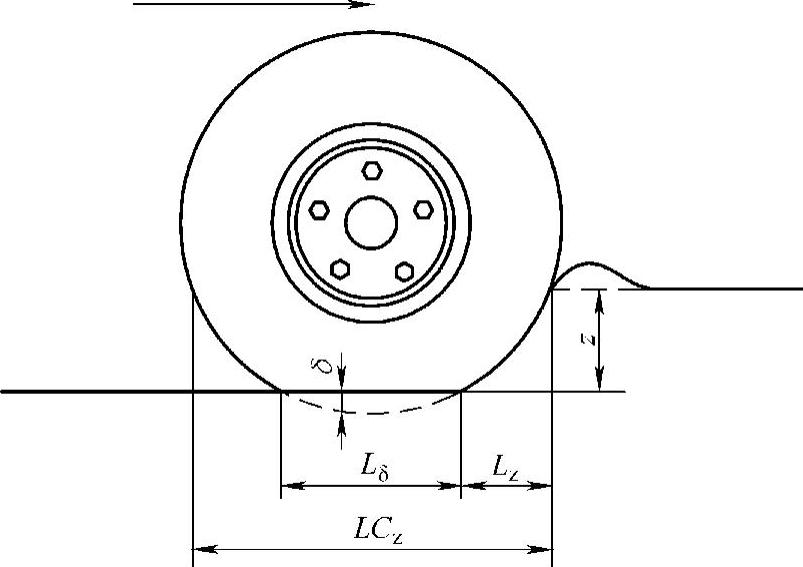
图5-6 接触长度的计算方法

式中，当h_c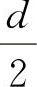＜-δ时，LC_z=2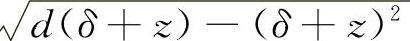；当h_c≥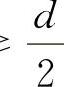-δ时，LC_z=d；

TCF=CTCF，子午线轮胎为0，斜交胎为1。

经过优化后，c₁为0.74，p₁为-0.47。最后结果为

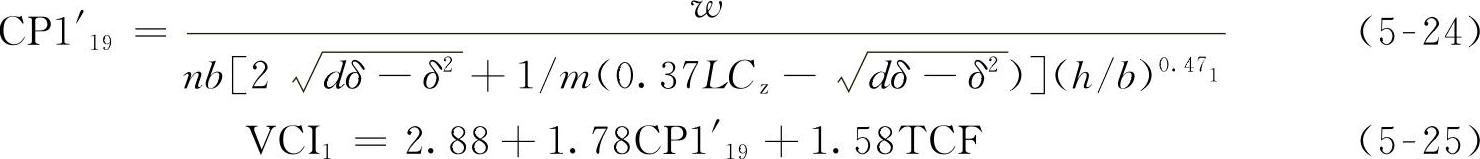
图5-7所示为拟合的结果。

2.CP2模型

接地压力方法的第二个模型为CP2模型。CP2的计算与CP1一样，仍然使用轮胎的有效接地面积。

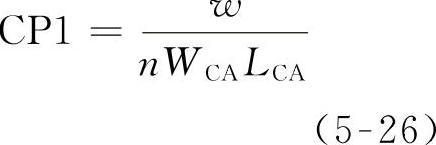
从图5-8中可以看出，假定有效的接地宽度为轮胎的宽度，每一个轴的接地长度为硬地面接地长度为L_δ+c，由硬地面的轮胎变形加上一个经验的修正系数c，这样W_CA=b，L_CA=L_δ+c。

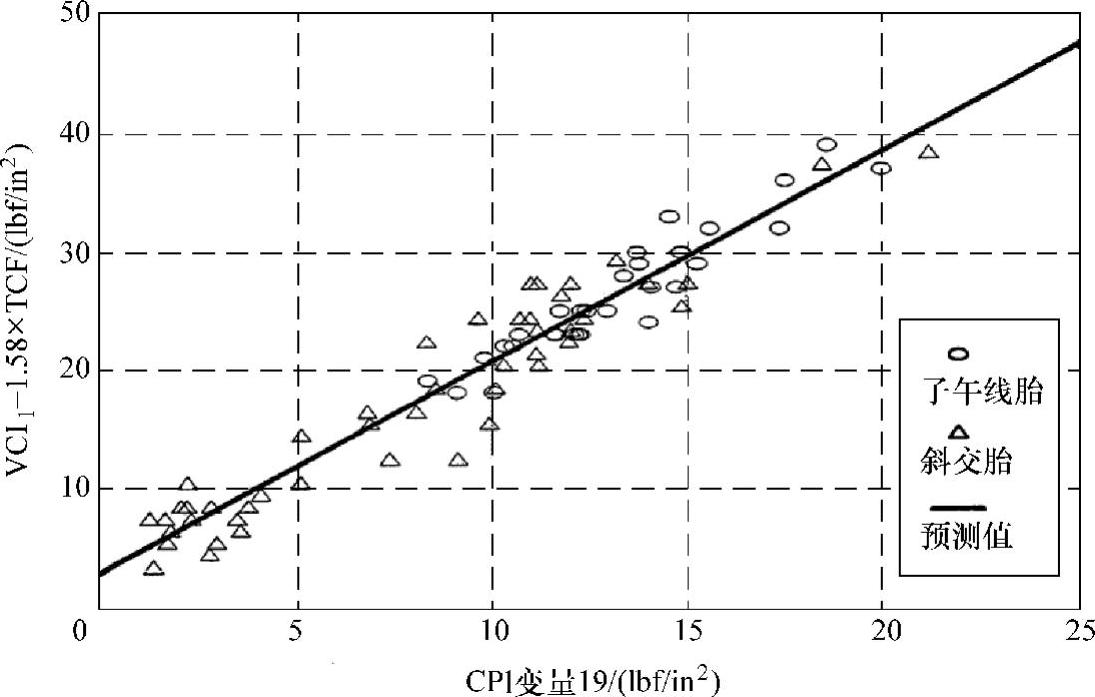
图5-7 CP1与VCI₁拟合结果(www.xing528.com)

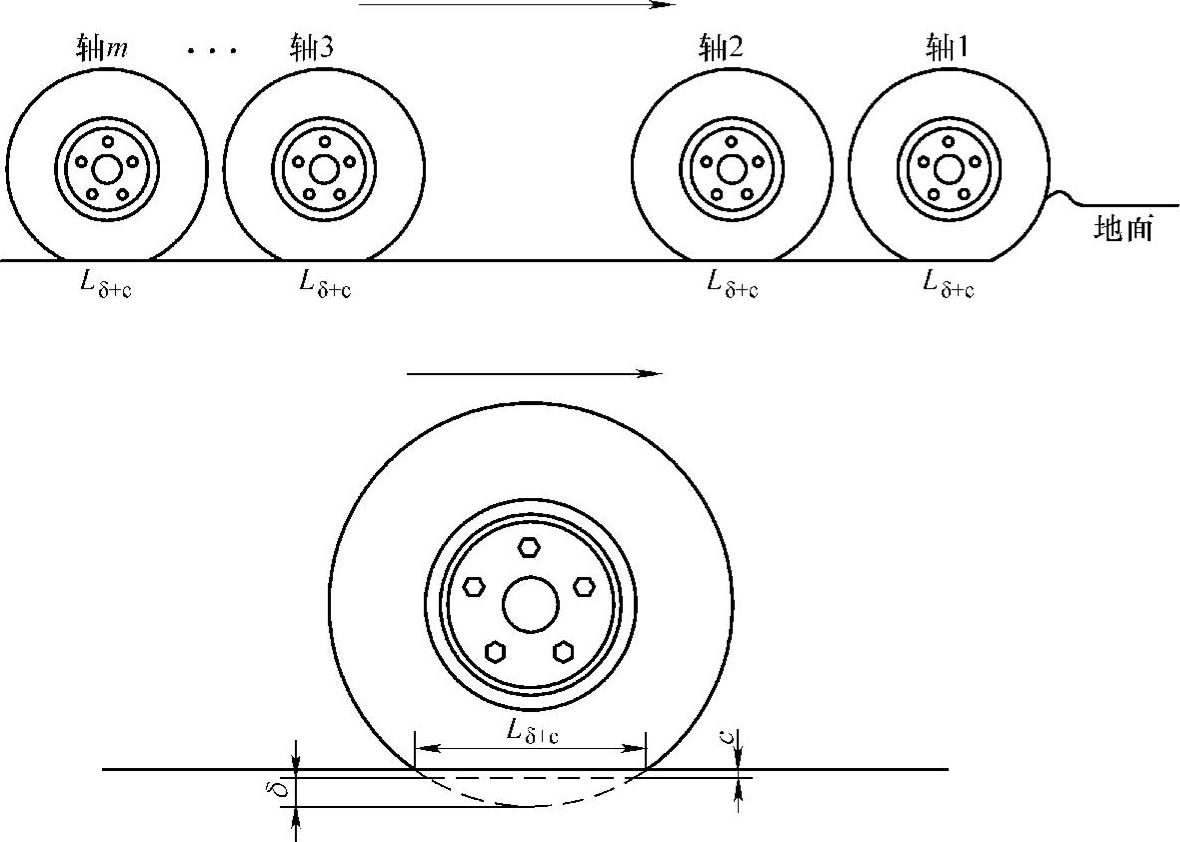
图5-8 轮胎有效接地面积的计算

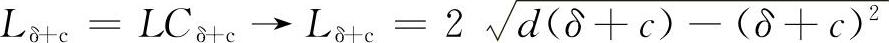
人们对CP2与VCI₁关系进行了许多的尝试，得到以下结果：VCI₁=β₀+β₁CP2'1+β₂TCF

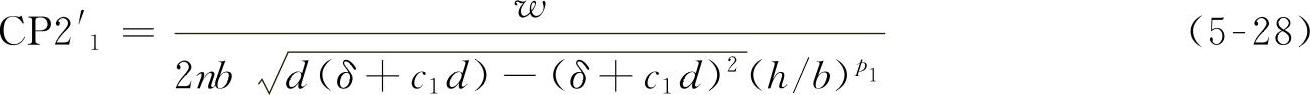
TCF=CTCF，子午线轮胎为0，斜交胎为1。

通过优化后，c₁为0.026，p₁为-0.52。最后结果为

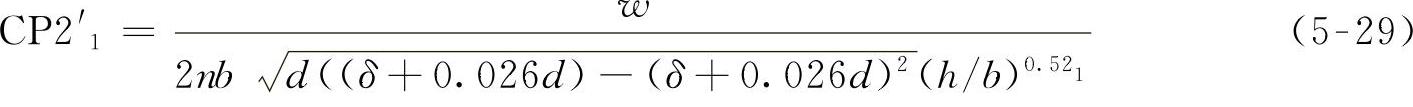
VCI₁=1.95+2.03CP2'₁+1.95TCF（5-30）

图5-9所示为拟合结果。

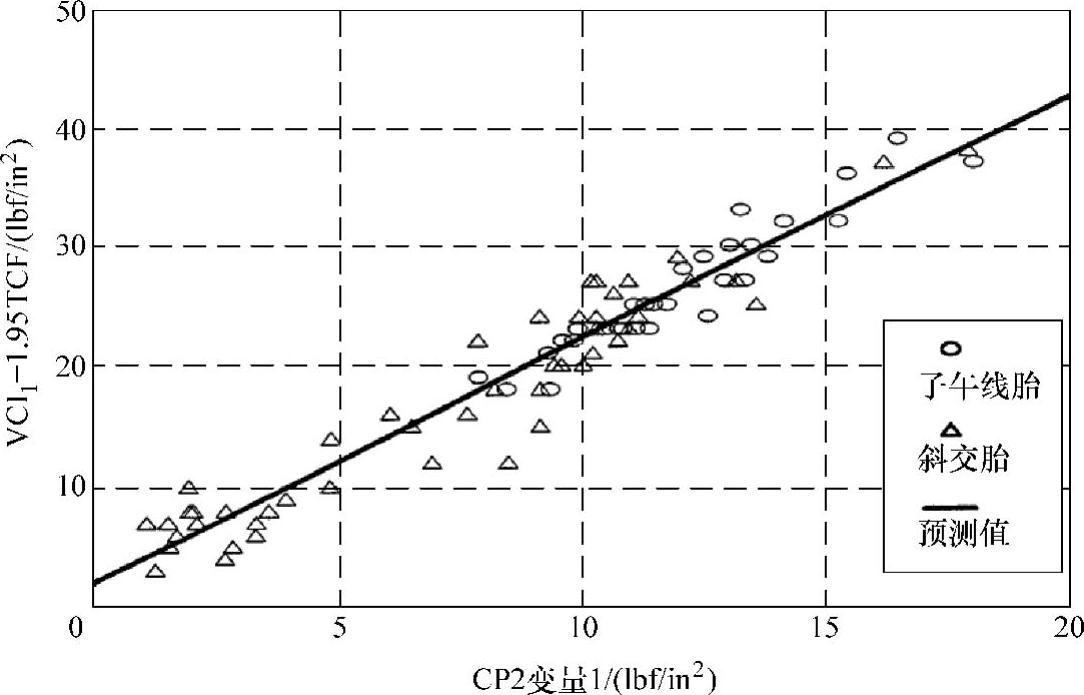
图5-9 CP2与VCI₁拟合结果

3.数值模型

这一模型中引入了变量N_3b，它是控制VCI₁的主要参数，其表达式如下：

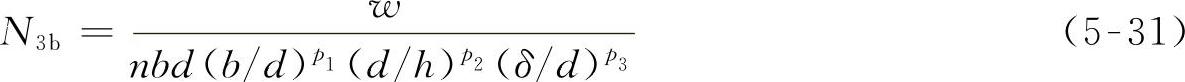
式中 b——轮胎断面的平均宽度；

n——平均每个桥上的轮胎数量；

d——轮胎外侧的平均直径（充气非加载状态）；

δ——硬地面轮胎侧偏量；

h——轮胎平均端面高度。

在N_3b变量中，w/n是一个基本的参数，单位为力的单位。面积的单位由b和d的乘积获得。还采用了三个无量纲的单位和相应的指数（p₁，p₂，p₃）。这样主要的轮胎参数在公式中得到体现。TCF参数被用来考虑子午线和斜交胎的影响。公式如下：

VCI₁=β₀+β₁N_3b+β₂TCF （5-32）

经过一系列变换后，可直接得到式（5-29）～式（5-31）。

TCF=cTCF，子午线轮胎cTCF=0，斜交轮胎cTCF=1。

通过线性拟合和优化后得到p₁=0.42，p₂=0.66，p₃=0.32。代入上式后，得

VCI₁=1.56+2.03N_3b+2.03TCF （5-34）

数据拟合结果如图5-10所示。