中间轴偏离中性面，阻力系数与阻尼比的要求

1.倾角公式

由式（3-68）可知，车身倾角除随簧载负荷P增大外，还有许多影响它的相关因素：

1）加速度。纵、横向加速度j越大，车身最大倾角β_m就越大。j与β_m近于线性关系。

2）内心距。内心距R_i有着较深的内涵，如果R_i=a₁-b₁为正值，制动过程中，质心C下降，力矩臂e_p缩短，β_m相对减小；而加速过程则完全相反。此外，R_i为正值，各轴偏频n_i是前低于后。一般要求n_n/n₁=1.05～1.15。若R_i=0，则各轴偏频相等。

3）角刚度。角刚度与车身倾角成反比。由公式C_α（β）=∑c_ia_i²可知，要提高角刚度，就得提高换算线刚度c_i和各轴（轮）至中性面的距离a_i。提高c_i将使平顺性变坏。提高角刚度的有效途径在横向上是增大轮距（簧心距）B_i，在纵向上是增大总轴距L，因为它们是平方关系。在L已定的情况下，各中间轴则应远离中性面。例如，独立三轴汽车，其中轴若置于中性面上，则不起抵抗车身纵倾的作用。

在B_i已定的情况下，若各轴内心距R_i=0，且左右悬架换算线刚度均等于c_i，那么角刚度C_αi=C_iB_i²。若R_i≠0，则角刚度

式（3-71）说明，负荷偏置将提高横向角刚度，但这是不可取的。为统一车身稳定性和平顺性这一矛盾，往往通过加装稳定装置来提高角刚度。特别是在空气悬架和那些平顺性要求较高的汽车上，稳定装置的角刚度在总角刚度中占有相当比例。例如林肯轿车约占41%。为有效发挥横向稳定装置的作用，须加大立柱中心距，并使立柱方向与上支点的瞬时速度方向一致。

板簧因自身宽度的抗扭作用，将使横向刚度增加10%～30%。然而，过大的角刚度将使车轴和车身的角频率增加，负荷转移过大，相关零部件载荷增大，轮胎磨损加剧，乃至车轮离地并使平顺性、顺从性和操稳性变坏等。式（3-72）可作为合适角刚度值的检验规范：

C_β≥[（1+j/β_mg）e_p+R_ij/g]P （3-72）

当j=0.4g时，一般可分别取纵倾角β_m≯1.2°，侧倾角α_m≯3.3°。若忽略内心距R_i的影响，角刚度的参考限值为

横向：C_α≮8e_rP （3-73）

纵向：C_β≮20e_pP （3-74）

4）力矩臂。力矩臂e越大，外力矩和车身倾角就越大。由于力矩臂是力矩中心O与簧载质体质心c相对于地面高度的代数差，因此，在c点已定的情况下，O点的位置不仅决定着e值的大小，而且还决定着e值为正、为负或为零。e值为零，倾角为零；e值为负，车身倾斜方向与惯性力方向相反。力矩中心O的位置，完全由悬架设计所决定。

5）侧倾力矩臂。作为二轴汽车，车身系绕着一个共同的侧倾轴线倾斜，而侧倾轴线则是前后悬架力矩中心O₁、O₂的连线，过质心c向地平面所作的垂线与侧倾轴线的交点便是力矩中心O。因此，只要确定了O₁、O₂点，就确定了O点，进而确定了侧倾力矩臂e_r。

作为轴数大于2的多轴汽车，由于各轴力矩中心O_i的高度h_i互不相等，因此就很难找到统一的侧倾轴线。然而，由于各轴侧倾力矩之和∑M_i等于总侧倾力矩M₀，故换算侧倾力矩臂为

式中 P_i——各轴悬架负荷。

由于各轴簧载质量m_i=（1+b_i/R₀）C_ie_im/C。所以(www.xing528.com)

式中 C——整车组合线刚度（N/m），C=∑C_i（1+b_i/R₀）；

R₀——外心矩（m），R₀=∑C_ib_i²/∑C_ib_i；

e_i——各轴侧倾力矩臂（m）。

当某轴侧倾力矩中心高于该轴悬挂质量质心时，其侧倾力矩臂应取负值。在各轴簧载质体质心已定的情况下，e_i的大小决定于O_i点的高低。一般说来，O_i点升高，e_i减小。O_i点不能随意升高。过高在侧向力的作用下，弹簧和车轴等将受到一个较大的力矩。特别当车轮着地点处受到一个侧向力时，冲击易于传递到车身上去。

6）倾覆力矩臂。由于倾覆力矩中心O就是整车约束反力合力N的作用线与中性面的交点，而N又是由各轴悬架导向机构对车身作用力的合力N_i所组成^[1]，因此，只要对N_i按比例采取逐一合成的办法，便可最终确定N的大小和方向。

N力的合成，一般采用作图法，它虽有一定误差，但却直观、迅捷。e_p值的大小除决定于质心高度h_g外，主要决定于悬架“推杆角”ϕ的相位和大小。由于车轴偏离角δ和车身侧倾角α与ϕ之间存在这样的关系：δ=αtgϕ，所以车身稳定性与操纵稳定性总是一对矛盾！

ϕ值的大小和方向，还影响地面冲击的传递、转向盘的摆振、行驶方向的安定、前轮定位参数和传动角度的变化以及制动时车轴和弹簧的受力等，因此应全面考虑！

2.角加速度公式

对人员乘坐和物资运载构成威胁的，主要不是车身倾角β的大小，而是角加速度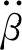的高低。由式（3-70）可知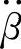，近似于β的线性函数。因此，要降低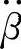，首先就得降低初值a。而a除与加速度j、簧载负荷p和力矩臂e_p成正比外，还与车身对力矩中心O的转动惯量I₀成反比。其次，要降低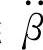，还得降低斜率k。由于C_β远大于Pe_p，所以k是负值。降低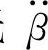的有效措施，除降低簧载负荷G_s和减小力矩臂e_p外，主要是提高角刚度C_β和增大角阻尼k_β。

角阻尼决定于减振器，它虽不影响车身的最大倾角，但对于“点一下”就放开的制动，却因响应滞后而达不到相应加速度j的倾角。特别是能够延缓达到最大倾角的时间。由式（3-66）可知，减振器的布置角度、位置以及阻尼的大小都将影响k_β值。

为充分发挥减振器的效能，其布置方向，作为抵抗车身倾斜，应与上支点的速度方向一致。然而，作为衰减振动的平时工作，又应与下支点的速度方向一致。因此，应综合考虑。

由于r_i值是平方关系，故减振器应布置在车轴相对于中性面的外侧。

增大阻力系数k_i亦能增大k_β，但这是受平顺性对阻尼比的要求所限制的。不过可以采取如下协调措施：由于制动远比加速强烈，故可在不改变周期阻力系数k_i的前提下，在压、拉比λ=k_p/k_r的取值范围内，使中性面前的减振器的压缩阻力系数k_pi和中性面后的减振器的复原阻力系数k_ri相对加大。这样，既可降低制动角加速度，也不致过大地传递地面冲击。

3.力矩中心的位移

在车身倾斜过程中，约束反力合力N的大小和方向时刻都在发生变化，所以力矩中心也在不停地变位。负荷转移、轮胎气压以及制动抱死等都将影响力矩中心的位移，从而使力矩臂、外力矩、角加速度等都在不停地变化，且导致车身最大倾角的改变。力矩中心的位移问题是较为复杂的，只有把β和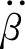的瞬时值记录下来，才能进一步认识其变化规律！