多轴汽车角刚度的影响因素和设计要求

多簧质量系统的角刚度C_θ，系指该系统在外力矩的作用下所产生的反抗力矩M对于角位移θ的变化率，亦即C_θ=dM/dθ。汽车的角刚度是抵抗车身倾斜的重要因素。研究车身稳定性和车身受力状况，必须考虑这一因素。

图3-3是质体绕力矩中心倾斜的力学模型。我们可借助它来建立多簧质量系统角刚度的计算公式。

在图3-3中，C_i为各簧的垂直线刚度，a_i为各簧至中性面的距离。假设质体在外力矩ΔM的作用下，绕中性面上的内心（倾覆力矩中心）转过了一个微元角δθ，各簧变形为δf_i，变形力为δP_i。此时各簧变形力所提供的反抗力矩δM与外力矩ΔM构成平衡，即ΔM=δM=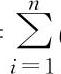C_iai²，加之各簧的变形δf_i=a_iδθ，故按定义便可得到系统角刚度的表达式：

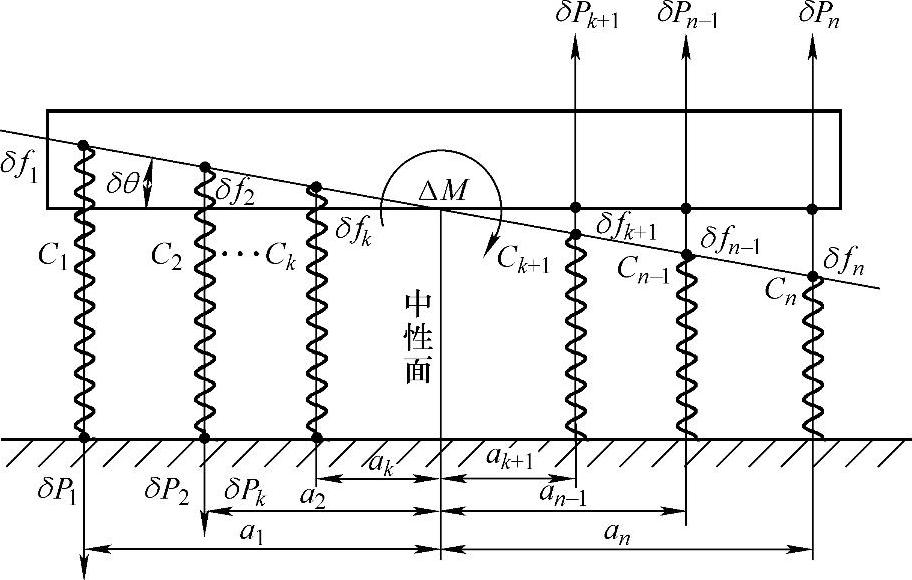
图3-3 质体绕力矩中心倾斜

式中 C_θ——系统角刚度（N·mm/rad）；

C_i——各簧线刚度（N/mm）；

a_i——各簧至中性面的距离（mm）。

当将式（3-17）中的角标作适当变换，并代入式（3-20）且经整理后，可以得到多簧质量系统的角刚度与各簧线刚度及其位置参数的一般关系式：

为了联系多轴汽车的实际和分析的方便，我们令l_n=L，l_i=k_iL，l_j=k_jL。于是式（3-21）变为

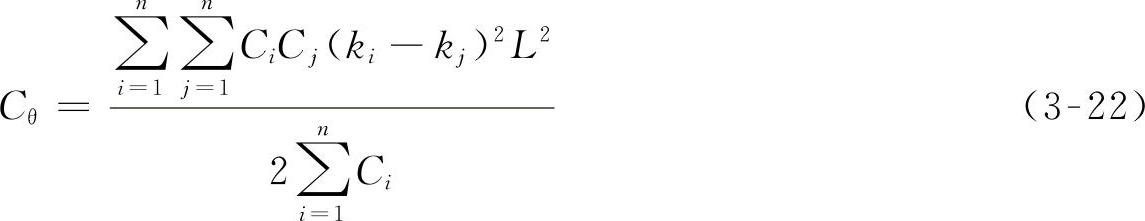
由式（3-22）可知：系统角刚度与各簧的线刚度成正比，与两端弹簧距的平方成正比。对于多轴汽车来说，当总轴距L确定之后，k_i、k_j又是如何影响角刚度值的呢？一般说来，当k_i（k_j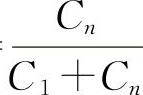）=时，角刚度取得极小值。事实上，当把l_i=k_iL=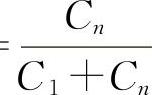代入式（3-17）后，便可得到第i簧至中性面的距离a_i=0。这说明该中间簧的位置与中性面重合，不起抵抗车身倾斜的作用。

例如，当n=3时，角刚度为

C_θ对k₂的一阶导数为

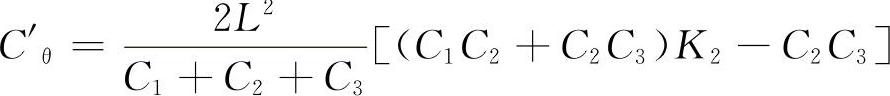
令C＇_θ=0，可解得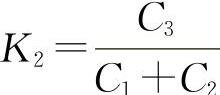。又由于其二阶导数为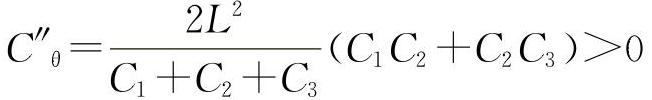所以C_θ在K₂=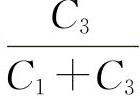有极小值。

由此可知，设计独立三轴汽车时，为使纵向角刚度值增大，当各簧线刚度和总轴距确定之后，中轴位置应适当离开此点。因此时的中性面位置为

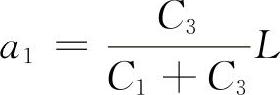
中桥落到了中性面上，弹簧不起抵抗车身倾斜的作用。(www.xing528.com)

式（3-21）既适合计算汽车的纵向角刚度，也适合计算一个车轴的横向角刚度，当把C_θ作为纵向角刚度时，C_i、C_j代表各轴的组合线刚度。例如，当n=2时，若C₁、C₂为前、后轴的组合线刚度，L为轴距，那么，。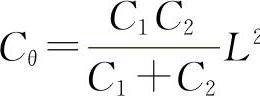

当把C_θ作为横向角刚度时，n只能是2。C_i、C_j即代表左、右悬架的换算组合线刚度。由于左右悬架刚度可以认为相等，于是C_θ=CB²。式中的B，在相关悬架中是弹簧中心距；在独立悬架中，则代表轮距；在横向稳定装置中，应为立柱中心距。整车横向角刚度，应是各轴横向角刚度之和，即C_θ=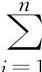C_θi。

在外力矩和力矩臂一定的情况下，要想减少车身的倾角，就得加大角刚度。但过分加大角刚度也是有害的。因为角振动的自然振动频率N_θ=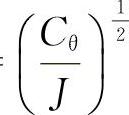。若转动惯量J一定时，增大C_θ值，车身或车轴等角振动频率就将增大，相关零部件的负荷亦将增大。如果是以提高弹簧线刚度的办法来增大角刚度，还将导致平顺性等整车性能的变坏。过大的角刚度，甚至造成转弯时内轮离地和加速轮胎的磨损。

鉴于上述情况，建议汽车角刚度按式（3-23）和式（3-25）取值。

作为整车横向角刚度检验值：

式中 j——侧向加速度（g）；

g——重力加速度；

θ——车身侧倾角（rad）；

P——整车悬挂负荷（N）；

e_s——侧倾力矩臂（mm）。

若按j=0.4g时，θ≤3.3°计算，则有如下近似关系：

C_θT≥8Pe_s （3-24）

作为整车纵向角刚度检验值：

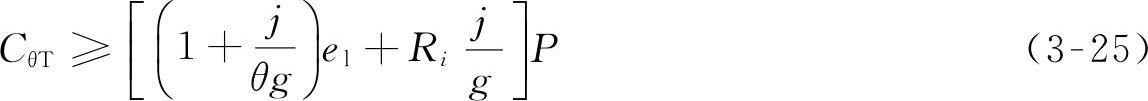
式中 j——纵向加速度（g）；

θ——车身纵倾角（rad）；

e_l——倾覆力矩臂（mm）；

R_i——内心距（mm）。

假若忽略内心距的影响，并按j=0.4g时，θ不大于1.2°计算，便可得如下近似关系：

C_θT≥20e_lP （3-26）